
(1)内角和定理:三角形内角和为 ,这是三角形中三角函数问题的特殊性,解题可不能忘记!任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.锐角三角形
,这是三角形中三角函数问题的特殊性,解题可不能忘记!任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.锐角三角形 三内角都是锐角
三内角都是锐角 三内角的余弦值为正值
三内角的余弦值为正值 任两角和都是钝角
任两角和都是钝角 任意两边的平方和大于第三边的平方.
任意两边的平方和大于第三边的平方.
(2)正弦定理: (R为三角形外接圆的半径).注意:
(R为三角形外接圆的半径).注意:
①正弦定理的一些变式: ;
;

 ;
; ;
;
② 已知三角形两边一对角,求解三角形时,若运用正弦定理,则务必注意可能有两解.
(3)余弦定理: 等,常用余弦定理鉴定三角形形状.
等,常用余弦定理鉴定三角形形状.
(4)面积公式: 等等(其中
等等(其中 为三角形内切圆半径).
为三角形内切圆半径).
(5)三角形中的射影公式: ;
;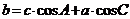 ;
;  .
.
特别提醒:① 求解三角形中的问题时,一定要注意 这个特殊性:
这个特殊性: ;
;
② 求解三角形中含有边角混合关系的问题时,常运用正弦定理、余弦定理实现边角互化。
3.三角恒等式的证明
证明三角恒等式的过程,实际上是化异为同的过程,即化去形式上的异,而呈现实质上的同,这个过程,往往是从化简开始的--这就是说,在证明三角恒等式时,我们可以从最复杂处开始.
例5 求证 cosα(2secα+tgα)(secα-2tgα)=2cosα-3tgα.
分析 从复杂的左边开始证得右边.
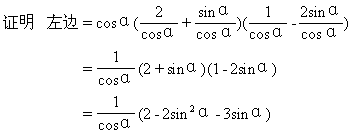

=2cosα-3tgα=右边
例6 证明恒等式
(1)1+3sin2αsec4α+tg6α=sec6α
(2)(sinA+ secA)3+(cosA+cscA)2=(1+secAcscA)2
分析 (1)的左、右两边均较复杂,所以可以从左、右两边同时化简

证明 (1)右边-左边=sec6α-tg6α-3sin2αsec4α-1
=(sec2α-tg2α)(sec4α+sec2α·tg2α+tg2α)-3sin2αsec4α-1
=(sec4α-2sec2αtg2α+tg2α)-1
=(sec2α-tg2α)2-1=0
∴等式成立.

=sin2A+cos2A=1故原式成立
在解题时,要全面地理解“繁”与“简”的关系.实际上,将不同的角化为同角,以减少角的数目,将不同的函数名称,化为同名函数,以减少函数的种类,都是化繁为简,以上两点在三角变换中有着广泛的应用.

分析1 从右端向左端变形,将“切”化为“弦”,以减少函数的种类.


分析2 由1+2sinxcosx立即想到(sinx+cosx)2,进而可以约分,达到化简的目的.


说明 (1)当题目中涉及多种名称的函数时,常常将切、割化为弦(如解法1),或将弦化为切(如解法2)以减少函数的种类.
(2)要熟悉公式的各种变形,以便迅速地找到解题的突破口,请看下列.

=secα+tgα

∴等式成立
说明 以上证明中采用了“1的代换”的技巧,即将1用sec2α-tg2α代换,可是解题者怎么会想到这种代换的呢?很可能,解题者在采用这种代换时,已经预见到代换后,分子可以因式分解,可以约分,而所有这一切都是建立在熟悉公式的各种变形的基础上的,当然,对不熟练的解题者而言,还有如下的“一般证法”--即证明“左边-右边=0”


∴左边=右边
2.三角函数式的化简
三角函数式的化简的结果应满足下述要求:
(1)函数种类尽可能地少.
(2)次数尽可能地低.
(3)项数尽可能地少.
(4)尽可能地不含分母.
(5)尽可能地将根号中的因式移到根号外面来.
化简的总思路是:尽可能地化为同类函数再化简.
例3 化简sin2α·tgα+cos2α·ctgα+2sinαcosα

=secα·cscα
解2 原式=(sin2α·tgα+sinα·cosα)+(cos2α·ctgα+sinαcosα)
=tgα·(sin2α+cos2α)+ctgα(sin2α+cos2α)
=tgα+ctgα

=secα·cscα
说明 (1)在解1中,将正切、余切化为正弦、余弦再化简,仍然是循着减少函数种类的思路进行的.
(2)解2中的逆用公式将sinα·cosα用tgα表示,较为灵活,解1与解2相比,思路更自然,因而更实用.
例4 化简:

分析 将被开方式配成完全平方式,脱去根号,进行化简.



1.已知某角的一个三角函数值,求该角的其他三角函数值.
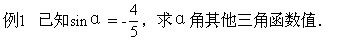
解 ∵sinα<0
∴角α在第三或第四象限(不可能在y轴的负半轴上)

(2)若α在第四象限,则

说明 在解决此类问题时,要注意:
(1)尽可能地确定α所在的象限,以便确定三角函数值的符号.
(2)尽可能地避免使用平方关系(在一般情况下只要使用一次).
(3)必要时进行讨论.
例2 已知sinα=m(|m|≤1),求tgα的值.

(2)当m=±1时,α的终边在y轴上,tgα无意义.
(3)当α在Ⅰ、Ⅳ象限时,∵cosα>0.

当α在第Ⅱ、Ⅲ象限时,∵cosα<0,

说明 (1)在对角的范围进行讨论时,不可遗漏终边在坐标轴上的情况.
(2)本题在进行讨论时,为什么以cosα的符号作为分类的标准,而不按sinα的符号(即m的符号)来分类讨论呢?你能找到这里的原因并概括出所用的技巧吗?
22.如图,已知平面 平行于三棱锥
平行于三棱锥 的底面,等边三角形
的底面,等边三角形 所在平面与面
所在平面与面 垂直,且
垂直,且 ,设
,设 。
。
(1证明: 为异面直线
为异面直线 与
与 的公垂线;
的公垂线;
(2求点 与平面
与平面 的距离;
的距离;
(3求二面角 的大小。
的大小。
高三第一轮复习训练题
21.
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
∠ABC=∠BAD=90°, .
.
(1)求证:平面PAC⊥平面PCD;
(2)在棱PD上是否存在一点E,使CE//平面PAB?
若存在,请确定E点的位置;若不存在,请说明理由
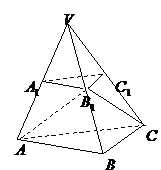
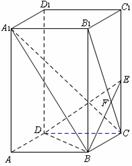
20.如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
⑴求证:A1C⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
19. 如图6所示,在长方体ABCD-A1B1C1D1中,AB = BC = 1,
BB1 = 2,正是棱CC1上的点,且
(1)求三棱锥C-BED的体积;
(2)求证:A1C⊥平面BDE.
.
18.如图,已知DA⊥平面ABE,四边形ABCD是边长为2的正方形,
在△ABE中,AE=1,BE=
(1)证明:平面ADE⊥平面BCE;
(2)求二面角B-AC-E的余弦值。

17. 如图,在四棱锥
如图,在四棱锥 中,
中,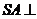 平面
平面 ,
, ,
, ,
, 与平面
与平面 所成角的大小是
所成角的大小是 .
.
 (1)求四棱锥
(1)求四棱锥 的体积;
的体积;
(2)求异面直线 与
与 所成角的大小.
所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com