
例1.求下列三角函数的值
(1) sin240º; (2) ;(3) cos(-252º);(4) sin(-
;(3) cos(-252º);(4) sin(- )
)
解:(1)sin240º=sin(180º+60º)=-sin60º=
(2)  =cos
=cos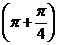 =
= =
= ;
;
(3) cos(-252º)=cos252º= cos(180º+72º)=-cos72º=-0 3090;
3090;
(4) sin(- )=-sin
)=-sin =-sin
=-sin =sin
=sin =
=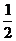
说明:本题是诱导公式二、三的直接应用.通过本题的求解,使学生在利用公式二、三求三角函数的值方面得到基本的、初步的训练.本例中的(3)可使用计算器或查三角函数表.
例2.求下列三角函数的值
(1)sin(-119º45′);(2)cos ;(3)cos(-150º);(4)sin
;(3)cos(-150º);(4)sin

解:(1)sin(-119º45′)=-sin119º45′=-sin(180º-60º15′)
= -sin60º15′=-0 8682
8682
(2)cos =cos(
=cos( )=cos
)=cos =
=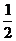
(3)cos(-150º)=cos150º=cos(180º-30º) =-cos30º= ;
;
(4)sin =sin(
=sin(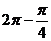 )=-sin
)=-sin =
=

说明:本题是公式四、五的直接应用,通过本题的求解,使学生在利用公式四、五求三角函数的值方面得到基本的、初步的训练.本题中的(1)可使用计算器或查三角函数表.
例3.求值:sin -cos
-cos -sin
-sin
略解:原式=-sin -cos
-cos -sin
-sin
=-sin -cos
-cos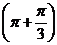 +sin
+sin
=sin +cos
+cos +sin
+sin =
=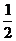 +
+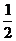 +0
+0 3090=1
3090=1 3090
3090 
说明:本题考查了诱导公式一、二、三的应用,弧度制与角度制的换算,是一道比例1略难的小综合题.利用公式求解时,应注意符号.
例4.求值:sin(-1200º)·cos1290º+cos(-1020º)·sin(-1050º)+tan855º
解:原式=-sin(120º+3·360º)cos(210º+3·360º)
+cos(300º+2·360º)[-sin(330º+2·360º)]+tan(135º+2·360º)
=-sin120º·cos210º-cos300º·sin330º+tan135º
=-sin(180º-60º)·cos(180º+30º)
- cos(360º-60º)·sin(360º-30º)+
=sin60º·cos30º+cos60º·sin30º-tan45º= ·
· +
+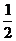 ·
·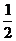 -1=0
-1=0
说明:本题的求解涉及了诱导公式一、二、三、四、五以及同角三角函数的关系.与前面各例比较,更具有综合性.通过本题的求解训练,可使学生进一步熟练诱导公式在求值中的应用.
例5.化简:

略解:原式= =
= =1
=1
说明:化简三角函数式是诱导公式的又一应用,应当熟悉这种题型.
例6.化简:

解:原式=
= =
= =
=

说明:本题可视为例5的姐妹题,相比之下,难度略大于例5.求解时应注意从所涉及的角中分离出2 的整数倍才能利用诱导公式一.
的整数倍才能利用诱导公式一.
例7.求证: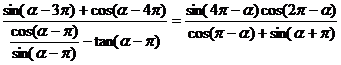
证明:左边= =
=
=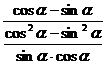 =
=
= ,
,
右边= =
= ,
,
所以,原式成立.
例8.求证
证明:左边=
= =tan3α=右边,
=tan3α=右边,
所以,原式成立.
说明:例7和例8是诱导公式及同角三角函数的基本关系式在证明三角恒等式中的又一应用,具有一定的综合性.尽管问题是以证明的形式出现的,但其本质是等号左、右两边三角式的化简.
例9.已知 .求:
.求: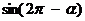 的值.
的值.
解:已知条件即 ,
,
又 ,
,
所以: =
=
说明:本题是在约束条件下三角函数式的求值问题.由于给出了角 的范围,因此,
的范围,因此, 的三角函数的符号是一定的,求解时既要注意诱导公式本身所涉及的符号,又要注意根据
的三角函数的符号是一定的,求解时既要注意诱导公式本身所涉及的符号,又要注意根据 的范围确定三角函数的符号.
的范围确定三角函数的符号.
例10.已知 ,求:
,求:
 的值
的值
解:由 ,得
,得
 ,
,
所以
故

=
=1+tan +2tan2
+2tan2
=1+


说明:本题也是有约束条件的三角函数式的求值问题,但比例9要复杂一些.它对于学生熟练诱导公式及同角三角函数关系式的应用.提高运算能力等都能起到较好的作用.
例11.已知 的值.
的值.
解:因为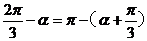 ,
,
所以: =
=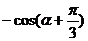 =-m
=-m
由于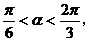 所以
所以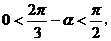
于是: =
= ,
,
所以:tan( =
=

说明:通过观察,获得角 与角
与角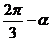 之间的关系式
之间的关系式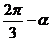 =
= -(
-( ),为顺利利用诱导公式求cos(
),为顺利利用诱导公式求cos(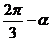 )的值奠定了基础,这是求解本题的关键,我们应当善于引导学生观察,充分挖掘的隐含条件,努力为解决问题寻找突破口,本题求解中一个鲜明的特点是诱导公式中角的结构要由我们通过对已知式和欲求之式中角的观察分析后自己构造出来,在思维和技能上显然都有较高的要求,给我们全新的感觉,它对于培养学生思维能力、创新意识,训练学生素质有着很好的作用.
)的值奠定了基础,这是求解本题的关键,我们应当善于引导学生观察,充分挖掘的隐含条件,努力为解决问题寻找突破口,本题求解中一个鲜明的特点是诱导公式中角的结构要由我们通过对已知式和欲求之式中角的观察分析后自己构造出来,在思维和技能上显然都有较高的要求,给我们全新的感觉,它对于培养学生思维能力、创新意识,训练学生素质有着很好的作用.
例12.已知cos ,角
,角 的终边在y轴的非负半轴上,求cos
的终边在y轴的非负半轴上,求cos 的值.
的值.
解:因为角 的终边在y轴的非负半轴上,
的终边在y轴的非负半轴上,
所以: =
= ,
,
于是 2( )=
)=
从而 
所以  =
= =
= =
=
说明:本题求解中,通过对角 的终边在y轴的非负半轴上的分析而得的
的终边在y轴的非负半轴上的分析而得的 =
= ,还不能马上将未知与已知沟通起来.然而,当我们通过观察,分析角
,还不能马上将未知与已知沟通起来.然而,当我们通过观察,分析角 的结构特征,并将它表示为2(
的结构特征,并将它表示为2( )
) 后,再将
后,再将 =
= 代入,那么未知和已知之间随即架起了一座桥梁,它为利用诱导公式迅速求值扫清了障碍.通过本题的求解训练,对于培养学生的观察分析能力以及思维的灵活性和创造性必将大有裨益.
代入,那么未知和已知之间随即架起了一座桥梁,它为利用诱导公式迅速求值扫清了障碍.通过本题的求解训练,对于培养学生的观察分析能力以及思维的灵活性和创造性必将大有裨益.
诱导公式一(其中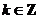 ): 用弧度制可写成
): 用弧度制可写成

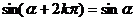




公式二: 用弧度制可表示如下:
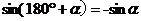




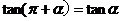
公式三: 


公式四: 用弧度制可表示如下:

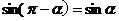




公式五: 用弧度制可表示如下:






(1)不同类型的晶体:一般而言,熔、沸点高低顺序为原子晶体>离子晶体和金属晶体>分子晶体
(2)同类晶体:
①原子晶体的熔、沸点取决于共价键的键长和键能,键长越短、键越大,熔、沸点越高,如金刚石>金刚砂>晶体硅
②离子晶体的熔、沸点取决于离子键的强弱,通常离子半径越小、离子所带电荷数大,离子键越强,熔、沸点高,如KF>KCl>KBr、NaCl>KCl;
晶格能是指 形成1摩离子晶体释放的能量,通常取正值,晶格能越大,形成的离子晶体越 ,且熔沸点
③分子晶体的熔、沸点取决于分子间作用力的大小,通常分子极性越强、相对分子质量越大,分子间作用力越强,熔、沸越高,有氢键的分子晶体,还要考虑氢键的强弱
④同类金属晶体中,金属离子半径越小,阳离子带电荷数越高,金属键越强,熔、沸点越高,如Li>Na>K, Na<Mg<Al
试题枚举
[例1]晶体具有各向异性。如蓝晶石(Al2O3·SiO2)在不同方向上的硬度不同;又如石墨在与层垂直的方向上的导电率与层平行的方向上的导电率1∕104。晶体的各向异性主要表现在是:( )
①硬度 ②导热性 ③导电性 ④光学性质
A.①③ B.②④ C.①②③ D.①②③④
答案:D
[例2]下列属于分子晶体的一组物质是
A. CaO、NO、CO B .CCl4、H2O2、He
C .CO2、SO2、NaCl D .CH4、O2、Na2O
解析:固态金属是金属晶体;大多数的盐、碱和金属氧化物是离子晶体;熟记常见的原子晶体;其它常见物质大多是分子晶体
答案:B。
[例3]下列性质符合分子晶体的是
A . 熔点1070℃,易熔于水,水溶液能导电
B. 熔点是10.31℃,液体不导电,水溶液能导电
C. 熔点97.81℃,质软,能导电,密度是0.97g/cm3
D. 熔点973℃,熔化时能导电,水溶液也能导电
解析:A、D中的物质熔点较高,D中物质熔化时能导电,都是离子化合物;C中物质固态能导电,应为金属单质
答案:B
[例4]下列大小关系正确的是( )
A.晶格能:NaCl<NaBr B.硬度:MgO>CaO
C.熔点:NaI>NaBr D.熔沸点:CO2>NaCl
解析:离子半径 Cl-<Br- 离子键 NaCl>NaBr,晶格能NaCl>NaBr,A项错误;MgO、CaO均为离子晶体,离子半径Mg2+<Ca2+,MgO中离子键强,键能大,晶格能大,硬度大,B正确;C类似;D中CO2分子晶体,NaCl是离子晶体,熔沸点:CO2<NaCl
答案:B
[例5]金属能导电的原因是
A. 金属晶体中金属阳离子与自由电子间的相互作用较弱
B.金属晶体中的自由电子在外加电场作用下可发生定向移动
C.金属晶体中的金属阳离子在外加电场作用下可发生定向移动
D.金属晶体在外加电场作用下可失去电子
解析:金属晶体中金属阳离子与自由电子间的相互作用属于静电作用,是强烈的相互作用,A错误;金属晶体在外加电场作用下电子定向移动,不会失去。
答案:B
[例6]现有甲、乙、丙、丁四种晶胞(如图所示),可推知:甲晶体中A与B的离子个数比为 ;乙晶体的化学式为 ;丙晶体的化学式为______;丁晶体的化学式为______。

解析:立方晶胞体心的微粒一个晶胞所有,面心的微粒为两个晶胞是共有,每个微粒有1/2属于该晶胞,棱边的微粒为4个晶胞共有,每个微粒有1/4属于该晶胞,顶点的微粒为个8晶胞共有,每个微粒有1/8属于该晶胞。
答案:1∶1 C2D EF XY3Z
2.常见晶体的结构
 在金刚石的晶体结构中每个碳原子与周围的4个碳原子形成四个碳碳单键,这5个碳原子形成的是 结构,两个碳碳单键的键角为
,其中的碳原子采取 杂化,金刚石晶体中C原子数与C-C键数之比为 ,晶体中最小的环上上的碳原子数为 ;石墨晶体中C原子数与C-C键数之比为 ;NaCl晶体中Na+的配位数为 ,Cl-的配位数为 ,每个Na+的周围距离最近且相等的Na+的个数为 ,CsCl晶体中Cs+的配位数为 ,Cl-的配位数为 ,每个Cs+的周围距离最近且相等的Cs+的个数为 ;二氧化硅晶体中每个硅原子与 个氧原子相连,在二氧化硅晶体中最小的环中有 个原子,1mol二氧化硅晶体中,Si-O的数目为 。
在金刚石的晶体结构中每个碳原子与周围的4个碳原子形成四个碳碳单键,这5个碳原子形成的是 结构,两个碳碳单键的键角为
,其中的碳原子采取 杂化,金刚石晶体中C原子数与C-C键数之比为 ,晶体中最小的环上上的碳原子数为 ;石墨晶体中C原子数与C-C键数之比为 ;NaCl晶体中Na+的配位数为 ,Cl-的配位数为 ,每个Na+的周围距离最近且相等的Na+的个数为 ,CsCl晶体中Cs+的配位数为 ,Cl-的配位数为 ,每个Cs+的周围距离最近且相等的Cs+的个数为 ;二氧化硅晶体中每个硅原子与 个氧原子相连,在二氧化硅晶体中最小的环中有 个原子,1mol二氧化硅晶体中,Si-O的数目为 。
思考:右图是二氧化硅晶体的一部分,立方体体心的黑点表示一个硅原子,
在图中画出与硅原子相连的氧原子所在的位置。
1.概念:描述 叫做晶胞;整块晶体由晶胞“无隙并置”而成;晶胞①中Ti、O、Ca原子数分别为 、 、 ;晶胞②中A、B、C、D原子数分别为 、 、 、 。



分子晶体中分子间尽可能采用紧密排列方式,分子的排列方式与其形状的关;离子晶体可视为不等径圆球的密堆积,离子晶体中正负离子的配位数主要由正负电荷的 (几何因素)、正负电荷的 (电荷因素)以及离子键的纯粹程度(键性因素)决定;金属晶体的结构可以归结为等径圆球的堆积,可分为Po的简单立方堆积、 型、 型和 型。
(1)晶体是内部微粒(原子、离子、分子)在空间按一定规则做 构成的 物质,晶体区别于非晶体的三个特征是:具有 的几何外形,各向 和具有固定的 。
(2)根据晶体内部微粒的 的微粒间 的不同可以将晶体分为通过离子键形成的 晶体,以金属键基本作用形成的 晶体,通过价键形成的 晶体和通过分子间相互作用形成的 晶体。
(3)常见晶体类型比较:
|
晶体类型 类型 比较 |
分子晶体 |
原子晶体 |
离子晶体 |
金属晶体 |
|
|
构成晶体 微粒 |
|
|
|
|
|
|
形成晶体微粒间作用力 |
|
|
|
|
|
|
作用力大小决定因素 |
|
|
|
|
|
|
物理性质 |
熔沸点 |
|
|
|
|
|
硬度 |
|
|
|
|
|
|
导电性 |
|
|
|
|
|
|
传热性 |
|
|
|
|
|
|
延展性 |
|
|
|
|
|
|
溶解性 |
|
|
|
|
|
|
典型实例 |
P4、干冰、硫 |
金刚石、SiO2 |
NaCl、KOH、NH4Cl |
金属单质 |
7.集合A=N,B={m|m=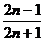 ,n∈N},f:x→y=
,n∈N},f:x→y= ,x∈A,y∈B.请计算在f作用下,象
,x∈A,y∈B.请计算在f作用下,象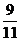 ,
, 的原象分别是多少.( 5,6.)
的原象分别是多少.( 5,6.)
分析:求象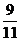 的原象只需解方程
的原象只需解方程 =
=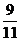 求出x即可.同理可求
求出x即可.同理可求 的原象.
的原象.
6.下面哪一个说法正确?
(A)对于任意两个集合A与B,都可以建立一个从集合A到集合B的映射
(B)对于两个无限集合A与B,一定不能建立一个从集合A到集合B的映射
(C)如果集合A中只有一个元素,B为任一非空集合,那么从集合A到集合B只能建立一个映射
(D)如果集合B只有一个元素,A为任一非空集合,则从集合A到集合B只能建立一个映射
5.在从集合A到集合B的映射中,下列说法哪一个是正确的?
(A)B中的某一个元素b的原象可能不止一个
(B)A中的某一个元素a的象可能不止一个
(C)A中的两个不同元素所对应的象必不相同
(D)B中的两个不同元素的原象可能相同
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com