
11.已知A={x|x2-ax+a2-19=0},B={x|log3(x2+x-3)=1},C={x|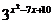 =1},且Æ
=1},且Æ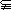 A∩B,A∩C=Æ,求实数a的值
A∩B,A∩C=Æ,求实数a的值
10.已知集合A={x|6/(x+1)³1},B={x|x2-2x+2m<0,xÎR},若AÈB=A,求实数m的取值范围
9.已知集合A={y|y2-(a2+a+1)y+a(a2+1)>0},B={y|y=x2/2-x+5/2,0£x£3},若A∩ B=Æ,求实数a的取值范围
8.设全集I=R,A={x|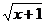 £0},B={x|lg(x2-2)=lgx},求A∩
£0},B={x|lg(x2-2)=lgx},求A∩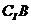

7.若集合A={3-2x,1,3} ,B={1,x2},且AÈ B=A,求实数x
5.设集合A={x|x2+x-1=0},B={x|ax+1=0},若B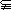 A,则实数a的不同取值个数为
A,则实数a的不同取值个数为 
6 设全集I=R,集合A={x|x2-x-2= -y2,yÎ
R,y≠0},B={y|y=x+1,xÎA},则
设全集I=R,集合A={x|x2-x-2= -y2,yÎ
R,y≠0},B={y|y=x+1,xÎA},则
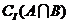 =
= 
4.若{1,2}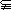 AÍ{1,2,3,4,5}, 则满足这一关系的集合A的个数为
AÍ{1,2,3,4,5}, 则满足这一关系的集合A的个数为 
3.设集合A={x|x2<a} ,B={x|x<2},若A∩ B=A,则实数a的取值范围是( )
(A)a<4 (B)a£4 (C)0<a£4 (D)0<a<4
+(200÷30)=146
所以,符合条件的数共有200-146=54(个)
例6 已知全集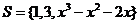 ,A={1,
,A={1,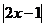 }如果
}如果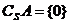 ,则这样的实数
,则这样的实数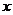 是否存在?若存在,求出
是否存在?若存在,求出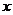 ,若不存在,说明理由
,若不存在,说明理由
分析:此题的关键是理解符号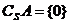 是两层含义:
是两层含义: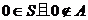
解:∵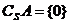 ∴
∴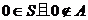 ,即
,即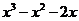 =0,
=0,
解得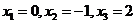
当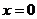 时,
时,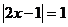 ,为A中元素
,为A中元素
当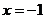 时,
时,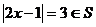
当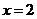 时,
时,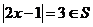
∴这样的实数x存在,是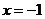 或
或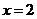

另法:∵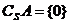 ∴
∴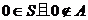 ,
,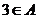
∴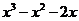 =0且
=0且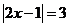
∴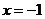 或
或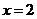

变式思考题:
同时满足条件:①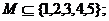 ②若
②若 ,这样的集合M有多少个,举出这些集合来
,这样的集合M有多少个,举出这些集合来
答案:这样的集合M有8个:
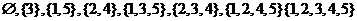

例7 某学校艺术班有100名学生,其中学舞蹈的学生67人,学唱歌的学生45人,而学乐器的学生既不能学舞蹈,又不能学唱歌,人数是21人,那么同时学舞蹈和唱歌的学生有多少人?
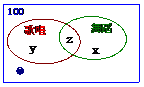 解:设学舞蹈的学生有x人,学唱歌的人有y人,
解:设学舞蹈的学生有x人,学唱歌的人有y人,
既学舞蹈又学唱歌的人又z人,
由题意可列方程:
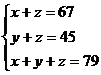 解得
解得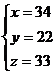
所以,同时学舞蹈和唱歌的有33人
例8对于集合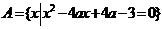 ,
,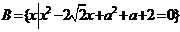 是否存在实数
是否存在实数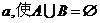 ?若存在,求出
?若存在,求出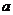 的取值,若不存在,试说明理由
的取值,若不存在,试说明理由
解: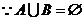 ∴
∴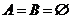 , 即二次方程:
, 即二次方程:
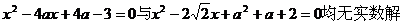 ,
,
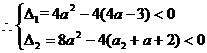 ,解之得
,解之得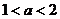
故存在实数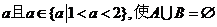

例9已知集合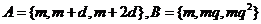 ,
,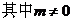 ,
,
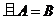 ,求
,求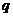 的值
的值
解:由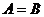 可知,
可知,
(1)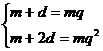 ,或(2)
,或(2)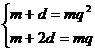
解(1)得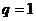 ,
,
解(2)得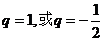
又因为当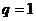 时,
时,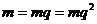 与题意不符
与题意不符
所以,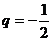

例10已知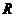 为全集,
为全集,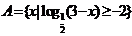 ,
,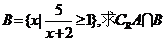

解:由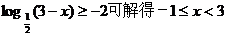
所以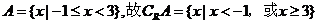
由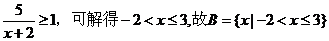
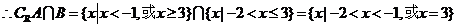
例11已知集合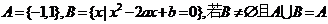 ,求
,求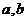 的值
的值
解: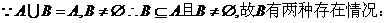
(1)当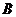 含有两个元素时:
含有两个元素时: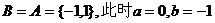 ;
;
(2)当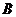 含有一个元素时:
含有一个元素时: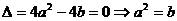
若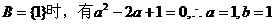
若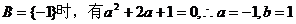
综上可知: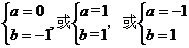

小结:
1 正确理解集合中元素的特征:确定性,互异性,无序性;
正确理解集合中元素的特征:确定性,互异性,无序性;
2 用列举法或描述法给出集合,考察元素与集合之间的元素;或不给出集合中的元素,但只给出若干个抽象的集合及某些关系,运用文氏图解决有关问题
用列举法或描述法给出集合,考察元素与集合之间的元素;或不给出集合中的元素,但只给出若干个抽象的集合及某些关系,运用文氏图解决有关问题
3 熟练运用集合的并、交、补的运算并进行有关集合的运算
熟练运用集合的并、交、补的运算并进行有关集合的运算
4 注意符号的理解,相互之间的转化:例如
注意符号的理解,相互之间的转化:例如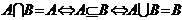 等等
等等
学生练习
题组一:
1 已知集合M={x|x2<4},N={x|x2-2x-3<0},则集合M∩N等于
已知集合M={x|x2<4},N={x|x2-2x-3<0},则集合M∩N等于
A {x|x<-2} B
{x|x<-2} B {x|x>3}
C
{x|x>3}
C {x|-1<x<2}
D
{x|-1<x<2}
D {x|2<x<3}
{x|2<x<3}
解析:M={x|x2<4}={x|-2<x<2},
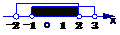 N={x|x2-2x-3<0}={x|-1<x<3},结合数轴,
N={x|x2-2x-3<0}={x|-1<x<3},结合数轴,
∴M∩N={x|-1<x<2}
答案:C
2 已知集合A={x∈R|x<5-
已知集合A={x∈R|x<5-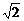 },B={1,2,3,4},则(
},B={1,2,3,4},则(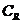 A)∩B等于
A)∩B等于
A {1,2,3,4}
B
{1,2,3,4}
B {2,3,4} C
{2,3,4} C {3,4} D
{3,4} D {4}
{4}
解析: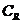 A={x∈R|x≥5-
A={x∈R|x≥5-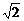 },而5-
},而5-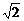 ∈(3,4),
∈(3,4),
∴(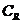 A)∩B={4}
A)∩B={4}
答案:D
3 设集合P={1,2,3,4,5,6},Q={x∈R|2≤x≤6},那么下列结论正确的是
设集合P={1,2,3,4,5,6},Q={x∈R|2≤x≤6},那么下列结论正确的是
A P∩Q=P B
P∩Q=P B P∩Q
P∩Q Q C
Q C P∪Q=Q D
P∪Q=Q D P∩Q
P∩Q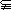 P
P
解析:P∩Q={2,3,4,5,6},∴P∩Q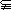 P
P
答案:D
4 设U是全集,非空集合P、Q满足P
设U是全集,非空集合P、Q满足P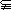 Q
Q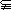 U,若求含P、Q的一个集合运算表达式,使运算结果为空集
U,若求含P、Q的一个集合运算表达式,使运算结果为空集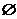 ,则这个运算表达式可以是______
,则这个运算表达式可以是______
解析:构造满足条件的集合,实例论证
U={1,2,3},P={1},Q={1,2},
则(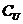 Q)={3},(
Q)={3},(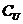 P)={2,3},易见(
P)={2,3},易见(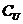 Q)∩P=
Q)∩P=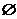

答案:(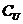 Q)∩P
Q)∩P
5 已知集合A={0,1},B={x|x∈A,x∈N*},C={x|x
已知集合A={0,1},B={x|x∈A,x∈N*},C={x|x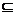 A},则A、B、C之间的关系是________
A},则A、B、C之间的关系是________
解析:用列举法表示出B={1},C={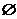 ,{1},{0},A},易见其关系
,{1},{0},A},易见其关系 这里A、B、C是不同层次的集合,C以A的子集为元素,同一层次的集合可有包含关系,不同层次的集合之间只能是从属关系
这里A、B、C是不同层次的集合,C以A的子集为元素,同一层次的集合可有包含关系,不同层次的集合之间只能是从属关系
答案:B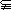 A,A∈C,B∈C
A,A∈C,B∈C
题组二:
1 设全集为实数集R,集合M={x|x2-1999x-2000>0},P={x||x-1999|<a}(a为常数),且-1ÎP,则M与P满足
( )
设全集为实数集R,集合M={x|x2-1999x-2000>0},P={x||x-1999|<a}(a为常数),且-1ÎP,则M与P满足
( )
(A)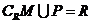 (B)
(B)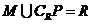
(C)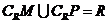 (D)
(D)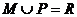
2.若非空集合A={x|2a+1£x£3a-5},B={x|3£x£22},则能使AÍB
成立的所有a的集合是( )
(A){a|1£a£9} (B){a|6£a£9} (C){a|a£9} (D)Æ
(A)根据要求完成小作文,词数:30词左右。(5分)
假如你叫Rick,你的朋友Edward送给你一件你非常喜欢的礼物,请你写一封短小的
感谢信。
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
(B)根据要求完成大作文,词数:60-80词。(15分)
三年的学习生活就要结束了,在这几年的英语(或语文、数学……)学习中,你一定积累
了不少的学习经验。请选择-个学科,写一篇短文,谈谈你对该学科的学习经验和感受。
要求:字迹工整,语言连贯。文中不得出现真实姓名和所在学校的相关信息。
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com