
 物理情形:地球和太阳的质量分别为m和M ,地球绕太阳作椭圆运动,轨道的半长轴为a ,半短轴为b ,如图11所示。试求地球在椭圆顶点A、B、C三点的运动速度,以及轨迹在A、C两点的曲率半径。
物理情形:地球和太阳的质量分别为m和M ,地球绕太阳作椭圆运动,轨道的半长轴为a ,半短轴为b ,如图11所示。试求地球在椭圆顶点A、B、C三点的运动速度,以及轨迹在A、C两点的曲率半径。
模型分析:求解天体运动的本来模式,常常要用到开普勒定律(定量)、机械能守恒(万有引力势能)、椭圆的数学常识等等,相对高考要求有很大的不同。
地球轨道的离心率很小(其值 ≈0.0167 ,其中c为半焦距),这是我们常常能将它近似为圆的原因。为了方便说明问题,在图11中,我们将离心率夸大了。
≈0.0167 ,其中c为半焦距),这是我们常常能将它近似为圆的原因。为了方便说明问题,在图11中,我们将离心率夸大了。
针对地球从A点运动到B点的过程,机械能守恒
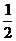 m
m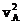 +(-
+(- )=
)= 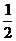 m
m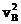 +(-
+(- )
)
比较A、B两点,应用开普勒第二定律,有:vA(a-c)= vB(a + c)
结合椭圆的基本关系:c = 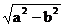
解以上三式可得:vA = 
 , vB
=
, vB
= 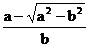

再针对地球从A到C的过程,应用机械能守恒定律,有
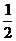 m
m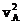 +(-
+(- )=
)= 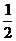 m
m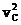 +(-
+(- )
)
代入vA值可解得:vC = 
为求A、C两点的曲率半径,在A、C两点建自然坐标,然后应用动力学(法向)方程。
在A点,F万 = ΣFn = m an ,设轨迹在A点的曲率半径为ρA ,即:G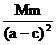 = m
= m
 代入vA值可解得:ρA =
代入vA值可解得:ρA = 
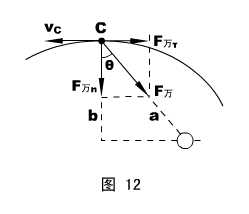
在C点,方程复杂一些,须将万有引力在τ、n方向分解,如图12所示。
然后,F万n =ΣFn = m an ,即:F万cosθ= m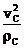
即:G ·
·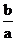 = m
= m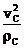
代入vC值可解得:ρC = 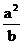
值得注意的是,如果针对A、C两点用开普勒第二定律,由于C点处的矢径r和瞬时速度vC不垂直,方程不能写作vA(a-c)= vC a 。
正确的做法是:将vC分解出垂直于矢径的分量(分解方式可参看图12,但分解的平行四边形未画出)vC cosθ,再用vA(a-c)=(vC cosθ)a ,化简之后的形式成为
vA(a-c)= vC b
要理解这个关系,有一定的难度,所以建议最好不要对A、C两点用开普勒第二定律
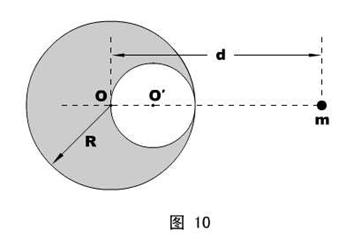 物理情形:如图9所示,半径为R的均质球质量为M,球心在O点,现在被内切的挖去了一个半径为R/2的球形空腔(球心在O′)。在O、O′的连线上距离O点为d的地方放有一个很小的、质量为m的物体,试求这两个物体之间的万有引力。
物理情形:如图9所示,半径为R的均质球质量为M,球心在O点,现在被内切的挖去了一个半径为R/2的球形空腔(球心在O′)。在O、O′的连线上距离O点为d的地方放有一个很小的、质量为m的物体,试求这两个物体之间的万有引力。
模型分析:无论是“基本条件”还是“拓展条件”,本模型都很难直接符合,因此必须使用一些特殊的处理方法。本模型除了照应万有引力的拓展条件之外,着重介绍“填补法”的应用。
空腔里现在虽然空无一物,但可以看成是两个半径为R/2的球的叠加:一个的质量为+M/8 ,一个的质量为-M/8 。然后,前者正好填补空腔--和被挖除后剩下的部分构成一个完整的均质球A ;注意后者,虽然是一个比较特殊的物体(质量为负值),但仍然是一个均质的球体,命名为B 。
既然A、B两物均为均质球体,他们各自和右边小物体之间的万有引力,就可以使用“拓展条件”中的定势来计算了。只是有一点需要说明,B物的质量既然负值,它和m之间的万有“引力”在方向上不再表现为吸引,而应为排斥--成了“万有斥力”了。具体过程如下
FAm = G
FBm = G = -G
= -G
最后,两物之间的万有引力 F = FAm
+ FBm = G -G
-G
需要指出的是,在一部分同学的心目中,可能还会存在另一种解题思路,那就是先通过力矩平衡求被挖除物体的重心(仍然要用到“填补法”、负质量物体的重力反向等),它将在O、O′的连线上距离O点左侧R/14处,然后“一步到位”地求被挖除物与m的万有引力
F = G
然而,这种求法违背了万有引力定律适用的条件,是一种错误的思路。
 物理情形:如图8所示,长为L的细绳一端固定,另一端系一小球。当小球在最低点时,给球一个vo = 2
物理情形:如图8所示,长为L的细绳一端固定,另一端系一小球。当小球在最低点时,给球一个vo = 2 的水平初速,试求所能到达的最大高度。
的水平初速,试求所能到达的最大高度。
模型分析:用自然坐标分析变速圆周运动的典型事例。能量关系的运用,也是对常规知识的复习。
(学生活动)小球能否形成的往复的摆动?小球能否到达圆弧的最高点C ?
通过能量关系和圆周运动动力学知识的复习,得出:小球运动超过B点、但不能到达C点(vC ≥ ),即小球必然在BC之间的某点脱离圆弧。
),即小球必然在BC之间的某点脱离圆弧。
(学生活动)小球会不会在BC之间的某点脱离圆弧后作自由落体运动?
尽管对于本问题,能量分析是可行的(BC之间不可能出现动能为零的点,则小球脱离圆弧的初速度vD不可能为零),但用动力学的工具分析,是本模型的重点--
 在BC阶段,只要小球还在圆弧上,其受力分析必如图9所示。沿轨迹的切向、法向分别建τ、n坐标,然后将重力G沿τ、n分解为Gτ和Gn分量,T为绳子张力。法向动力学方程为
在BC阶段,只要小球还在圆弧上,其受力分析必如图9所示。沿轨迹的切向、法向分别建τ、n坐标,然后将重力G沿τ、n分解为Gτ和Gn分量,T为绳子张力。法向动力学方程为
T + Gn = ΣFn = man = m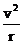
由于T≥0 ,Gn>0 ,故v≠0 。(学生活动:若换一个v0值,在AB阶段,v = 0是可能出现的;若将绳子换成轻杆,在BC阶段v = 0也是可能出现的。)
下面先解脱离点的具体位置。设脱离点为D,对应方位角为θ,如图8所示。由于在D点之后绳子就要弯曲,则此时绳子的张力T为零,而此时仍然在作圆周运动,故动力学方程仍满足
Gn = Gsinθ= m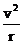 ①
①
在再针对A→D过程,小球机械能守恒,即(选A所在的平面为参考平面):
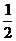 m
m + 0 = mg ( L + Lsinθ) +
+ 0 = mg ( L + Lsinθ) +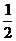 m
m ②
②
代入v0值解①、②两式得:θ= arcsin ,(同时得到:vD =
,(同时得到:vD = 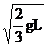 )小球脱离D点后将以vD为初速度作斜向上抛运动。它所能到达的最高点(相对A)可以用两种方法求得。
)小球脱离D点后将以vD为初速度作斜向上抛运动。它所能到达的最高点(相对A)可以用两种方法求得。
解法一:运动学途径。
先求小球斜抛的最大高度,hm
=  =
= 
代入θ和vD的值得:hm = 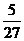 L
L
小球相对A的总高度:Hm = L + Lsinθ+ hm =  L
L
解法二:能量途径
小球在斜抛的最高点仍具有vD的水平分量,即vDsinθ= 
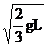 。对A→最高点的过程用机械能守恒定律(设A所在的平面为参考平面),有
。对A→最高点的过程用机械能守恒定律(设A所在的平面为参考平面),有
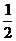 m
m + 0 =
+ 0 =  + mg Hm
+ mg Hm
容易得到:Hm =  L
L
物理情形:不计空气阻力,将小球斜向上抛出,初速度大小恒为v0 ,方向可以选择,试求小球落回原高度的最大水平位移(射程)。
模型分析:斜抛运动的常规分析和平抛运动完全相同。
设初速度方向与水平面夹θ角,建立水平、竖直的x、y轴,将运动学参量沿x、y分解。针对抛出到落回原高度的过程
0 = Sy = v0y t + 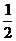 (-g)t2
(-g)t2
Sx = v0x t
解以上两式易得:Sx =  sin2θ
sin2θ
结论:当抛射角θ= 45°时,最大射程Sxmax = 
(学生活动)若v0 、θ确定,试用两种方法求小球到达的最大高度。
运动学求解--考查竖直分运动即可;能量求解--注意小球在最高点应具备的速度v0x ,然后对抛出到最高点的过程用动能定理或机械能守恒。结论:Hm =  。
。
物理情形:如图5所示,岸边的汽车用一根不可伸长的轻绳通过定滑轮牵引水中的小船,设小船始终不离开水面,且绳足够长,求汽车速度v1和小船速度v2的大小关系。
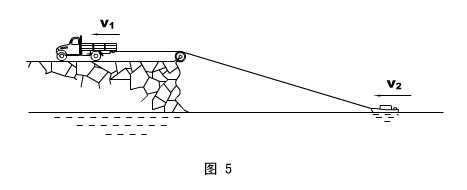 模型分析:由于绳不可伸长,滑轮右边绳子缩短的速率即是汽车速度的大小v1 ,考查绳与船相连的端点运动情况,v1和v2必有一个运动的合成与分解的问题。
模型分析:由于绳不可伸长,滑轮右边绳子缩短的速率即是汽车速度的大小v1 ,考查绳与船相连的端点运动情况,v1和v2必有一个运动的合成与分解的问题。
(学生活动)如果v1恒定不变,v2会恒定吗?若恒定,说明理由;若变化,定性判断变化趋势。
结合学生的想法,介绍极限外推的思想:当船离岸无穷远时,绳与水的夹角趋于零,v2→v1 。当船比较靠岸时,可作图比较船的移动距离、绳子的缩短长度,得到v2>v1 。故“船速增大”才是正确结论。
故只能引入瞬时方位角θ,看v1和v2的瞬时关系。
(学生活动)v1和v2定量关系若何?是否可以考虑用运动的分解与合成的知识解答?
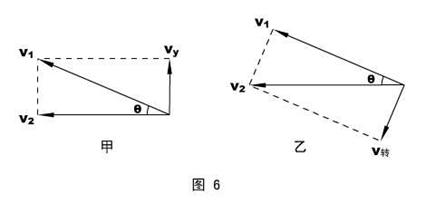
针对如图6所示的两种典型方案,初步评说--甲图中v2 = v1cosθ,船越靠岸,θ越大,v2越小,和前面的定性结论冲突,必然是错误的。
错误的根源分析:和试验修订本教材中“飞机起飞”的运动分析进行了不恰当地联系。仔细比较这两个运动的差别,并联系“小船渡河”的运动合成等事例,总结出这样的规律--
 合运动是显性的、轨迹实在的运动,分运动是隐性的、需要分析而具有人为特征(无唯一性)的运动。
合运动是显性的、轨迹实在的运动,分运动是隐性的、需要分析而具有人为特征(无唯一性)的运动。
解法一:在图6(乙)中,当我们挖掘、分析了滑轮绳子端点的运动后,不难得出:船的沿水面运动是v2合运动,端点参与绳子的缩短运动v1和随绳子的转动v转 ,从而肯定乙方案是正确的。
即:v2 = v1
/ cosθ
解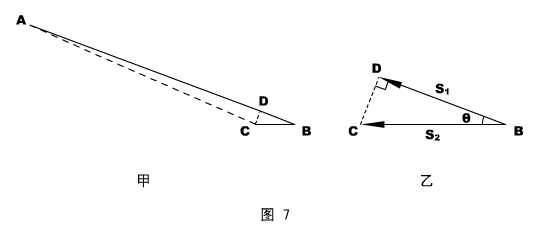 法二:微元法。从考查位置开始取一个极短过程,将绳的运动和船的运动在图7(甲)中标示出来,AB是绳的初识位置,AC是绳的末位置,在AB上取
法二:微元法。从考查位置开始取一个极短过程,将绳的运动和船的运动在图7(甲)中标示出来,AB是绳的初识位置,AC是绳的末位置,在AB上取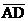 =
=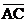 得D点,并连接CD。显然,图中BC是船的位移大小,DB是绳子的缩短长度。由于过程极短,等腰三角形ACD的顶角∠A→0,则底角∠ACD→90°,△CDB趋于直角三角形。将此三角放大成图7(乙),得出:S2 = S1
/ cosθ 。
得D点,并连接CD。显然,图中BC是船的位移大小,DB是绳子的缩短长度。由于过程极短,等腰三角形ACD的顶角∠A→0,则底角∠ACD→90°,△CDB趋于直角三角形。将此三角放大成图7(乙),得出:S2 = S1
/ cosθ 。
鉴于过程极短,绳的缩短运动和船的运动都可以认为是匀速的,即:S2 = v2 t ,S1 = v1 t 。
所以:v2 = v1 / cosθ
2、求渡河的位移和最小位移
在上面的讨论中,小船的位移事实上已经得出,即
S合 =  =
= 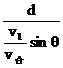 =
= 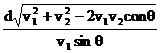

但S合(θ)函数比较复杂,寻求S合的极小值并非易事。因此,我们可以从其它方面作一些努力。
将S合沿x、y方向分解成Sx和Sy ,因为Sy ≡ d ,要S合极小,只要Sx极小就行了。而Sx(θ)函数可以这样求--
解法一: Sx = vxt
=(v2 - v1x) =(v2 – v1cosθ)
=(v2 – v1cosθ)

为求极值,令cosθ= p ,则sinθ=  ,再将上式两边平方、整理,得到
,再将上式两边平方、整理,得到


这是一个关于p的一元二次方程,要p有解,须满足Δ≥0 ,即
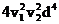 ≥
≥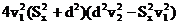

整理得 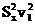 ≥
≥

所以,Sxmin=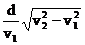 ,代入Sx(θ)函数可知,此时cosθ=
,代入Sx(θ)函数可知,此时cosθ= 

最后,Smin=  =
= 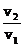 d
d
此过程仍然比较繁复,且数学味太浓。结论得出后,我们还不难发现一个问题:当v2<v1时,Smin<d ,这显然与事实不符。(造成这个局面的原因是:在以上的运算过程中,方程两边的平方和开方过程中必然出现了增根或遗根的现象)所以,此法给人一种玄乎的感觉。
解法二:纯物理解--矢量三角形的动态分析
从图2可知,Sy恒定,Sx越小,必有S合矢量与下游河岸的夹角越大,亦即v合矢量与下游河岸的夹角越大(但不得大于90°)。
我们可以通过v1与v2合成v合矢量图探讨v合与下游河岸夹角的最大可能。
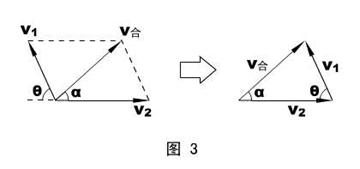
先进行平行四边形到三角形的变换,如图3所示。
当θ变化时,v合矢量的大小和方向随之变化,具体情况如图4所示。

从图4不难看出,只有当v合和虚线半圆周相切时,v合与v2(下游)的夹角才会最大。此时,v合⊥v1 ,v1、v2和v合构成一个直角三角形,αmax = arcsin

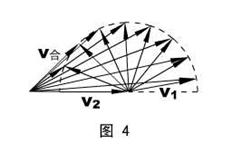
 并且,此时:θ= arccos
并且,此时:θ= arccos

有了αmax的值,结合图1可以求出:S合min = 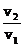 d
d
最后解决v2<v1时结果不切实际的问题。从图4可以看出,当v2<v1时,v合不可能和虚线半圆周相切(或αmax = arcsin 无解),结合实际情况,αmax取90°
无解),结合实际情况,αmax取90°
即:v2<v1时,S合min = d ,此时,θ= arccos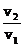

结论:若v1<v2 ,θ= arccos 时,S合min =
时,S合min = 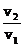 d
d
若v2<v1 ,θ= arccos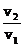 时,S合min = d
时,S合min = d
物理情形:在宽度为d的河中,水流速度v2恒定。岸边有一艘小船,保持相对河水恒定的速率v1渡河,但船头的方向可以选择。试求小船渡河的最短时间和最小位移。
模型分析:小船渡河的实际运动(相对河岸的运动)由船相对水流速度v1和水相对河岸的速度v2合成。可以设船头与河岸上游夹角为θ(即v1的方向),速度矢量合成如图1
(学生活动)用余弦定理可求v合的大小
v合=

(学生活动)用正弦定理可求v合的方向。令v合与河岸下游夹角为α,则
α= arcsin

1、求渡河的时间与最短时间
 由于合运动合分运动具有等时性,故渡河时间既可以根据合运动求,也可以根据分运动去求。针对这一思想,有以下两种解法
由于合运动合分运动具有等时性,故渡河时间既可以根据合运动求,也可以根据分运动去求。针对这一思想,有以下两种解法
解法一: t = 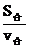

其中v合可用正弦定理表达,故有 t = 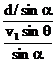 =
= 

解 法二: t =
法二: t =  =
= 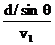 =
= 

此外,结合静力学正交分解的思想,我们也可以建立沿河岸合垂直河岸的坐标x、y,然后先将v1分解(v2无需分解),再合成,如图2所示。而且不难看出,合运动在x、y方向的分量vx和vy与v1在x、y方向的分量v1x、v1y以及v2具有以下关系
vy = v1y
vx = v2 - v1x
由于合运动沿y方向的分量Sy ≡ d ,故有
解法三: t =  =
= 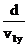 =
= 

t (θ)函数既已得出,我们不难得出结论
当θ= 90°时,渡河时间的最小值 tmin = 

(从“解法三”我们最容易理解t为什么与v2无关,故tmin也与v2无关。这个结论是意味深长的。)
3、解天体运动的本来模式时,应了解椭圆的数学常识
第二讲 重要模型与专题

2、从能量角度求第二、第三宇宙速度
万有引力势能EP = -G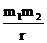

1、第一宇宙速度的常规求法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com