
6.证明:若a > 0,则
§5.4不等式的应用
5.若x > 1,y > 1,求证:
4.若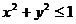 ,求证:
,求证: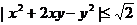
3.已知x > 0 , y > 0,2x + y = 1,求证: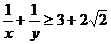
2.已知a,b,c,d都是正数,求证:
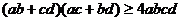
1.比较(a+3)(a-5)与(a+2)(a-4)的大小.
[例1] 已知a>b(ab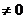 ),比较
),比较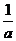 与
与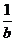 的大小.
的大小.
错解: a>b(ab
a>b(ab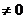 ),
),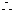
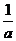 <
<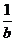 .
.
错因:简单的认为大数的倒数必定小,小数的倒数必定大.正确的结论是:当两数同号时,大数的倒数必定小,小数的倒数必定大.
正解: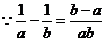 ,又
,又 a>b(ab
a>b(ab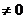 ),
),
(1)当a、b同号时,即a>b>0或b<a<0时,则ab>0,b-a<0, 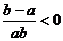 ,
,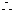
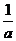 <
<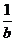 .
.
(2)当a、b异号时,则a>0,b<0, 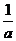 >0,
>0,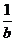 <0
<0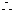
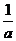 >
>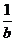 .
.
[例2] 当a、b为两个不相等的正实数时,下列各式中最小的是( )
A.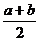 B.
B.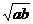 C.
C.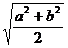 D.
D.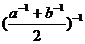
错解:所以选B.
错因是由于在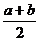 、
、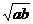 、
、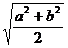 中很容易确定
中很容易确定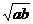 最小,所以易误选B.而事实上三者中最小者,并不一定是四者中最小者,要得到正确的结论,就需要全面比较,不可遗漏
最小,所以易误选B.而事实上三者中最小者,并不一定是四者中最小者,要得到正确的结论,就需要全面比较,不可遗漏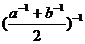 与前三者的大小比较.
与前三者的大小比较.
正解:由均值不等式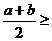
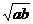 及a2+b2
及a2+b2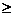 2ab,可知选项A、B、C中,
2ab,可知选项A、B、C中,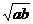 最小,而
最小,而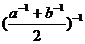 =
= ,由当a
,由当a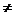 b时,a+b>2
b时,a+b>2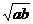 ,两端同乘以
,两端同乘以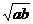 ,可得(a+b)·
,可得(a+b)·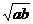 >2ab,
>2ab,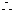
 <
<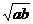 ,因此选D.
,因此选D.
[例3] 已知:a>0 , b>0 , a+b=1,求(a+ )2+(b+ )2的最小值.
错解: (a+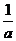 )2+(b+
)2+(b+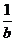 )2=a2+b2+
)2=a2+b2+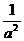 +
+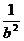 +4≥2ab+
+4≥2ab+ +4≥4
+4≥4 +4=8,
+4=8,
∴(a+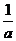 )2+(b+
)2+(b+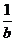 )2的最小值是8.
)2的最小值是8.
错因:上面的解答中,两次用到了基本不等式a2+b2≥2ab,第一次等号成立的条件是a=b= ,第二次等号成立的条件是ab=
,第二次等号成立的条件是ab=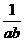 ,显然,这两个条件是不能同时成立的.因此,8不是最小值.
,显然,这两个条件是不能同时成立的.因此,8不是最小值.
正解:原式= a2+b2+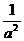 +
+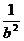 +4=( a2+b2)+(
+4=( a2+b2)+(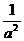 +
+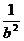 )+4=[(a+b)2-2ab]+[(
)+4=[(a+b)2-2ab]+[(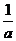 +
+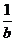 )2-
)2- ]+4
]+4
=
(1-2ab)(1+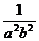 )+4,
)+4,
由ab≤(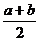 )2=
)2= 得:1-2ab≥1-
得:1-2ab≥1- =
= , 且
, 且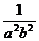 ≥16,1+
≥16,1+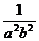 ≥17,
≥17,
∴原式≥ ×17+4=
×17+4=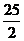 (当且仅当a=b=
(当且仅当a=b= 时,等号成立),
时,等号成立),
∴(a + 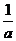 )2 + (b +
)2 + (b + 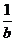 )2的最小值是.
)2的最小值是.
[例4] 已知0 < x < 1, 0 < a < 1,试比较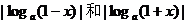 的大小.
的大小.
解法一:
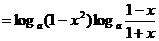
∵0
< 1 - x2 < 1, 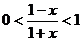 ∴
∴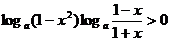
∴
解法二:
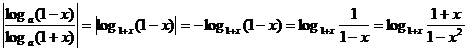

∵0
< 1 - x2 < 1, 1 + x
> 1, ∴
∴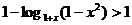 ∴
∴
解法三:∵0 < x < 1, ∴0 < 1 - x < 1, 1 < 1 + x < 2,
∴
∴左 - 右
= 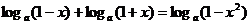
∵0
< 1 - x2 < 1, 且0
< a < 1 ∴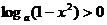
∴
[例5]已知x2 = a2 + b2,y2 = c2 + d2,且所有字母均为正,求证:xy≥ac + bd
证:证法一(分析法)∵a, b, c, d, x, y都是正数
∴要证:xy≥ac + bd
只需证:(xy)2≥(ac + bd)2
即:(a2 + b2)(c2 + d2)≥a2c2 + b2d2 + 2abcd
展开得:a2c2 + b2d2 + a2d2 + b2c2≥a2c2 + b2d2 + 2abcd
即:a2d2 + b2c2≥2abcd 由基本不等式,显然成立
∴xy≥ac + bd
证法二(综合法)xy =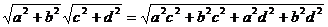
≥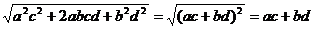
证法三(三角代换法)
∵x2 = a2 + b2,∴不妨设a = xsina, b = xcosa
y2 = c2 + d2 c = ysinb, d = ycosb
∴ac + bd = xysinasinb + xycosacosb = xycos(a - b)≤xy
[例6] 已知x > 0,求证: 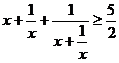
证:构造函数 则
则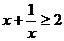 , 设2≤a<b
, 设2≤a<b
由
显然 ∵2≤a<b ∴a - b > 0, ab - 1 > 0, ab > 0 ∴上式 > 0
∴f (x)在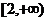 上单调递增,∴左边
上单调递增,∴左边
5.在三角换元中,由于已知条件的限制作用,可能对引入的角有一定的限制,应引起高度重视,否则可能会出现错误的结果.这是换元法的重点,也是难点,且要注意整体思想的应用.
4.反证法证明不等式时,必须要将命题结论的反面的各种情形一一加以导出矛盾.
3.分析法证明过程中的每一步不一定“步步可逆”,也没有必要要求“步步可逆”,因为这时仅需寻找充分条件,而不是充要条件.如果非要“步步可逆”,则限制了分析法解决问题的范围,使得分析法只能使用于证明等价命题了.用分析法证明问题时,一定要恰当地用好“要证”、“只需证”、“即证”、“也即证”等词语.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com