
3.平面内有两定点 上,求一点P使
上,求一点P使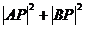 取得最大值或最小值,并求出最大值和最小值.
取得最大值或最小值,并求出最大值和最小值.
2.已知点(-2,3)与抛物线y2=2px(p>0)的焦点 的距离是5,则p= .
1. 设双曲线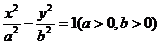 两焦点为F1、F2,点Q为双曲线上除顶点外的任一点,过F1作∠F1QF2的平分线的垂线,垂足为P,则点P的轨迹是 ( )
两焦点为F1、F2,点Q为双曲线上除顶点外的任一点,过F1作∠F1QF2的平分线的垂线,垂足为P,则点P的轨迹是 ( )
A.椭圆的一部分 B.双曲线的一部分
C.抛物线的一部分 D.圆的一部分.
[例1]设双曲线的渐近线为: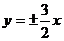 ,求其离心率.
,求其离心率.
错解:由双曲线的渐近线为: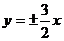 ,可得:
,可得: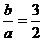 ,从而
,从而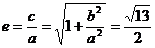
剖析:由双曲线的渐近线为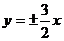 是不能确定焦点的位置在x轴上的,当焦点的位置在y轴上时,
是不能确定焦点的位置在x轴上的,当焦点的位置在y轴上时,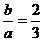 ,故本题应有两解,即:
,故本题应有两解,即:
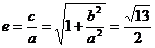 或
或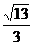 .
.
[例2]设点P(x,y)在椭圆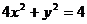 上,求
上,求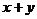 的最大、最小值.
的最大、最小值.
错解:因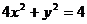 ∴
∴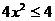 ,得:
,得: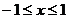 ,同理得:
,同理得: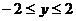 ,故
,故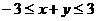 ∴最大、最小值分别为3,-3.
∴最大、最小值分别为3,-3.
剖析:本题中x、y除了分别满足以上条件外,还受制约条件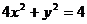 的约束.当x=1时,y此时取不到最大值2,故x+y的最大值不为3.其实本题只需令
的约束.当x=1时,y此时取不到最大值2,故x+y的最大值不为3.其实本题只需令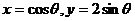 ,则
,则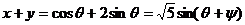 ,故其最大值为
,故其最大值为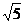 ,最小值为
,最小值为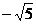 .
.
[例3]已知双曲线的右准线为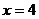 ,右焦点
,右焦点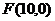 ,离心率
,离心率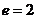 ,求双曲线方程.
,求双曲线方程.
错解一: 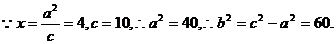 故所求的双曲线方程为
故所求的双曲线方程为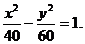
错解二:
由焦点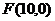 知
知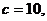

故所求的双曲线方程为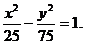
错因: 这两个解法都是误认为双曲线的中心在原点,而题中并没有告诉中心在原点这个条件。由于判断错误,而造成解法错误。随意增加、遗漏题设条件,都会产生错误解法.
解法一:
设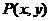 为双曲线上任意一点,因为双曲线的右准线为
为双曲线上任意一点,因为双曲线的右准线为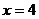 ,右焦点
,右焦点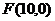 ,离心率
,离心率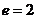 ,由双曲线的定义知
,由双曲线的定义知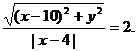 整理得
整理得 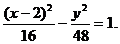
解法二: 依题意,设双曲线的中心为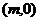 ,
,
则 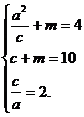 解得
解得 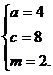 ,所以
,所以 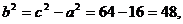
故所求双曲线方程为 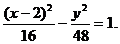
[例4]设椭圆的中心是坐标原点,长轴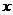 在轴上,离心率
在轴上,离心率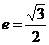 ,已知点
,已知点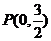 到这个椭圆上的最远距离是
到这个椭圆上的最远距离是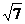 ,求这个椭圆的方程.
,求这个椭圆的方程.
错解:依题意可设椭圆方程为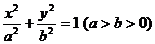
则 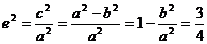 ,
,
所以 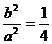 ,即
,即 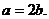
设椭圆上的点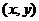 到点
到点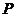 的距离为
的距离为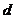 ,
,
则 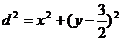
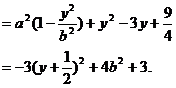
所以当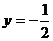 时,
时,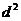 有最大值,从而
有最大值,从而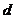 也有最大值。
也有最大值。
所以 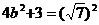 ,由此解得:
,由此解得:
于是所求椭圆的方程为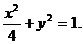
错因:尽管上面解法的最后结果是正确的,但这种解法却是错误的。结果正确只是碰巧而已。由当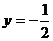 时,
时,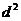 有最大值,这步推理是错误的,没有考虑
有最大值,这步推理是错误的,没有考虑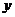 到的取值范围.事实上,由于点
到的取值范围.事实上,由于点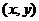 在椭圆上,所以有
在椭圆上,所以有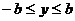 ,因此在求
,因此在求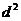 的最大值时,应分类讨论.
的最大值时,应分类讨论.
正解:若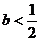 ,则当
,则当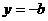 时,
时,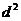 (从而
(从而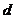 )有最大值.
)有最大值.
于是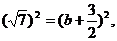 从而解得
从而解得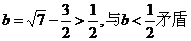 .
.
所以必有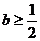 ,此时当
,此时当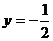 时,
时,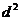 (从而
(从而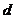 )有最大值,
)有最大值,
所以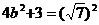 ,解得
,解得
于是所求椭圆的方程为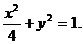
[例5]从椭圆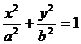 ,(
,(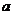 >b>0)上一点M向x轴所作垂线恰好通过椭圆的左焦点F1,A、B分别是椭圆长、短轴的端点,AB∥OM.设Q是椭圆上任意一点,当QF2⊥AB时,延长QF2与椭圆交于另一点P,若⊿F1PQ的面积为20
>b>0)上一点M向x轴所作垂线恰好通过椭圆的左焦点F1,A、B分别是椭圆长、短轴的端点,AB∥OM.设Q是椭圆上任意一点,当QF2⊥AB时,延长QF2与椭圆交于另一点P,若⊿F1PQ的面积为20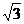 ,求此时椭圆的方程.
,求此时椭圆的方程.
解:本题可用待定系数法求解.
∵b=c, 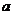 =
=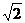 c,可设椭圆方程为
c,可设椭圆方程为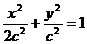 .
.
∵PQ⊥AB,∴kPQ=-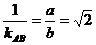 ,则PQ的方程为y=
,则PQ的方程为y=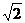 (x-c),
(x-c),
代入椭圆方程整理得5x2-8cx+2c2=0,
根据弦长公式,得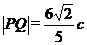 ,
,
又点F1到PQ的距离d=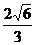 c
c
∴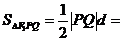
 ,由
,由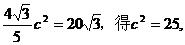
故所求椭圆方程为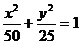 .
.
[例6]已知椭圆: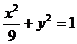 ,过左焦点F作倾斜角为
,过左焦点F作倾斜角为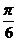 的直线交椭圆于A、B两点,求弦AB的长.
的直线交椭圆于A、B两点,求弦AB的长.
解:a=3,b=1,c=2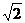 ; 则F(-2
; 则F(-2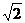 ,0)
,0)
由题意知: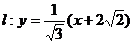 与
与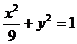 联立消去y得:
联立消去y得:
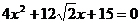
设A(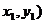 、B(
、B(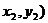 ,则
,则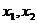 是上面方程的二实根,由违达定理,
是上面方程的二实根,由违达定理,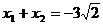
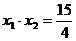 ,
,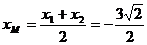 又因为A、B、F都是直线
又因为A、B、F都是直线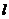 上的点,
上的点,
所以|AB|=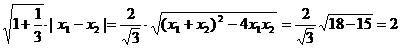
点评:也可利用“焦半径”公式计算.
[例7](06年全国理科)设P是椭圆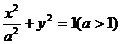 短轴的一个端点,Q为椭圆上的一个动点,求|PQ|的最大值.
短轴的一个端点,Q为椭圆上的一个动点,求|PQ|的最大值.
解: 依题意可设P(0,1),Q(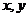 ),则|PQ|=
),则|PQ|=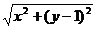 ,又因为Q在椭圆上,所以,
,又因为Q在椭圆上,所以, ,|PQ|2=
,|PQ|2=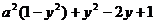 =
=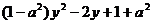
=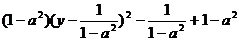 .
.
因为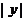 ≤1,
≤1,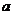 >1,若
>1,若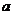 ≥
≥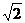 ,则
,则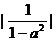 ≤1,当
≤1,当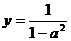 时,|PQ|取最大值
时,|PQ|取最大值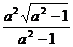 ;若1<
;若1<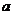 <
<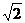 ,则当
,则当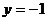 时,|PQ|取最大值2.
时,|PQ|取最大值2.
[例8]已知双曲线的中心在原点,过右焦点F(2,0)作斜率为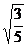 的直线,交双曲线于M、N 两点,且
的直线,交双曲线于M、N 两点,且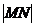 =4,求双曲线方程.
=4,求双曲线方程.
解:设所求双曲线方程为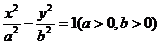 ,由右焦点为(2,0).知C=2,b2=4-
,由右焦点为(2,0).知C=2,b2=4-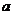 2
2
则双曲线方程为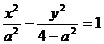 ,设直线MN的方程为:
,设直线MN的方程为: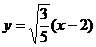 ,代入双曲线方程整理得:(20-8
,代入双曲线方程整理得:(20-8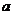 2)x2+12
2)x2+12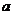 2x+5
2x+5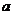 4-32
4-32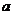 2=0
2=0
设M(x1,y1),N(x2,y2),则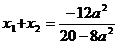 ,
,
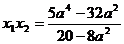 .
.
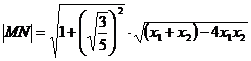
解得 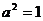 ,
,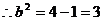 .
.
故所求双曲线方程为: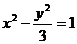 .
.
点评:利用待定系数法求曲线方程,运用一元二次方程的根与系数关系将两根之和与积整体代入,体现了数学的整体思想,也简化了计算,要求学生熟练掌握.
19.抛物线的焦半径公式:
抛物线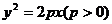 ,
,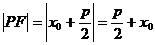
抛物线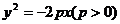 ,
,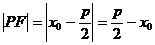
抛物线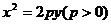 ,
,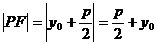
抛物线 ,
,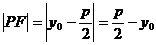
4.抛物线的几何性质
(1)范围
因为p>0,由方程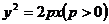 可知,这条抛物线上的点M的坐标(x,y)满足不等式x≥0,所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
可知,这条抛物线上的点M的坐标(x,y)满足不等式x≥0,所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸.
(2)对称性
以-y代y,方程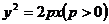 不变,所以这条抛物线关于x轴对称,我们把抛物线的对称轴叫做抛物线的轴.
不变,所以这条抛物线关于x轴对称,我们把抛物线的对称轴叫做抛物线的轴.
(3)顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程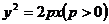 中,当y=0时,x=0,因此抛物线
中,当y=0时,x=0,因此抛物线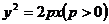 的顶点就是坐标原点.
的顶点就是坐标原点.
(4)离心率
抛物线上的点M与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e表示.由抛物线的定义可知,e=1.
3.共轭双曲线
以已知双曲线的实轴为虚轴,虚轴为实轴,这样得到的双曲线称为原双曲线的共轭双曲线. 双曲线和它的共轭双曲线的焦点在同一圆上. 确定双曲线的共轭双曲线的方法:将1变为-1.
2.共渐近线的双曲线系
如果已知一双曲线的渐近线方程为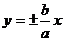
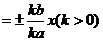 ,那么此双曲线方程就一定是:
,那么此双曲线方程就一定是: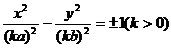 或写成
或写成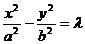 .
.
椭圆、双曲线、抛物线同属于圆锥曲线,它们的定义、标准方程及其推导过程以及简单的几何性质都存在着相似之处,也有着一定的区别,因此,要准确地理解和掌握三种曲线的特点以及它们之间的区别与联系
1.等轴双曲线
定义:实轴和虚轴等长的双曲线叫做等轴双曲线,这样的双曲线叫做等轴双曲线. 等轴双曲线的性质:(1)渐近线方程为: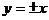 ;(2)渐近线互相垂直;(3)离心率
;(2)渐近线互相垂直;(3)离心率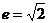 .
.
13. 抛物线定义:
平面内与一个定点F和一条定直线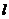 的距离相等的点的轨迹叫做抛物线. 定点F叫做抛物线的焦点,定直线
的距离相等的点的轨迹叫做抛物线. 定点F叫做抛物线的焦点,定直线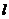 叫做抛物线的准线.
叫做抛物线的准线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com