设物体的质量为m，在恒力F作用下，通过位移为S，其速度由v₀变为v_t，

　则：根据牛顿第二定律F=ma……①　　 根据运动学公式2as=v_t²一v₀²……②

由①②得：FS=½mv_t²－½mv₀²

7．对动能定理中的位移与速度必须相对同一参照物．

6．动能定理的表达式是在物体受恒力作用且做直线运动的情况下得出的．但它也适用于变为及物体作曲线运动的情况．即动能定理对恒力、变力做功都适用；直线运动与曲线运动也均适用．

5．力的独立作用原理使我们有了牛顿第二定律、动量定理、动量守恒定律的分量表达式．但动能定理是标量式．功和动能都是标量，不能利用矢量法则分解．故动能定理无分量式．在处理一些问题时，可在某一方向应用动能定理．

4．各力位移相同时，可求合外力做的功，各力位移不同时，分别求力做功，然后求代数和．

3、动能定理适用单个物体，对于物体系统尤其是具有相对运动的物体系统不能盲目的应用动能定理．由于此时内力的功也可引起物体动能向其他形式能(比如内能)的转化．在动能定理中．总功指各外力对物体做功的代数和．这里我们所说的外力包括重力、弹力、摩擦力、电场力等．　　

2．“增量”是末动能减初动能．ΔE_K＞0表示动能增加，ΔE_K＜0表示动能减小．

做功可以改变物体的能量．所有外力对物体做的总功等于物体动能的增量． W₁+W₂+W₃+……＝½mv_t²－½mv₀²

1．反映了物体动能的变化与引起变化的原因--力对物体所做功之间的因果关系．可以理解为外力对物体做功等于物体动能增加，物体克服外力做功等于物体动能的减小．所以正功是加号，负功是减号。

4、实际问题中的功率

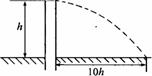[例8]推动节水工程的转动喷水“龙头”。如图所示，龙头距地面h，其喷灌半径可达10h，每分钟喷水质量为m，所用水从地面下H的井中抽取，设水以相同的速率喷出，水泵的效率为η，水泵的功率P至少多大？

解析:水泵对水做功，用来增大水的重力势能和动能．

设水喷出时速度为v，则h=½gt²,10h=vt;解得

每分钟内水泵对水做的功W＝mg(H+h)+½mv²=mg(H+26h)，又W=ηPt,∴

[例9]一传送带装置示意如图，其中传送带经过AB区域时是水平的，经过BC区域时变为圆弧形(圆弧由光滑模板形成，未画出)，经过CD区域时是倾斜的，AB和CD都与BC相切。现将大量的质量均为m的小箱一个一个在A处放到传送带上，放置时初速为零，经传送带运送到D处，D和A的高度差为h。稳定工作时传送带速度不变，CD段上各箱等距排列，相邻两箱的距离为L。每个箱子在A处投上后，在到达B之前已经相对于传送带静止，且以后也不再滑动(忽略经BC段时的微小滑动)。己知在一段相当长的时间T内，共运送小货箱的数目为N，这装置由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦。求电动机的平均输出功率P。

[解析]以地面为参考(下同)，设传送带的运动速度为v₀，在水平段运输的过程中，小货箱先在滑动摩擦力作用下做匀加速运动，设这段路程为S，所用时间为t，加速度为a，则对小箱有：S＝½at²……①

　 v₀＝at………②。在这段时间内，传送带运动的路程为：S₀= v₀t……③，由以上可得S₀＝2S……④。用f表示小箱与传送带之间的滑动摩擦力，则传送带对小箱做功为：W₁=fS=½mv₀²……⑤；传送带克服小箱对它的摩擦力做功：W₀=Fs₀=2·½mv₀²……⑥

两者之差就是克服摩擦力做功发出的热量：Q=½mv₀²……⑦

可见，在小箱加速运动过程中，小箱获得的动能与发热量相等。

T时间内，电动机输出的功为：W=PT……⑧

此功用于增加小箱的动能、势能以及克服摩擦力发热,即W=½Nmv₀²十Nmgh+NQ……⑨

已知相邻两小箱的距离为L，所以：v₀T＝NL……⑩

联立⑦⑧⑨⑩得。

散　　　　　 　动能　 动能定理

知识简析一、动能

　　 如果一个物体能对外做功，我们就说这个物体具有能量．物体由于运动而具有的能．　 E_k＝½mv²，其大小与参照系的选取有关．动能是描述物体运动状态的物理量．是相对量。

3、汽车起动问题分析

(1)当以恒定功率运动时，做加速度越来越小的变加速直线运动，a=－，当F_牵＝f时，加速度a＝0，此时的速度为最大速度．所以v_m=p/f，以后机车做匀速直线运动。

(2)欲使汽车从静止开始做匀加速直线运动，一开始不能用额定功率，功率必须随着速度增加而增加，使P/v=F恒定；这种运动持续一段时间后．汽车又做加速度越来越小的加速运动，最后达到最大速度v_m，所以求匀加速直线运动的时间不可用t=v_m/a，必须用v=P_额/F　 ，而t=v/a，　　 由此得：t= P_额/Fa

[例7]质量为lkg的机械与平面间摩擦力f=2N，其额定功率为12 W，要使它以a＝lm／s²的加速度做匀加速直线运动，问做这种运动的最长时间为多少？

　　 错解：v_m＝P/f＝6m／s，　　　　 t=v_m/a=6s

　 解析：以上做法错在何处，我们进行如下的分析：要使a＝lm／s²，必须F＝f+ma＝3N

要使F=3N速度最大为v=P/F=4m／s　　 所以做匀加速直线运动的时间为t=v/a=4s

这里可做这样的检验：当速度大于4m／s 时，不妨设为5 m／s ；F=P/v=2．4N，则加速度a=(F－f)/m=0．4 m／s²，显然不是匀加速直线运动了，所以一旦速度大于4m／s 时，由于功率不再增加，加速度则变小，做的是加速度越来越小的加速直线运动，直到加速度为零，之后做匀速运动．答案：4 s

点评(1)此类问题关键是发动机的功率是否达到额定功率，若在额定功率下起动，则一定是交加速运动，因为牵引力随速度的增大而减小．求解时不能用匀变速运动的规律来解．具体变化过程可用如下示意图表示．

　　 (2)特别注意匀加速起动时，牵引力恒定．当功率随速度增至预定功率时的速度(匀加速结束时的速度)，并不是车行的最大速度．此后，车仍要在额定功率下做加速度减小的加速运动．(这阶段类同于额定功率起动)直至a=0时速度达到最大．具体变化过程可用如下示意图

[例]一辆汽车在平直的公路上以速度v₀开始加速行驶，经过一段时间t，前进了距离s，此时恰好达到其最大速度V_m.设此过程中汽车发动机始终以额定功率P工作，汽车所受的阻力恒定为F，则在这段时间里，发动机所做的功为(　　 )

A、Fv_mt；B、Pt；C、½mv_m²+Fs－½mv₀²；D、；

解析：汽车在恒定功率作用做变牵引力的加速运动，所以发动机做功为变力做功，根据P=W/t可求得W=Pt，而P=F^/v=Fv_m，所以W= Fv_m t；根据能量守恒：W+½mv₀²=½mv_m²+Fs

所以W=½mv_m²+Fs－½mv₀²；答案：ABC

思考：为何用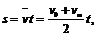得到不正确？错在哪里？

[例]质量为m = 4000kg的卡车，额定输出功率为P=60 kW。当它从静止出发沿坡路前进时，每行驶100 m，升高5m，所受阻力大小为车重的0.1倍，取g=10 m/s² .

试求：(1)卡车能否保持牵引力为8000 N不变在坡路上行驶？

(2)卡车在坡路上行驶时能达到的最大速度为多大？这时牵引力为多大？

(3)如果卡车用4000 N牵引力以12m/s的初速度上坡，到达坡顶时，速度为4 m/s,那么卡车在这一段路程中的最大功率为多少？平均功率是多少？

分析:汽车能否保持牵引力为8000 N上坡要考虑两点：第一，牵引力是否大于阻力？第二，汽车若一直加速，其功率是否将超过额定功率，依P=Fv解。本题考查了汽车牵引力恒定时功率的计算。不少同学在得到F > f + mgsinθ后，立即做出结论：汽车可以保持牵引力8000 N不变上坡；而没有考虑到汽车由于加速，速度不断增大，其功率不断增大，如果坡路足够长，这种运动方式是不允许的。

解：分析汽车上坡过程中受力情况如图所示：牵引力F,重力mg＝4×10⁴N，f＝kmg＝4×10³ N，支持力N，依题意sinθ＝5/100。

(1)汽车上坡时，若F＝8000N,而f+mgsinθ＝4×10³+4×10⁴×1/20＝6×10³ N,即F> f +mgsinθ,汽车将加速上坡，速度不断增大，其输出功率P=Fv也不断增大，长时间后，将超出其额定输出功率，所以，汽车不能保持牵引力为8000N不变上坡。

　(2)汽车上坡时，速度越来越大，必须不断减小牵引力以保证输出功率不超过额定输出功率，当牵引力F= f + mgsinθ=6×10³ N时，汽车加速度为零，速度增大到最大，设为v_m，则P＝Fv＝(f+mgsinθ)·v_m；

F= f + mgsinθ=6×10³ N

(3)若牵引力F=4000N，汽车上坡时，速度不断减小，所以最初的功率即为最大，P=Fv=4000×12=48×10³w。整个过程中平均功率为=32×10³W