4、函数：(1)定义(传统)：如果在某变化过程中有两个变量x,y并且对于x在某个范围内的每一个确定的值，按照某个对应法则，y都有唯一确定的值和它对应，那么y就是x的函数，x叫做自变量，x的取值范围叫做函数的定义域，和x的值对应的y的值叫做函数值，函数值的集合叫做函数的值域。(2)函数的集合定义：设A，B都是非空的数的集合，f：x→y是从A到B的映射，那么，从A到B的f：A→B，叫做A到B的函数，y=f(x),其中x∈A,y∈B,原像集合A叫做函数f(x)的定义域，像集合C叫做函数f(x)的值域。像集合CB

3、映射f：A→B的特征：(1)存在性：集合A中任一元素在集合B中都有像，(2)惟一性：集合A中的任一元素在集合B中的像只有一个，(3)方向性：从A到B的映射与从B到A的映射一般是不一样的(4)集合B中的元素在集合A中不一定有原象，若集合B中元素在集合A中有原像，原像不一定惟一。

2、像与原像：如果给定一个集合A到集合B的映射，那么，和集合A中的a对应的集合B中的b叫做a的像，a叫做b的原像。

1、映射的定义：设A，B是两个集合，如果按照某种对应关系f,对集合A中的任何一个元素，在集合B中都有唯一的元素和它对应，那么，这样的对应叫做集合A到集合B的映射，记作：f：A→B，

22.(本小题满分12分)

　　　 如图，四面体ABCD中，O、E分别是BD、BC的中点，

　　　 (1)求证：平面BCD；

　　　 (2)求异面直线AB与CD所成角的大小；

　　　 (3)求点E到平面ACD的距离。

高三第一轮复习训练题

21． 如图，平面PAD⊥平面ABCD，ABCD为正方形，

△PAD是直角三角形，且PA=AD=2，E、F、G分别是

线段PA、PD、CD的中点.

　 (1)求证：EFG⊥平面PAB；

　 (2)求异面直线EG与BD所成的角；

20．如图，△ABC和△DBC所在平面互相垂直，且AB＝BC＝BD，∠ABC＝∠DBC＝120º，求：⑴A、D连线和平面DBC所成的角；⑵二面角A-BD-C的正切值。

19. 如图，在四棱锥中，四边形为正方形，点在平面内的射影为，且，为中点．

(1)证明：//平面；

(2)证明：平面平面；

(3)求二面角的正切值．

18．在三棱锥M-ABC中，CM⊥平面ABC，MA=MB，NA=NB=NC.

　 (1)求证：AM⊥BC；

　 (1)若∠AMB=60°，求直线AM与CN所成的角.

17. 如图，正三棱柱ABC－A₁B₁C₁的各棱长都等于2，D在AC₁上，F为BB₁中点，且FD⊥AC₁。

　　　 (1)试求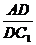的值；

　 　　 (2)求二面角F－AC₁－C的大小；

　　 (3)求点C₁到平面AFC的距离.