3、分数指数幂的定义：(1)

(2)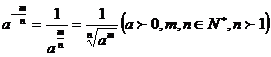，(3)0的正分数指数幂等于0,0的负分数指数幂没有意义。

2、n次方根的性质：(1)0的n次方根是0。即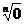＝0(n>1,n∈N)，(2)＝a(n∈N)

(3)当n为奇数时，＝a,　 当n为偶数时, ＝|a|

1、n次方根的定义：如果一个数的n次方a(n>1,n∈N)那么这个数叫做a的n次方根，即x=a,则x叫做a的n次方根(n>1,n∈N)。

3、翻折变换：(1)由y=f(x)得到y=|f(x)|，就是把y=f(x)的图象在x轴下方的部分作关于x轴对称的图象，即把x轴下方的部分翻到x轴上方，而原来x轴上方的部分不变。

(2) 由y=f(x)得到y=f(|x|)，就是把y=f(x)的图象在y轴右边的部分作关于y轴对称的图象，即把y轴右边的部分翻到y轴的左边，而原来y轴左边的部分去掉，右边的部分不变。

第五讲 指数函数、对数函数与幂函数

2、伸缩变换：将y=f(x)的横坐标变为原来的a倍，纵坐标变为原来的m倍，得到

即

1、平移变换(向量平移法则)：y=f(x)按＝(h,k)平移得y=f(x－h)+k,即F(x,y)=0按＝(h,k)平移得F(x－h,y－k)=0,当m>0时,向右平移，m<0时,向左平移。当n>0时,向上平移，n<0时向下平移。对于“从y=f(x)到y=f(x－h)+k”是“左加右减，上加下减”，对于平移向量“＝(h,k)”是“左负右正，上正下负”。

5、若f(a+x)=f(b-x)，则f(x)的图像关于直线对称，

三：图象平移与伸缩变换、翻折变换。

4、类似4有y=f(x)关于直线y=－x+b对称时, f(x)＝b－f(b－x)。特别当b＝0时，f(x)＝－f(－x), f(x)关于直线y=－x对称.

3、y=f(x)关于直线y=x+b对称时,由上面知y=f(x)关于直线y=x+b对称的函数的解析式是y=f(x+b)+b。它与y=f(x)应是同一函数，所以：f(x)＝f(x+b)+b。特别当b＝0时，f(x)＝f(x)，即一个函数关于直线y=x对称时，它的反函数就是它本身。

2、y=f(x)关于(a,b)对称时,f(x)=2b－f(2a－x)，特别a=b=0时， f(x)=－f(－x)，即f(x)关于原点对称，f(x)为奇函数。