
1、幂函数的定义
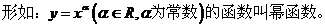
4、对数有关的大小比较:(1)类似指数函数分为四类: 1)同底且大于1,真数大的对数大。2)同底且小于1,真数大的对数小。 3)同真数且大于1,在x轴同侧时,底大图低,(这一点与指数函数相反)4)同真数且小于1,在x轴同侧时,底大图高。(2)基本思路:1)利用函数的单调性,2)作差或作商法,3)利用中间量。4)化同底或化同指数。5)放缩法。
3、对数函数y=log x (a>0,a≠1)与指数函数y=a
x (a>0,a≠1)与指数函数y=a (a>0,a≠1)互为反函数,它们的定义域与值域正好互换,它们的对应法则是互逆的,其图象关于y=x对称。
(a>0,a≠1)互为反函数,它们的定义域与值域正好互换,它们的对应法则是互逆的,其图象关于y=x对称。
2、对数函数的图象与性质:
|
|
a>1 |
0<a<1 |
|
|
图象 |
  
|
|


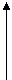 性质
性质 x
x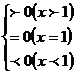
 x
x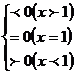
1、定义:形如y=log x (a>0,a≠1)的函数叫做对数函数。
x (a>0,a≠1)的函数叫做对数函数。
3、对数的恒等式:
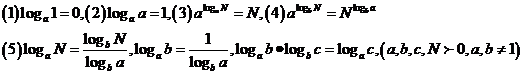
2、对数的运算性质:

1、对数的定义:如果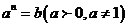 ,那么b叫做以a为底N的对数,记做
,那么b叫做以a为底N的对数,记做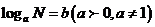 ,由定义知负数和0没有对数。通常以10为底的对数叫做常用对数,记做
,由定义知负数和0没有对数。通常以10为底的对数叫做常用对数,记做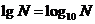 。以无理数e=2.71828…为底的对数叫做自然对数。记做
。以无理数e=2.71828…为底的对数叫做自然对数。记做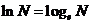 。
。
2、指数函数y=a (a>0,且a≠1)的图象和性质:
(a>0,且a≠1)的图象和性质:
|
|
a>1 |
0<a<1 |
|
|
|
图象 |
   |
  
|

性质
(1)
定义域:R 值域: (0,+∞)
(2)
都过点 (0,1) (1,a)
(3)
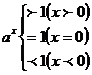
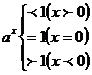
(4)
在R上是增函数
在R上是减函数
1、定义:形如y=a (a>0,且a≠1)的函数叫做指数函数。
(a>0,且a≠1)的函数叫做指数函数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com