4、等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等。当一边平行且方向相同而另一边的方向相反时，这两个角互补。可推广到空间：如果一个二面角的两个半平面和另一个二面角的两个半平面分别平行并且方向相同，那么这两个二面角相等。当一个半平面平行且方向相同而另一个半平面的方向相反时，这两个二面角互补。

但注意：如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补。不可推广到空间：如果一个二面角的两个半平面和另一个二面角的两个半平面分别垂直，那么这两个二面角相等或互补。

3、平行公理：平行于同一直线的两直线互相平行，它反应了平行线的传递性。注意：相交线和异面直线没有传递性。

2、点、线、面的位置关系的表示方法。

1、确定平面的4个公理或定理，(1)不共线的3点确定一个平面，(2)两条相交直线确定一个平面，(3)两条平行直线确定一个平面，(4)一条直线和直线外一点确定一个平面。

确定直线在平面内的定理：如果直线上有两个点在平面内，则直线在平面内。

两个平面的公共点的个数定理：如果两个平面有一个公共点，则必有无数个公共点，且这些公共点的个数在同一条直线上。此定理常用来判断空间三线共点。

2、三视图与直观图的画法。

1)、直观图的画法(斜二侧画法规则)：已知图形中平行于横轴和竖轴的线段，在直观图中保持长度不变，平行于纵轴的线段，在直观图中其长度为原来的一半。原来平行的线段仍然平行，原来相交的线段仍然相交，但角度可能发生变化。把直观图还原成原来水平放置的图形时，应先把与横轴成45的线段还原成与横轴成直角的线段。

2)、三视图的画法：正视图(从前向后看)、俯视图(从上往下看)、侧视图(从左往右看，也叫左视图)。

第八讲 点、直线、平面的位置关系。

1、棱柱、圆柱，棱锥、圆锥，棱台、圆台，球的概念与分类及性质。它们的表面积与体积的计算。

棱柱：(1)棱柱的概念：如果一个多面体有两个面互相平行，而其余每相邻两个面的交线互相平行。这样的多面体叫做棱柱。

(2)、棱柱的分类：1)按侧棱是否与底面垂直分类：分为斜棱柱和直棱柱。侧棱不垂直于底面的棱柱叫斜棱柱。侧棱垂直于底面的棱柱叫直棱柱。底面是正多边形的直棱柱叫正棱柱，2)按底面边数的多少分类：底面分别为三角形，四边形，五边形、、、、、、分别称为三棱柱，四棱柱，五棱柱，、、、3)底面是平行四边形的四棱柱叫平行六面体，侧棱与底面垂直的平行六面体叫直平行六面体。底面为矩形的直平行六面体叫长方体，各棱长相等的长方体叫正方体。注正四棱柱一定是长方体，但长方体不一定是正四棱柱，直平行六面体一定是直四棱柱但直四棱柱不一定是直平行六面体。

(3)、棱柱的性质：1)棱柱的各个侧面都是平行四边形，所有的侧棱都相等，直棱柱的各个侧面都是矩形，正棱柱的各个侧面都是全等的矩形。2)与底面平行的截面是与底面对应边互相平行的全等多边形。3)过棱柱不相邻的两条侧棱的截面都是平行四边形。4)棱柱的侧面积=直截面(垂直于侧棱的截面)的周长×侧棱长，棱柱的体积=底面积×高。

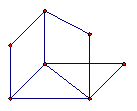
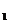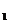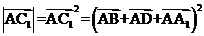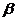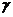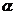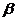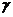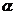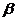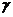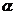(4)、平行六面体ABCD-ABCD的性质：1)平行六面体的对角线交于一点，并且在交点处互相平分，2)平行六面体的四条对角线的平方和等于各棱的平方和。，3)长方体的一条对角线的平方等于一个顶点上三条棱长的平方和。4)若长方体的一条对角线与过这一条对角线的一端的三个相邻面所成的角分别为，，，则Sin+sin+sin=1，5)长方体的体对角线与共顶点的三条棱所成的角分别为，，，则Sin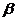+sin+sin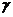=2，6)长方体的对角线等于它的外接球的直径。7)正方体的内切球的直径等于正方形的边长。和正方体各棱切的球的直径等于正方形的面对角线。8){平行六面体}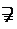{直平行六面体}{长方体}{正四棱柱}{正方体}；

圆柱：一个矩形绕着一边旋转一周所得的几何体。

棱锥：(1)棱锥的概念：如果一个多面体的一个面是多边形，其余各个面是有一个公共顶点的三角形，那么这个多面体叫棱锥。在棱锥中有公共顶点的各三角形叫做棱锥的侧面。过棱锥不相邻的两条侧棱的截面叫棱锥的对角面。

(2)、锥的分类：按照棱锥底面多边形的边数可将棱锥分为：三棱锥、四棱锥、五棱锥…

(3)、棱锥的性质：如果棱锥被平行于底面的平面所截，那么所得的截面与底面相似，截面面积与底面面积的比等于顶点至截面距离与棱锥高的平方比。经过棱锥的高的中点且平行于底面的截面叫中截面，中截面的面积是底面面积的1/4。

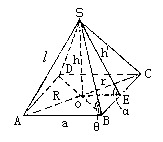
(4)、正棱锥的概念与性质：如果一个棱锥的底面是正多边形，且顶点在底面的射影是底面的中心，这样的棱锥叫正棱锥。性质：1)正棱锥的各侧棱相等，各侧面都是全等的等腰三角形，各等腰三角形底边上的高(叫侧高)也相等。2)正棱锥的高、斜高、斜高在底面的射影、侧棱、底面的外接圆的半径R、底面的半边长可组成四个直角三角形。

(5)、棱锥的体积公式：V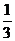＝Sh (S是棱锥的底面积，h是棱锥的高)

提醒：全面积(也称表面积)是各个表面面积之和，故棱柱的全面积＝侧面积+2×底面积；棱锥的全面积＝侧面积+底面积。

圆锥：一个直角三角形绕着一边旋转一周所得的几何体。它的侧面展开图是一个扇形。扇形的弧长是底面圆的周长。扇形的半径等于母线长。

棱台：一个棱锥被平行于底面的平面所截，夹在底面与截面间的几何体叫棱台。

圆台：一个直角梯形绕着垂直于底边的腰旋转一周所得的几何体。

球：(1)、球的概念：与定点的距离等于或小于定长的点的集合叫做球体，简称球。定点叫做球心。定长叫做球的半径。球面：与定点的距离等于定长的点的集合叫做球面。

(2)、球的截面：用一个平面去截球，截面是圆面。球心和截面圆的距离d与球的半径R及截面的半径r之间的关系：r＝　。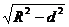

大圆：球面被经过球心的平面截得的圆叫做大圆。小圆：球面被不经过球心的平面截得的圆叫做小圆。经过球面上两点的大圆，当这两点与球心不共线时，有且只有一个。当这两点与球心共线时有无数个。

(3)球面距离：球面上经过两点的大圆在这两点间的一段劣弧的长度，叫做这两点的球面距离。它等于球心角×半径。

(4)球的体积和表面积公式：V＝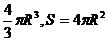

(5)正四面体的边长为a，则它的外接球的半径、内切球的半径、棱切球的半径分别为

，

正方体的边长为a，则它的外接球的半径、内切球的半径、棱切球的半径分别为

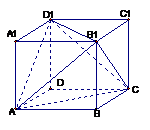
3、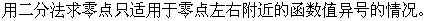

第七讲空间几何体

2、

1、

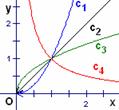
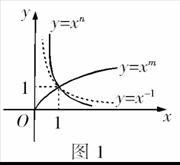
2、幂函数的图象与性质

第六讲函数与方程、零点与二分法