
2、直线的斜率:(1)定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率。直线的斜率常用k表示,即k=tan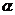 (
(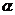 ≠90°).(2)倾斜角为90°的直线没有斜率。(3)经过两点P
≠90°).(2)倾斜角为90°的直线没有斜率。(3)经过两点P (x
(x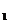 , x
, x ),P
),P (y
(y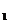 ,y
,y )的直线的斜率公式为
)的直线的斜率公式为
1、直线的倾斜角:(1)定义:在平面直角坐标系中,对于一条与x轴相交的直线l,如果把x轴绕着交点按逆时针方向转到和直线l重合时所转的最小正角记为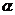 ,那么
,那么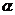 就叫做直线的倾斜角。当直线l与x轴重合或平行时,规定倾斜角为0。(2)直线的倾斜角的范围
就叫做直线的倾斜角。当直线l与x轴重合或平行时,规定倾斜角为0。(2)直线的倾斜角的范围 。(3)在直线的倾斜角的定义中抓住三个重要条件:“逆时针旋转、与直线l重合、最小正角”。
。(3)在直线的倾斜角的定义中抓住三个重要条件:“逆时针旋转、与直线l重合、最小正角”。
12、二面角:平面内的一条直线把平面分为两部分,其中的每一部分都叫做半平面,
从一条直线出发的两个半平面所组成的图形叫二面角,这条直线叫做二面角的棱,
每个半平面叫做二面角的面,棱为l,两个面分别为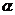 ,
,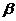 的二面角记为
的二面角记为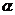 -l-
-l-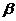 ,
,
一个平面垂直于二面角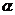 -l-
-l-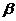 的棱,且与两个半平面的交线分别是射线OA,OB,O为垂足,则∠AOB叫做二面角
的棱,且与两个半平面的交线分别是射线OA,OB,O为垂足,则∠AOB叫做二面角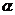 -l-
-l-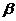 ,的平面角。
,的平面角。
一个二面角的大小可用它的平面角的大小来衡量,二面角的平面角是多少度,就说这个二面角是多少度。二面角大小的取值范围是[0,180°]
计算二面角的方法:(1)定义法(常根据三垂线定理先作平面角即自二面角的一个面上一点向另一个面引垂线,再由垂足向棱作垂线,,再解直角三角形)。(2)射影面积法,(3)有平面角向量法(常用基向量法),(4)法向量法(常用坐标法):
利用法向量可处理二面角问题
设  分别为平面
分别为平面 的法向量,二面角
的法向量,二面角 的大小为
的大小为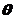 ,向量
,向量
 的夹角为
的夹角为 ,则有
,则有 (图3)或
(图3)或  (图4)
(图4)

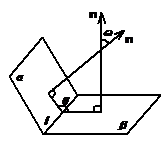
图3 图4
第九讲 直线与方程
11、最小角定理:平面的斜线和它在平面内的射影所成的角是这条斜线和这个平面内任一条直线所成的角中最小的角。设AB是平面a的一条斜线,A为斜足,直线m是平面a内任一直线,AB′是AB在平面a内的射影。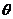 为AB和m所成的角,
为AB和m所成的角, 为AB和射影所成的角,
为AB和射影所成的角, 射影AB′和m所成的角,则cos
射影AB′和m所成的角,则cos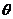 =cos
=cos cos
cos
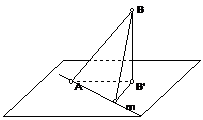 重要应用:空间两条异面直线L1与L2所成的角为
重要应用:空间两条异面直线L1与L2所成的角为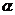 ≠
≠ ,过空间一定点P作直线L与L1,L2所成的角都是
,过空间一定点P作直线L与L1,L2所成的角都是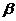 ,这样的直线L可作多少条?
,这样的直线L可作多少条?
分析:(1)若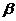 ∈(0,
∈(0,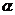 /2),则这样的直线L有0条
/2),则这样的直线L有0条
(2)若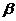 =
=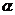 /2,则这样的直线有1条
/2,则这样的直线有1条
(3)若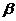 ∈(
∈(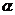 /2,
/2, ),则这样的直线L有2条
),则这样的直线L有2条
(4)若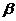 =
= ,则这样的直线L有3条
,则这样的直线L有3条
(5)若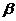 ∈(
∈( ,
, ),则这样的直线L有4条
),则这样的直线L有4条
(6)若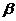 =
= ,则这样的直线L有1条
,则这样的直线L有1条
10、直线和平面所成的角:平面的一条斜线和它在平面内的射影所成的锐角,叫这条直线和这个平面所成的角。特别当一条直线和平面垂直时,就说直线与平面所成的角是直角,当一条直线在平面内或和这个平面平行时,我们规定直线和平面所成的角为0°,所以直线和平面所成的角的范围是
利用法向量可处理线面角问题
设
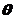 为直线
为直线 与平面
与平面 所成的角,
所成的角, 为直线
为直线 的方向向量
的方向向量 与平面
与平面 的法向量
的法向量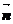 之间的夹角,则有
之间的夹角,则有 (图1)或
(图1)或 (图2)
(图2)

 图1 图2
图1 图2
9、三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。 三垂线定理的逆定理:在平面内的一条直线,如果它和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直。
8、(1)平面与平面的位置关系:1)平行__没有公共点,2)相交__有且只有一条公共直线。两个平面的公共点都在同一条直线上。
(2)两个平面平行的判定:1)一个如果平面内有两条相交直线和另一个平面平行,则这两个平面平行。简称为“线面平行,则面面平行”,2)推论:如果平面内一个有两条相交直线和另一个平面内两条相交直线平行,那么这两个平面平行。3)垂直于同一条直线的两个平面平行。
两个平面平行的性质定理:1)如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
2)两个平行平面之间的距离处处相等,夹在两个平行平面之间的平行线段也相等。
3)如果两个平面平行,那么一个平面内的所有直线都平行于另一个平面。
(3) 两个平面垂直的判定:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
两个平面垂直的性质定理:1)如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。2)如果两个平面垂直,那么从一个平面内一点作另一个平面的垂线必在第一个平面内。
7、(1)直线与平面的位置关系:1)直线在平面内, 2)直线与平面相交, 3)直线与平面平行, 其中直线与平面相交、直线与平面平行都叫作直线在平面外。
(2)直线与平面平行的判定:如果平面内一条直线和这个平面平面平行,那么这条直线和这个平面平行。简称为“线线平行,则线面平行。”
判定直线与平面平行的方法还有:1) 2)
2)
直线与平面平行的性质定理:如果一条直线和一个平面平行,那么经过这条直线的平面和这个平面相交,交线和这条直线平行,简称为“线面平行,则线线平行”。
(3) 直线与平面垂直的概念:如果一条直线和平平面内任何一条直线都垂直,那么这条直线和这个平面垂直。公理:过一点有且只有一条直线和已知平面垂直。
直线和平面垂直的判定:1)一个平面内两条相交直线都垂直,那么这条直线和这个平面垂直。2)两条平行线中有一条直线和一个平面垂直,那么另一条直线也和这个平面垂直。
直线和平面垂直的性质定理:(1)如果一条直线和一个平面垂直,那么这条直线和这个平面内所有直线都垂直。(2)如果两条直线都垂直于同一个平面,那么这两条直线平行。
6、异面直线的距离:(1)和两条异面直线都垂直相交的直线叫异面直线的公垂线。两条异面直线
的公垂线有且只有一条。而和两条异面直线都垂直的直线有无数条。(2)求异面直线的距离的常用方法有:1)直接找公垂线段而求之。2)转化为求直线到平面的距离,即过其中一条直线作平面和平行另一条直线。3)利用向量法:常利用端点在两条异面直线上的有向线段在公垂线的方向向量上的投影。如图: AB为公垂线段,
AB为公垂线段,
异面直线上两点的距离公式:已知两条异面直线a,b所成的角为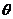 ,在a,b上分别取点E,F,已知AB为公垂线段,长度为d,BE=m,AF=n,EF=l则l=
,在a,b上分别取点E,F,已知AB为公垂线段,长度为d,BE=m,AF=n,EF=l则l= (同侧为减,异侧为加)
(同侧为减,异侧为加)
5、空间直线的位置关系:(1)相交直线:有且只有一个公共点。(2)平行直线:在同一平面内,没有公共点。(3)异面直线:不在任何一个平面内,也没有公共点。两条异面直线的作图,常借助于辅助平面。
异面直线的判定:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线。
异面直线所成的角(或夹角)的定义与求法:直线a,b是异面直线,经过空间一点O,分别引直线aˊ//a , b'//b,相交直线a',b'所成的锐角(直角)叫异面直线a,b所成的角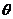 ∈
∈ ,求异面直线的夹角常用平移法和向量法。
,求异面直线的夹角常用平移法和向量法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com