
4、
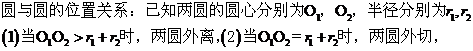
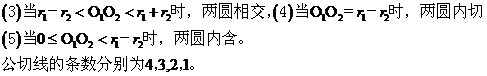
3、
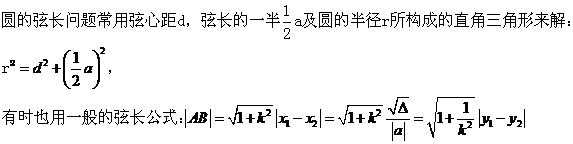
2、
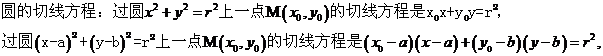
从圆外一点引圆的切线一定有两条,可先设切线方程,再根据相切的条件来求。过两切点的直线方程的求法:先求出以已知圆的圆心和这点为直径端点的圆,该圆与已知圆的公共弦就是过两切点的直线方程。
1、圆的方程的四种形式:(1)圆的标准方程: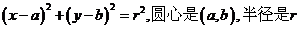 ,特别当圆心是(0,0),半径为r时,
,特别当圆心是(0,0),半径为r时,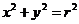 ,(2)圆的一般方程:
,(2)圆的一般方程: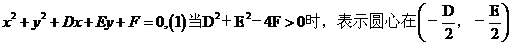
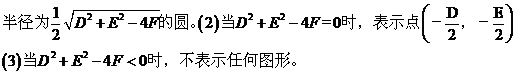
(3)圆的参数方程:圆心在(a,b),半径为r的圆的参数方程是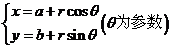
特别当圆心是原点时,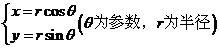
(4)
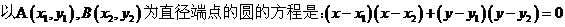
8、直线的极坐标方程。
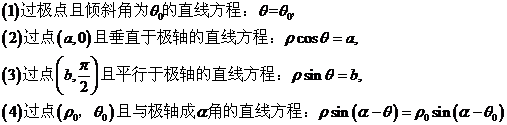
第十讲 圆与方程
7、直线方程的参数形式:
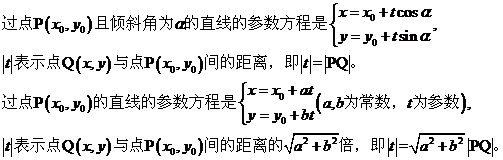
直线的参数方程常用来解决过定点的直线与圆锥曲线相交的问题。
6、到角和夹角公式:(1)l 到l
到l :指直线l
:指直线l 绕着交点按逆时针方向转到和直线l
绕着交点按逆时针方向转到和直线l 重合所转的角
重合所转的角 ,
,
 且tan
且tan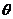 =
=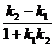 ( k
( k k
k ≠-1).(2)l
≠-1).(2)l 与l
与l 的夹角
的夹角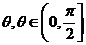 且tan
且tan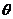 =︱
=︱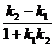 ︱(
k
︱(
k k
k ≠-1)。
≠-1)。
5、直线与直线的位置关系:(1)斜率存在的两直线:l : y=k
: y=k x+b
x+b , l
, l :y=k
:y=k x+b
x+b ,有若l
,有若l ∥l
∥l
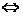 k
k =k
=k ,且b
,且b ≠b
≠b ,若l
,若l ⊥l
⊥l ,
,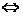 k
k k
k =-1,若l
=-1,若l 与l
与l 相交
相交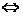 k
k ≠k
≠k ,若l
,若l 与l
与l 重合
重合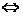 k
k =k
=k ,b
,b =b
=b 。(2)一般的两直线:l
。(2)一般的两直线:l :A
:A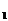 x+B
x+B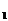 y+C
y+C =0,l
=0,l :A
:A x+B
x+B y+C
y+C =0,有若l
=0,有若l ∥l
∥l
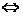 A
A B
B - A
- A B
B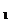 =0,B
=0,B C
C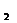 -B
-B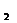 C
C ≠0, (或A
≠0, (或A C
C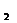 -A
-A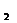 C
C ≠0),若l
≠0),若l ⊥l
⊥l ,
, A
A A
A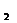 +B
+B B
B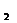 =0,若l
=0,若l 与l
与l 相交
相交 A
A B
B - A
- A B
B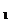 ≠0,若l
≠0,若l 与l
与l 重合
重合 A
A B
B - A
- A B
B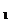 =0,且B
=0,且B C
C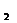 -B
-B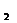 C
C =0,且A
=0,且A C
C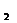 -A
-A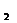 C
C =0
=0
4、点与直线的位置关系:(1)若点P(x ,y
,y )在直线上,则Ax
)在直线上,则Ax +By
+By +C=0.(2) 若点P(x
+C=0.(2) 若点P(x ,y
,y )不在直线上,则Ax
)不在直线上,则Ax +By
+By +C≠0,此时点P(x
+C≠0,此时点P(x ,y
,y )直线的距离d=
)直线的距离d=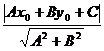 ,
,
(3)由此可得,两平行线l :A
:A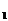 x+B
x+B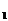 y+C
y+C =0,l
=0,l :A
:A x+B
x+B y+C
y+C =0,间的距离为d=
=0,间的距离为d=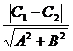
3、直线方程的五种形式:(1)点斜式:已知直线过点(x ,y
,y )斜率为k,则直线方程为:y-y
)斜率为k,则直线方程为:y-y =k(x-x
=k(x-x ),它不包括垂直于x轴的直线。(2)斜截式:已知直线在y轴上的截距为b和斜率k,则直线方程为:y=kx+b,它不包括垂直于x轴的直线。(3)两点式:已知直线经过(x
),它不包括垂直于x轴的直线。(2)斜截式:已知直线在y轴上的截距为b和斜率k,则直线方程为:y=kx+b,它不包括垂直于x轴的直线。(3)两点式:已知直线经过(x ,y
,y ),(x
),(x ,y
,y )两点,则直线方程为:
)两点,则直线方程为:
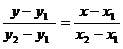 ,它不包括垂直于坐标轴(包括x,y轴)的直线。(4)截距式:已知直线在x轴和y轴上的截距为a,b,则直线方程为:
,它不包括垂直于坐标轴(包括x,y轴)的直线。(4)截距式:已知直线在x轴和y轴上的截距为a,b,则直线方程为: ,它不包括垂直于坐标轴的直线和过原点的直线。
,它不包括垂直于坐标轴的直线和过原点的直线。
(5)一般式:任何直线均可写成:Ax+By+C=0(A,B不同时为0)的形式。
在求直线方程时,要注意斜率是否存在,利用截距式时,不能忽视截距为0的情形,同时要区分“截距”和“距离”。“截距”不是距离,可正可负可为0。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com