

8、向量的长度和两点间的距离公式:
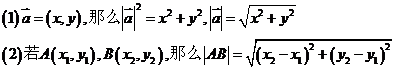
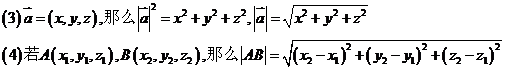
7、、两个向量的夹角:对于非零向量 ,
, ,作
,作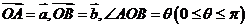 称为向量
称为向量 ,
, 的夹角,当
的夹角,当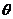 =0时,
=0时, ,
, 同向,当
同向,当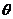 =
=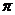 时,
时, ,
, 反向,当
反向,当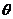 =
=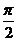 时,
时, ,
, 垂直。
垂直。
向量的数量积:如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为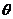 ,我们把数量
,我们把数量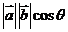 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作:
 ,即
,即
 =
=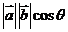 。规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
。规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
向量数量积的性质:设两个非零向量 ,
, 。
。
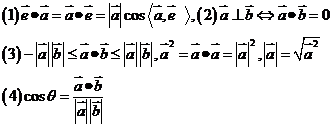
(5)当 ,
, 同向时,
同向时,
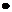
 =
= ,当
,当 与
与 反向时,
反向时,
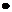
 =-
=-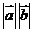 ,当
,当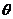 为锐角时,
为锐角时,
 为正且
为正且 ,
, 不同向,
不同向,
 ≠
≠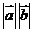 ,当
,当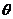 为钝角时,
为钝角时,
 为负且
为负且 ,
, 不反向,
不反向,
 ≠-
≠-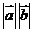 。
。
当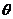 为锐角时,
为锐角时,
 >0,且
>0,且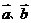 不同向,
不同向,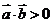 是
是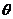 为锐角的必要非充分
为锐角的必要非充分
条件;当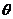 为钝角时,
为钝角时,
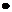
 <0,且
<0,且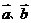 不反向,
不反向,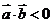 是
是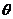 为钝角的必要非充分条件;
为钝角的必要非充分条件;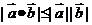 。如(1)已知
。如(1)已知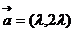 ,
,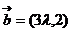 ,如果
,如果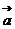 与
与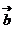 的夹角为锐角,则
的夹角为锐角,则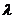 的取值范围是______(答:
的取值范围是______(答: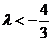 或
或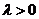 且
且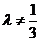 );
);
数量积的的运算律:已知向量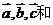 实数
实数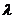 ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。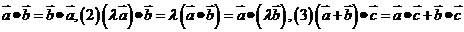
注意下列式子是错误的: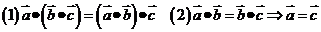
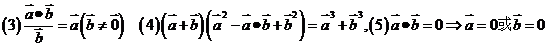 ,
,
平面向量数量积的坐标表示: 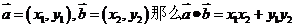 ,
,
空间向量数量积的坐标表示: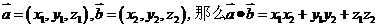
5、向量平行的坐标表示: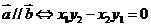 ,对空间向量
,对空间向量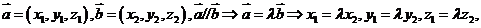
 6、空间直线的向量参数方程 如图:A,B,P三点共线
6、空间直线的向量参数方程 如图:A,B,P三点共线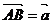
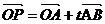 =
=
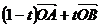 特别当t=
特别当t=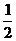 时
时


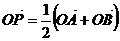 此时P为AB的中点。O为空间任一点。即 P、A、B三点共线
此时P为AB的中点。O为空间任一点。即 P、A、B三点共线
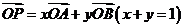
4、平面向量的基本定理:如果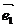 ,
,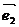 是同一平面内的两个不共线的向量,那么对这一平面内的任一向量
是同一平面内的两个不共线的向量,那么对这一平面内的任一向量 存在唯一的一对有序实数
存在唯一的一对有序实数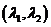 使
使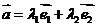 成立,不共线向量
成立,不共线向量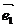 ,
,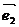 表示这一平面内所有向量的一组基底。
表示这一平面内所有向量的一组基底。
3、向量共线定理: 与非零向量
与非零向量 共线的充要条件是有且只有一个实数
共线的充要条件是有且只有一个实数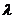 ,使得
,使得 =
=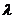
 (
(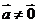 ),
),
2、向量加法:设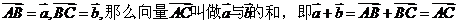
作向量的加法有“三角形法则”和“平行四边形法则”,其中“平行四边形法则”只适用于不共线的向量。
作向量减法有“三角形法则”:设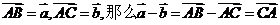 由减向量和终点指向被减向量和终点。注意:此处减向量与被减向量的起点相同。
由减向量和终点指向被减向量和终点。注意:此处减向量与被减向量的起点相同。
1、向量:既有大小又有方向的量,注意向量和数量的区别。向量常用有向线段来表示,有向线段的长度叫向量的模,注意不能说向量就是有向线段。长度为0的向量叫零向量,记作: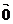 ,注意零向量的方向是任意的。长度为一个单位长度的向量叫做单位向量,常用
,注意零向量的方向是任意的。长度为一个单位长度的向量叫做单位向量,常用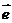 表示。
表示。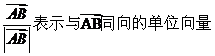 。
。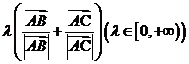 表示∠BAC的角平分线上的向量,共线向量(也叫平行向量):方向相同或相反的非零向量,
表示∠BAC的角平分线上的向量,共线向量(也叫平行向量):方向相同或相反的非零向量, 平行于
平行于 ,记作:
,记作: ∥
∥ ,
,
规定零向量和任何向量平行。注意:相等向量一定是共线向量,但共线向量不一定相等。表示共线向量的有向线段不一定在同一直线上,向量可以平移。
共线向量的方向不一定相同或相反,因为零向量的方程是任意的。
相反向量;长度相等方向相反的向量叫做相反向量。 的相反向量是-
的相反向量是- 。
。
6、关于三角函数的周期:
(1)一般先化为: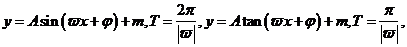
(2)
绝对值或平方对三角函数周期性的影响:一般说来,某一周期函数解析式加绝对值或平方,其周期性是:弦减半、切不变.既为周期函数又是偶函数的函数自变量加绝对值,其周期性不变,其它不定。 如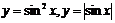 的周期都是
的周期都是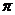 ,
, 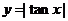 的周期不变;
的周期不变;
第十六讲平面向量与空间向量
5.三角函数的值域的求法:(1)y=asinx+b(或y=acosx+b)型,利用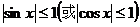 ,即可求解,此时必须注意字母a的符号对最值的影响。
,即可求解,此时必须注意字母a的符号对最值的影响。
(2)y=asinx+bcosx型,引入辅助角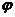 ,化为y=
,化为y=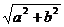 sin(x+
sin(x+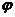 ),利用函数
),利用函数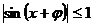 即可求解。Y=asin
即可求解。Y=asin x+bsinxcosx+mcos
x+bsinxcosx+mcos x+n型亦可以化为此类。
x+n型亦可以化为此类。
(3)y=asin x+bsinx+c(或y=acos
x+bsinx+c(或y=acos x+bcosx+c),型,可令t=sinx(t=cosx),-1≤t≤1,化归为闭区间上二次函数的最值问题。
x+bcosx+c),型,可令t=sinx(t=cosx),-1≤t≤1,化归为闭区间上二次函数的最值问题。
(4)Y=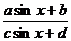 (或y=
(或y=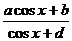 )型,解出sinx(或cosx),利用
)型,解出sinx(或cosx),利用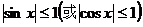 去解;或用分离常数的方法去解决。
去解;或用分离常数的方法去解决。
(5)y=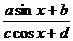 (y=
(y=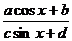 )型,可化归为sin(x+
)型,可化归为sin(x+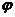 )g(y)去处理;或用万能公式换元后用判别式去处理;当a=c时,还可利用数形结合的方法去处理上。
)g(y)去处理;或用万能公式换元后用判别式去处理;当a=c时,还可利用数形结合的方法去处理上。
(6)对于含有sinx±cosx,sinxcosx的函数的最值问题,常用的方法是令sinx±cosx=t,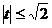 ,将sinxcosx转化为t的函数关系式,从而化为二次函数的最值问题。
,将sinxcosx转化为t的函数关系式,从而化为二次函数的最值问题。
4、反三角函数的定义:(1)反正弦:在闭区间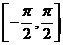 上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中
上符合条件sinx=a(-1≤a≤1)的角x,叫做实数a的反正弦,记作arcsina,即x=arcsina,其中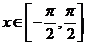 ,且a=sinx.注意arcsina表示一个角,这个角的正弦值为a,且这个角在
,且a=sinx.注意arcsina表示一个角,这个角的正弦值为a,且这个角在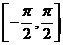 内(-1≤a≤1)
内(-1≤a≤1)
(2)反余弦:在闭区间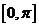 上,符合条件
上,符合条件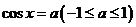 的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x
的角x,叫做实数a的反余弦,记作arccosa,即x=arccosa,其中x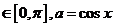 .
.
(3)反正切:在开区间(-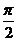 ,
,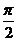 )内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中
)内,符合条件tanx=a(a为实数)的角x,叫做实数a的反正切,记做arctana,即x=arctana,其中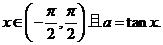
反三角函数的性质:(1)sin(arcsina)=a, (-1≤a≤1),cos(arccosa)=0, (-1≤a≤1),
tan(arctana)=a,(2)arcsin(-a)=-arcsina,arccos(-a)=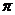 -arccosa,arctan(-a)=-arctana,
-arccosa,arctan(-a)=-arctana,
(3)arcsina+arccosa=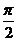 ,(4) arc sin (sinx)=x,只有当x在
,(4) arc sin (sinx)=x,只有当x在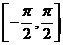 内成立。同理arccos(cosx)=x只有当x在闭区间
内成立。同理arccos(cosx)=x只有当x在闭区间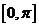 上成立。
上成立。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com