

1、正弦定理:在三角形ABC中,a,b,c分别为角A,B,C的对边,R为三角形ABC的外接圆的半径,则有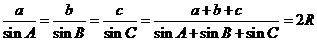 ,注意以下一些变式:
,注意以下一些变式:
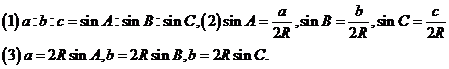
17、平移公式:将点P(x,y),按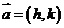 平移至点P′(xˊ,yˊ),
平移至点P′(xˊ,yˊ),
则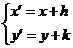 ,
,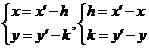 ,
,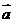 叫平移向量。
叫平移向量。
图象的平移:设函数y=f(x)的图象为C,将C上每一点均按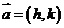 平移,得一个新的图象C′,则C′对应的函数关系式为y-k=f(x-h),即y=f(x-h)+k,
平移,得一个新的图象C′,则C′对应的函数关系式为y-k=f(x-h),即y=f(x-h)+k,
(2)函数 的图象按向量
的图象按向量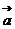 平移后,所得函数的解析式是
平移后,所得函数的解析式是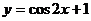 ,则
,则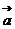 =________(答:
=________(答: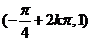 )
)
第十六讲正弦定理与余弦定理
16、在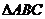 中,①若
中,①若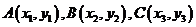 ,则其重心的坐标为
,则其重心的坐标为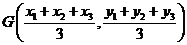 。
。
②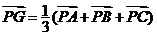
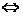
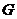 为
为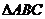 的重心,特别地
的重心,特别地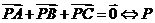 为
为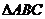 的重心;
的重心;
③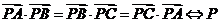 为
为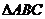 的垂心;
的垂心;
④向量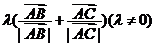 所在直线过
所在直线过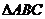 的内心(是
的内心(是 的角平分线所在直线);
的角平分线所在直线);
⑤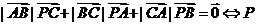
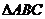 的内心;
的内心;
⑥S⊿AOB=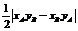
如:(1)若O是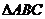 所在平面内一点,且满足
所在平面内一点,且满足 ,则
,则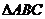 的形状为____(答:直角三角形);(2)若
的形状为____(答:直角三角形);(2)若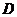 为
为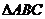 的边
的边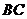 的中点,
的中点,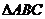 所在平面内有一点
所在平面内有一点 ,满足
,满足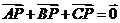 ,设
,设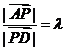 ,则
,则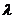 的值为___(答:2);(3)若点
的值为___(答:2);(3)若点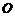 是
是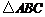 的外心,且
的外心,且 ,则
,则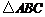 的内角
的内角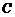 为____(答:
为____(答: );
);
15、线段的定比分点:设点P是直线P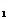 P
P 上异于P
上异于P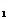 、P
、P 的任意一点,若存在一个实数
的任意一点,若存在一个实数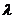 ,使P
,使P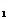 P=
P=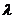 PP
PP ,
,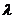 叫做点P分有向线段
叫做点P分有向线段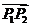 所成的比,P点叫做有向线段
所成的比,P点叫做有向线段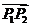 的以定比为
的以定比为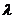 的定比分点。当P点在线段 P
的定比分点。当P点在线段 P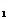 P
P 上时,
上时,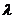 >0,当P点在线段
P
>0,当P点在线段
P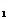 P
P 的延长线上时,
的延长线上时,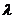 <-1,当P点在线段P
<-1,当P点在线段P P
P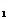 的延长线上时 -1<
的延长线上时 -1<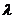 <0。
<0。
若点P分有向线段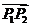 所成的比为
所成的比为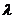 ,则点P分有向线段
,则点P分有向线段 所成的比为
所成的比为
定比分点的坐标公式:
设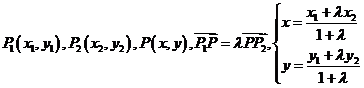
在使用定比分点的坐标公式时,应明确(x,y), (x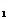 ,y
,y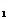 ), (x
), (x ,y
,y )的意义,即分别为分点,起点,终点的坐标。一般在计算中应根据题设,自行确定起点,分点和终点并根据这些点确定对应的定比
)的意义,即分别为分点,起点,终点的坐标。一般在计算中应根据题设,自行确定起点,分点和终点并根据这些点确定对应的定比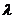 。
。
当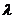 =1时,就得到P
=1时,就得到P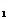 P
P 的中点公式:
的中点公式:
14、向量与平面垂直:如果表示向量 的有向线段所在的直线垂直于平面a,则称这个向量垂直于平面a,此时向量
的有向线段所在的直线垂直于平面a,则称这个向量垂直于平面a,此时向量 叫做平面a的法向量。
叫做平面a的法向量。
13、空间直角坐标系:如果空间的一个基底的三个基向量互相垂直,且长度都为1,则这个基底叫做单位正交基底,常用{i,j,k}表示,而空间坐标系的建立是:在空间选定一点O和一个单位正交基底{i,j,k},以O为原点,分别以i,j,k的方向为正方向建立三条数轴:x轴,y轴,z轴,它们都叫坐标轴,O-xyz为空间坐标系,向量i,j,k为坐标向量,通过每两条数轴的平面叫做坐标平面,分别叫做xOy平面,yOz平面, xOz平面,作空间坐标系时,一般使∠xOy=135°(或45°),∠yOz=90°.在空间坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称此坐标系为右手直角坐标系。
12、空间向量基本定理:如果三个向量 ,
, ,
,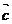 不共面,那么对空间任一向量
不共面,那么对空间任一向量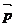 ,存在一个唯一的有序组x,y,z,使
,存在一个唯一的有序组x,y,z,使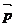 =x
=x +y
+y +z
+z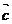 .其中{
.其中{ ,
, ,
,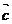 }叫做空间的一个基底,
}叫做空间的一个基底, ,
, ,
,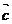 都叫做基向量。
都叫做基向量。
11、向量与平面平行:如果向量所在直线在平面内或与平面平行,则称向量与平面平行。注意与直线与平面平行的区别。
共面向量:平行于同一平面的向量叫做共面向量,空间任意两个向量都共面(包括两条异面直线上的向量)。空间三个向量不一定共面。不共面的三个向量可构成空间的一个基底。
共面向量定理:如果两个向量 ,
, 不共线,则向量
不共线,则向量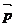 与向量
与向量 ,
, 共面的充要条件是存在实数对x,y,使得
共面的充要条件是存在实数对x,y,使得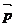 =x
=x +y
+y .
.
共面向量定理的推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y,使 或对空间任一点O,有
或对空间任一点O,有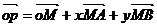
= (m+n+k=1).这也是证四点共面的方法。
(m+n+k=1).这也是证四点共面的方法。
10、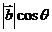 叫
叫 在
在 上的投影。
上的投影。
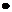
 的几何意义是它等于
的几何意义是它等于 的模
的模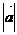 与
与 在
在 上的投影的积。
上的投影的积。
注意:投影也叫射影,是一个数,可正可负也可为0,不再是一个向量。有两种计算方式: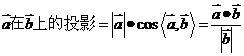
9、 两向量垂直的充要条件:
非零向量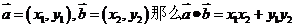 =0
=0
非零向量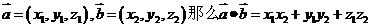 =0
=0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com