
1、椭圆的定义1: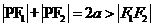 ,F
,F ,F
,F 为两定点即焦点。定义2:
为两定点即焦点。定义2: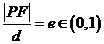
(二)求曲线方程(求轨迹)的几种常用方法:
1、直接法:直接用动点P(x,y)的坐标表示等量关系,化简得轨迹方程。一般步骤是:①建立适当的直角坐标系,用(x,y)表示曲线上任意一点M的坐标;如果题中出现了点的坐标或方程表示已经建立了坐标系。②列出点 M适合条件的几何等量关系;③用坐标表示列出方程f(x,y)=0,④化方程f(x,y)=0为最简形式;⑤证明以化简后的方程的解为坐标的点都是曲线上的点。一般情况下,化简前后的方程的解是相同的,步骤⑤可以省略不写,如有特殊情况,可适当予以说明,另外,根据情况,也可以省略步骤②直接列出直线方程。
例1:三角形ABC的顶点A固定,点A的对边BC的长为2a,边BC上的高线长为b,边BC沿一条定直线移动,求三角形ABC外心的轨迹方程。
分析:以BC边所在的直线为x轴,过A点且与x轴垂直的直线为y轴,建立如图所示的直角坐标系,则B(0,b),设外心M(x,y),则|MA|=|MB|,B(x-a,0),x -2by+b
-2by+b -a
-a =0
=0
2、 定义法:通过圆锥曲线(或已知曲线)定义确定轨迹性质,进而求得方程。
例2、(1)由动点P向圆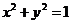 作两条切线PA、PB,切点分别为A、B,∠APB=600,则动点P的轨迹方程为
作两条切线PA、PB,切点分别为A、B,∠APB=600,则动点P的轨迹方程为 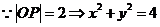
(2)点M与点F(4,0)的距离比它到直线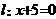 的距离小于1,则点M的轨迹方程是_____
的距离小于1,则点M的轨迹方程是_____
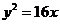
(3) 一动圆与两圆⊙M: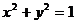 和⊙N:
和⊙N: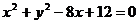 都外切,则动圆圆心的轨迹为 。
都外切,则动圆圆心的轨迹为 。 双曲线的左支上。注:都内切时,得到该双曲线的右支。若与前者内切,与后者外切时,得到双曲线
双曲线的左支上。注:都内切时,得到该双曲线的右支。若与前者内切,与后者外切时,得到双曲线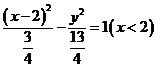 的左支,若与前者外切,与后者内切时,得到双曲线
的左支,若与前者外切,与后者内切时,得到双曲线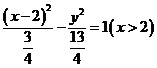 的右支,
的右支,
(4)、
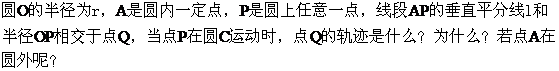
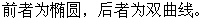
3、相关点代入法:当动点P(x,y)与已知曲线上动点P1(x1,y1)相关时,用x,y表示x1,y1,再代入已知曲线方程,求得轨迹方程。
例3:(1)动点P是抛物线 上任一点,定点为
上任一点,定点为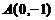 ,点M分
,点M分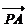 所成的比为2,则M的轨迹方程为__________
所成的比为2,则M的轨迹方程为__________
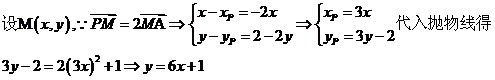
(1) 若点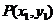 在圆
在圆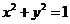 上运动,则点
上运动,则点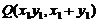 的轨迹方程是____
的轨迹方程是____
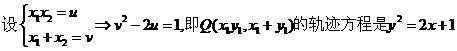
例4、设O为平面直角坐标系的原点,已知定点A(3,0),动点B在曲线x +y
+y =1上运动,∠AOB的平分线交AB于点M,求动点M的轨迹方程。
=1上运动,∠AOB的平分线交AB于点M,求动点M的轨迹方程。
分析:当轨迹上的点的坐标难以直接建立关系时,且已知轨迹上的点的坐标受已知曲线上的某一动点的坐标的影响,可用相关点代入法。本题可用角平分线定理和相关点代入法。
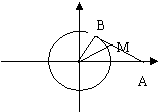 (4x-3)
(4x-3) +16y
+16y =9
=9
4、交轨法:已知所求曲线是某两条曲线的交点可通过解方程组而得。(常与参数法相结合。)
例5、已知直线L1过A(-2,0),直线L2过B(2,0),且L1与L2分别绕A,B旋转,它们在y轴上截距分别为 ,其中
,其中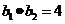 ,试求L1与L2交点的轨迹方程。
,试求L1与L2交点的轨迹方程。
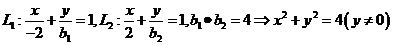
5、参数法。先选定某个变量作为参数,再找出曲线上的点的横坐标、纵坐标与参数的关系式,然后再消去参数。
例6、已知常数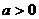 ,在矩形ABCD中,
,在矩形ABCD中,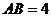 ,
,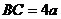 ,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且 ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
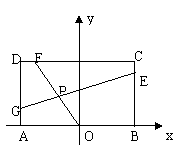
根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在的两定点,使得点P到两点距离的和为定值.按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a)设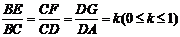
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak)
直线OF的方程为: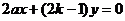 ①
①
直线GE的方程为: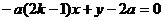 ②
②
从①,②消去参数k,得点P(x,y)坐标满足方程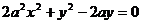
整理得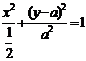 当
当 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当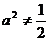 时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长
时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长
当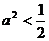 时,点P到椭圆两个焦点(
时,点P到椭圆两个焦点(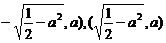 的距离之和为定值
的距离之和为定值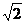

当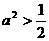 时,点P 到椭圆两个焦点(0,
时,点P 到椭圆两个焦点(0,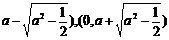 的距离之和为定值2
的距离之和为定值2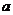 .
.
本题是交轨法与参数法的例子。
例7、(本例是情侣圆锥曲线的求法)
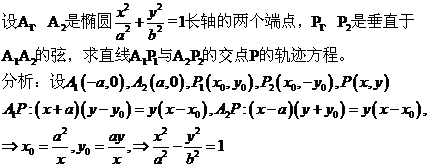
本题是相关点代入法和交轨法相结合。
6、待定系数法:已知曲线方程的类型,可先设出曲线方程的形式,然后求出有关的系数。
例8、
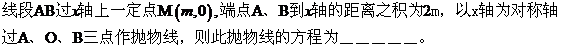

(一)曲线与方程的概念:在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0上的实数解建立了如下的关系:(1)曲线上的点的坐标都是这个方程的解;(2)以这个方程的解为坐标的点都是曲线上的点;那么,这个方程叫曲线的方程;这条曲线叫方程的曲线。
练习:(1)
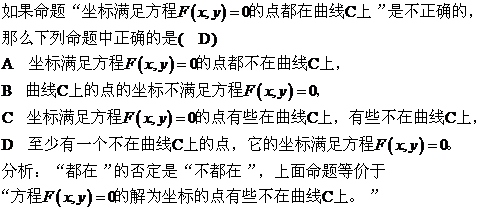
4、全称量词:“所有的”“任意一个”“一切”“每一个”“任给”等。常用“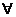 ”表示。含有全称量词的命题叫全称命题。
”表示。含有全称量词的命题叫全称命题。
存在量词:“存在一个”“至少有一个”“有些”“有一个”“有的”
“对某个”等。常用“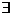 ”表示。含有存在量词的命题叫特称命题。
”表示。含有存在量词的命题叫特称命题。

练习:写出下列命题的否定:(1)p:所有能被3整除的整数都是奇数。
(2)p: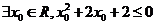
第十九讲圆锥曲线与方程
3、复合命题的三种基本形式及真假判定:P或Q(P∨Q),P且Q(P∧),非P(﹁P)。
“P与﹁P”中的一些常用对应词
|
原结论 |
是(一定是) |
都是(全是) |
>(<) |
至少有一个 |
至多 有一个 |
= |
存在 |
|
反设 |
不是(一定不是) |
不都是 |
≤(≥) |
一个也没有 (都不是) |
至少 有2个 |
≠ |
不存在 |
2、如果已知p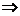 q,则有四种说法:(1)p是q的充分条件,(2)q是p的必要条件,(3)p的一个必要条件是q,(4)q的一个充分条件是P。
q,则有四种说法:(1)p是q的充分条件,(2)q是p的必要条件,(3)p的一个必要条件是q,(4)q的一个充分条件是P。
练习:(1)若ØP是ØQ的必要不充分条件,则P是Q的(A)
A 充分而不必要条件,B 必要不充分条件,C 充要条件,D 既不充分与必要条件
(2)“ 或
或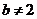 ”是“
”是“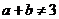 ”成立的
条件(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中的一个).
”成立的
条件(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中的一个). 
1、四种命题:一般地,用p和q分别表示原命题的条件和结论,用﹁p或﹁q分别表示p和q的否定,则四种命题的形式是:(1)原命题:若p则q,(2)逆命题:若q则p,(3)否命题:若﹁p 则﹁q ,(4)逆否命题:若﹁q 则﹁p,
四种命题的真假关系:一个命题与它的逆否命题是等价的,其逆命题与它的否命题也是等价的。要注意区别“否命题”与“命题的否定”:若原命题是“若P则Q”,则这个命题的否定是“若P则非Q”,而它的否命题是“若非P则非Q”。但对于“全称命题”与“特称命题”是互为否定的。
3、线性规划中的几个几何意义:

第十八讲常用的逻辑用语
2、设点P(x ,y
,y ),Q(x
),Q(x ,y
,y ),若Ax
),若Ax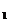 +By
+By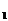 +C与Ax
+C与Ax +By
+By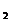 +C同号则P,Q在直线l的同侧,异号则在直线l的异侧。
+C同号则P,Q在直线l的同侧,异号则在直线l的异侧。
(二)恒成立问题:解恒成立问题常用方法:①分离参数法;②数形结合;③转化为函数的最值问题。你能清楚何时用何种方法吗?
常见题型:①若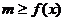 在
在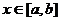 上恒成立,则
上恒成立,则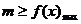 ;若
;若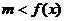 在
在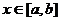 上恒成立,则
上恒成立,则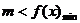 。②若
。②若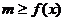 在
在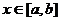 上有解,则
上有解,则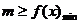 ;若
;若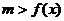 在
在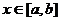 上无解,则
上无解,则 。(注:
。(注: 为常数。)③
为常数。)③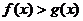 在
在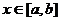 上恒成立,是对于任意的
上恒成立,是对于任意的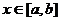 ,
,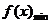 必须大于
必须大于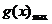 吗?应该怎样解?(不是。通常移项,使
吗?应该怎样解?(不是。通常移项,使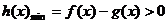 即可;若
即可;若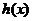 的最值无法求出,则考虑数形结合,只需在
的最值无法求出,则考虑数形结合,只需在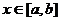 上
上 的图像始终在
的图像始终在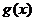 的上方即可。)
的上方即可。)
(1)一次函数型:给定一次函数y=f(x)=ax+b(a≠0),若y=f(x)在[m,n]内恒有f(x)>0,则根据函数的图象(直线)可得上述结论等价于
ⅰ) 或ⅱ)
或ⅱ)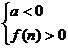 亦可合并定成
亦可合并定成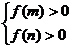
同理,若在[m,n]内恒有f(x)<0,则有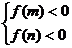
(2)二次函数型:若二次函数y=ax2+bx+c=0(a≠0)大于0恒成立,则有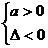
若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解。
例1、 设f(x)=x2-2ax+2,当x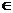 [-1,+
[-1,+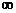 )时,都有f(x)
)时,都有f(x)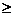 a恒成立,求a的取值范围。
a恒成立,求a的取值范围。
分析:题目中要证明f(x)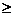 a恒成立,若把a移到等号的左边,则把原题转化成左边二次函数在区间[-1,+
a恒成立,若把a移到等号的左边,则把原题转化成左边二次函数在区间[-1,+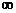 )时恒大于0的问题。
)时恒大于0的问题。
法一:解:设F(x)= f(x)-a=x2-2ax+2-a.
ⅰ)当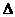 =4(a-1)(a+2)<0时,即-2<a<1时,对一切x
=4(a-1)(a+2)<0时,即-2<a<1时,对一切x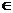 [-1,+
[-1,+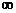 ),F(x)
),F(x) 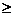 0恒成立;
0恒成立;
ⅱ)当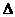 =4(a-1)(a+2)
=4(a-1)(a+2) 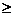 0时由图可得以下充要条件:
0时由图可得以下充要条件:
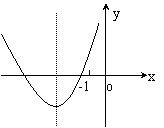
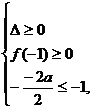 即
即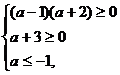
得-3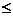 a
a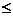 -2;
-2;
综合可得a的取值范围为[-3,1]。
法二:化为求F(x)=
f(x)-a=x2-2ax+2-a.在x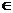 [-1,+
[-1,+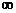 )上的最小值大于等于0。再对对称轴的位置进行讨论。
)上的最小值大于等于0。再对对称轴的位置进行讨论。
法三:分离参数法:再对参数分类讨论:
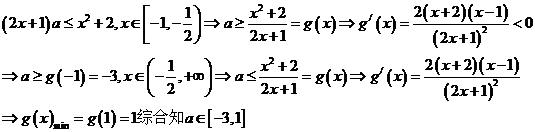
(3)分离变量型:若在等式或不等式中出现两个变量,其中一个变量的范围已知,另一个变量的范围为所求,且容易通过恒等变形将两个变量分别置于等号或不等号的两边,则可将恒成立问题转化成函数的最值问题求解。
例2、 已知当x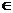 R时,不等式a+cos2x<5-4sinx+
R时,不等式a+cos2x<5-4sinx+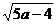 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
分析:在不等式中含有两个变量a及x,其中x的范围已知(x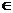 R),另一变量a的范围即为所求,故可考虑将a及x分离。
R),另一变量a的范围即为所求,故可考虑将a及x分离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com