

9、过双曲线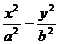 =1外一点P(x
=1外一点P(x ,y
,y )的直线与双曲线只有一个公共点的情况如下:
)的直线与双曲线只有一个公共点的情况如下:
(1) P点在两条渐近线之间且不含双曲线的区域内时,有两条与渐近线平行的直线和分别与双曲线两支相切的两条切线,共四条。(2)P点在两条渐近线之间且包含双曲线的区域内时,有两条与渐近线平行的直线和只与双曲线一支相切的两条切线,共四条。(3)P在两条渐近线上但非原点,只有两条:一条是与另一渐近线平行的直线,一条是切线。(4)P为原点时不存在这样的直线。
此外:P点在双曲线内时,只有两条与渐近线平行的直线。P在双曲线上时有三条:二条是与渐近线平行的直线,一条是切线。
如:过点(0,2)与双曲线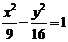 有且仅有一个公共点的直线的斜率的取值范围为______
有且仅有一个公共点的直线的斜率的取值范围为______
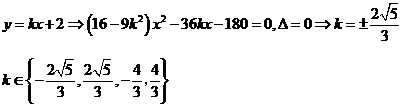
8、过双曲线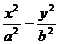 =1上一点P(x
=1上一点P(x ,y
,y )的切线方程是
)的切线方程是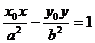 (与椭圆类似,求导数可得斜率。)
(与椭圆类似,求导数可得斜率。)
7、双曲线的第二定义:平面内与一个定点F和一条定直线l的距离的比是常数e(e>1)的动点的轨迹叫双曲线。
6、双曲线: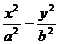 =1按
=1按 =(x
=(x ,y
,y )平移得
)平移得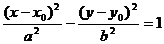 (它的中心、对称轴、焦点、准线方程都按
(它的中心、对称轴、焦点、准线方程都按 =(x
=(x ,y
,y )作了相应的平移。
)作了相应的平移。
5、弦长公式:(1)通径长:
|AB|=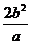 ,是同支上过焦点的所有弦中最短的,注:实轴是异支上过焦点的所有弦中最短的。通径(推广为焦径)为直径的圆和相应的准线对双曲线是相交。(2)过焦点的弦长:|AB|=|e(x
,是同支上过焦点的所有弦中最短的,注:实轴是异支上过焦点的所有弦中最短的。通径(推广为焦径)为直径的圆和相应的准线对双曲线是相交。(2)过焦点的弦长:|AB|=|e(x +x
+x )|,(3)一般的弦长公式:类似于椭圆,x
)|,(3)一般的弦长公式:类似于椭圆,x ,x
,x 分别为弦PQ的横坐标,弦PQ所在直线方程为y=kx+b,代入双曲线方程整理得Ax
分别为弦PQ的横坐标,弦PQ所在直线方程为y=kx+b,代入双曲线方程整理得Ax +Bx+C=0,则
+Bx+C=0,则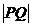 =
=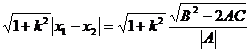 ,若y
,若y ,y
,y 分别为弦PQ的纵坐标,则
分别为弦PQ的纵坐标,则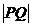 =
=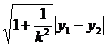 ,
,
4、双曲线的几何性质:对于双曲线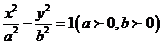
(1)、它的顶点为(-a,0),(a,0),取值范围:x≤-a或x≥a,y∈R,焦点F (-C,0), F
(-C,0), F (C,0),对称轴是坐标轴,对称中心是原点。(2)、准线方程:x=
(C,0),对称轴是坐标轴,对称中心是原点。(2)、准线方程:x=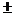
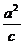
(3)、离心率:e=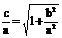 >1,e越大,开口越大,e越小,开口越小。
>1,e越大,开口越大,e越小,开口越小。
(4)、渐近线: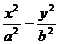 =0(或
=0(或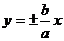 或
或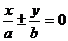 ),已知渐近线方程为
),已知渐近线方程为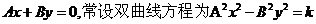 ,
,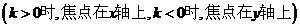
(5)、共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线。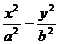 =1与
=1与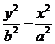 =1互为共轭双曲线,它们有相同的渐近线。
=1互为共轭双曲线,它们有相同的渐近线。
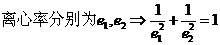 ,
,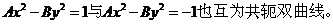 (AB>0),(6)、等轴双曲线:实轴与虚轴相等的双曲线,表示为
(AB>0),(6)、等轴双曲线:实轴与虚轴相等的双曲线,表示为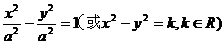 ,P为等轴双曲线上一点,则
,P为等轴双曲线上一点,则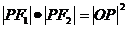 (由焦半径公式和两点间的距离公式可得),等轴双曲线的渐近线为y=
(由焦半径公式和两点间的距离公式可得),等轴双曲线的渐近线为y=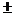 x,离心率e=
x,离心率e=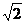
(7)、焦半径公式:|PF |=ex+a, |PF
|=ex+a, |PF |=ex-a(P在右支上,左加右减),若P在左支上则取相应的相反数。即:|PF
|=ex-a(P在右支上,左加右减),若P在左支上则取相应的相反数。即:|PF |=-(ex+a), |PF
|=-(ex+a), |PF |=-(ex-a),焦半径为直径的圆和实轴为直径的圆相切(内切或外切)。
|=-(ex-a),焦半径为直径的圆和实轴为直径的圆相切(内切或外切)。
3、与椭圆类似对于双曲线的焦点三角形有:(1)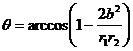 (根据余弦定理可得)(2)
(根据余弦定理可得)(2)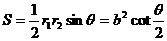 ,(3)双曲线的焦点三角形的内心的横坐标为a或-a.由切线长定理和双曲线的第一定义,联合可得。
,(3)双曲线的焦点三角形的内心的横坐标为a或-a.由切线长定理和双曲线的第一定义,联合可得。
2、双曲线的标准方程:中心在原点,(1)焦点在x轴上: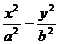 =1(2)焦点在y轴上:
=1(2)焦点在y轴上: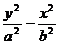 =1(a﹥0,b﹥0)与判断椭圆方程中焦点位置不同的是,双曲线不是通过比较x
=1(a﹥0,b﹥0)与判断椭圆方程中焦点位置不同的是,双曲线不是通过比较x ,y
,y 系数的大小,而是看x
系数的大小,而是看x ,y
,y 的系数的正负号,焦点在系数为正的坐标轴上,简称为“焦点在轴看正号”与椭圆另一个区别在于:的关系是c
的系数的正负号,焦点在系数为正的坐标轴上,简称为“焦点在轴看正号”与椭圆另一个区别在于:的关系是c =a
=a +b
+b (而不是c
(而不是c =a
=a -b
-b )
)
1、双曲线的定义:平面内与两定点F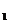 ,F
,F 的距离的差的绝对值等于定长2a(小于|F
的距离的差的绝对值等于定长2a(小于|F F
F |)的点的轨迹叫双曲线,即||PF
|)的点的轨迹叫双曲线,即||PF |-|PF
|-|PF ||=2a(2a<|F
||=2a(2a<|F F
F |。此定义中,“绝对值”与2a<|F
|。此定义中,“绝对值”与2a<|F F
F |,不可忽视。若2a=|F
|,不可忽视。若2a=|F F
F |,则轨迹是以F
|,则轨迹是以F ,F
,F 为端点射线,若2a﹥|F
为端点射线,若2a﹥|F F
F |,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
|,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。
13、椭圆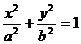 (a﹥b﹥0)按
(a﹥b﹥0)按 =(x
=(x ,y
,y )平移得
)平移得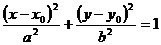 (它的中心、对称轴、焦点、准线方程都按
(它的中心、对称轴、焦点、准线方程都按 =(x
=(x ,y
,y )作了相应的平移。
)作了相应的平移。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com