
8.函数y=ax2+bx+3在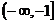 上是增函数,在
上是增函数,在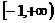 上是减函数,则 ( )
上是减函数,则 ( )
A、b>0且a<0 B、b=2a<0 C、b=2a>0 D、a,b的符号不定
7. 已知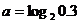 ,
,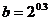 ,
,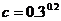 ,则
,则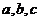 三者的大小关系是 ( )
三者的大小关系是 ( )
A、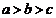 B、
B、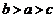 C、
C、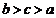 D、
D、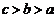
6.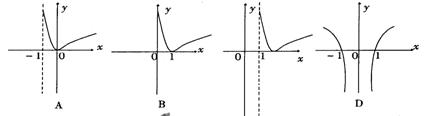 函数y= | lg(x-1)|
的图象是
( )
函数y= | lg(x-1)|
的图象是
( )
5、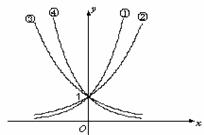 下图是指数函数1
下图是指数函数1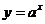 、2
、2 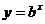 、3
、3 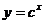 、4
、4 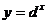 的图象,则
的图象,则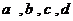 与1的大小关系是( )
与1的大小关系是( )
A.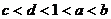 B.
B.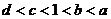
C.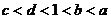 D.
D.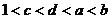
4.设f,g都是由A到A的映射,其对应法则如下表(从上到下):

则与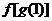 相同的是
(
)
相同的是
(
)
A.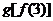 B.
B.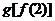 C.
C.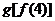 D.
D.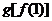
3.函数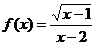 的定义域为
( )
的定义域为
( )
A、[1,2)∪(2,+∞) B、(1,+∞) C、[1,2) D、[1,+∞)
2.设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B= ( )
A、{1,2} B、{1,5} C、{2,5} D、{1,2,5}
1、下列四个集合中,是空集的是( )
A
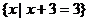 B
B
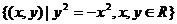
C
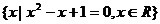 D
D
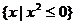
在用放缩法证明不等式时,有时需要“舍掉几个正项”以便达到目的。就是说,如果在和式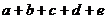 里
里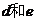 都是正数,可以舍掉
都是正数,可以舍掉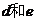 ,从而得到一个明显成立的不等式
,从而得到一个明显成立的不等式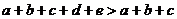 .
.
例如,对于任何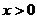 和任何正整数
和任何正整数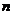 ,由二项式定理可得
,由二项式定理可得
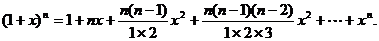
舍掉等式右边第三项及其以后的各项,可以得到不等式: 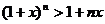 .
.
在后面章节的学习中,我们将会用数学归纳法证明这一不等式的正确性。该不等式不仅当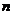 是正整数的时候成立,而且当
是正整数的时候成立,而且当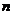 是任何大于1的有理数的时候也成立。这就是著名的贝努利不等式。
是任何大于1的有理数的时候也成立。这就是著名的贝努利不等式。
在今后的学习中,可以利用微积分证明更一般的贝努利不等式:设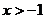 ,则在
,则在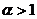 或
或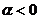 时,
时,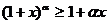 ,在
,在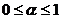 时,
时,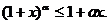
4、其推广形式 ,设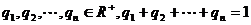 ,
, 是[a,b]上的凸函数,则对任意
是[a,b]上的凸函数,则对任意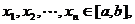 有
有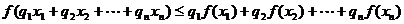 ,
,
当且仅当 时等号成立。
时等号成立。
若 是凹函数,则上述不等式反向。该不等式称为琴生(Jensen)不等式。把琴生不等式应用于一些具体的函数,可以推出许多著名不等式。
是凹函数,则上述不等式反向。该不等式称为琴生(Jensen)不等式。把琴生不等式应用于一些具体的函数,可以推出许多著名不等式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com