
2. 多力平衡:任意一个力与其余各力的合力__________,作用在一条直线上,表示这些力的矢量构成一个首尾相连的闭合多边形.
[考点突破]
考点1.临界问题
(1)临界状态和临界条件
物理学的研究对象在复杂变化中,包含着量变到质变的过程.即当物质(或物体)从一种运动现象(状态或过程)转变为另一种运动现象(状态或过程)时,必然有一个转折点.达到这个转折点,运动的性质就发生变化,否则只能是数量的积累和保持.这个转折点所对应的状态就是临界状态。
①临界状态--是一种物理现象转变为另一种物理现象、或从一个物理过程转变到另一种物理过程的转折状态。常为“恰好出现”、“恰好不出现”的某种状态。
②临界条件--在临界状态时所对应的条件。
包含着临界状态,临界条件判定的物理习题称为临界问题.临界问题是中学物理解题中的一个重要方面.
(2)解决临界问题的方法
解决临界问题的关键:在于找出临界状态,及对应的临界条件。
先找出临界条件,由整体法、隔离法或假设法,根据平衡自相条件,列出方程求解。
(3)常见的几个临界条件是
(1)绳子断与不断的临界问题
绳子“刚好不断裂、刚好断裂”的临界条件是:绳子中张力达最大值Tmax
绳子所能承受的张力是有限度的,绳子断与不断的临界条件是绳中张力等于它所能承受的最大张力。另外还有绳子张紧与松弛的临界条件:绳子张力T=0。
(2)接触与脱离的临界问题
两物体间“恰好不脱离、恰好脱离”的临界条件是:相互作用的挤压力(弹力)N=0
(3)滑动与不滑动的临界问题
两物体间“恰好不滑动、恰好滑动”的临界条件是:静摩擦力达最大值fm
考点2.极值问题
(1)极值:在平衡问题中,某些物理量在变化中可以达到最大值或最小值的现象。
(2)研究极值问题的方法
①解析法:根据平衡条件列出方程,利用数学知识由方程求极值。经常用到的数学知识有二次函数(由根的判别式讨论解的情况)、均分定理、三角函数、几何方法等
②图解法:由平衡条件作出力的矢量图(三力平衡则构成封闭的三角形),再由矢量图进行动态分析,由相关物理量的取值范围,确定最大值和最小值。
比较:图解法简便、直观;解析法有时会较繁琐。
[典题例析]
 类型一、临界条件的应用
类型一、临界条件的应用
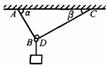
例1. 用AB和CD两根绳悬挂一重物,A、C两点在同一水平面上,AB⊥CD,如图所示。若AC=50cm,AB=30cm,AB绳和CD绳各最多能承受5N和4N的拉力,问最多能悬挂多重的物体?
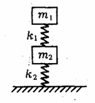
例2.如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接)。整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中下面木块移动的距离为( )

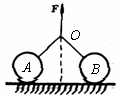 例3. 如图所示,两个完全相同的球A和B,重力大小为G,两球与水平地面间的摩擦因数都为m,一根轻绳两端固结在两个球上,在绳的中点施加一个竖直向上的拉力F,当绳被拉直后,两段绳间的夹角为a.问当F至少为多大时,两球将会发生滑动?
例3. 如图所示,两个完全相同的球A和B,重力大小为G,两球与水平地面间的摩擦因数都为m,一根轻绳两端固结在两个球上,在绳的中点施加一个竖直向上的拉力F,当绳被拉直后,两段绳间的夹角为a.问当F至少为多大时,两球将会发生滑动?
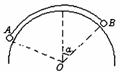 例4.如图所示,质量为
例4.如图所示,质量为 kg的A球和质量为3kg的B球被轻质细线连接后,挂在光滑的柱上恰好处于静止状态,已知∠AOB=90º,求OB与竖直方向的夹角α。
kg的A球和质量为3kg的B球被轻质细线连接后,挂在光滑的柱上恰好处于静止状态,已知∠AOB=90º,求OB与竖直方向的夹角α。
 类型二、极值问题的方法应用
类型二、极值问题的方法应用
例5. 如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60º的拉力F,若要使绳都能伸直,求拉力F的大小范围.
例6. 建筑工地上的黄砂,堆成圆锥形,而不管如何堆放,其角度是不变的。若测出其圆锥底的周长为12.5m,高为1.5m,如图所示。试求:
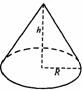 (1)黄砂之间的动摩擦因数。
(1)黄砂之间的动摩擦因数。
(2)若将该黄砂靠墙堆放,占场地的面积至少为多少?
 例7.如图,拉力F作用在重为G的物体上,使它沿水平地面匀速前进.若物体与地面的动摩擦因数为μ,当拉力最小时力和地面的夹角θ为多大?力的最小值为多少?
例7.如图,拉力F作用在重为G的物体上,使它沿水平地面匀速前进.若物体与地面的动摩擦因数为μ,当拉力最小时力和地面的夹角θ为多大?力的最小值为多少?
[问题反思]
第5课时 共点力平衡综合
[知识回顾]
[考点突破]
考点1.整体法和隔离法
(1)整体法:以几个物体构成的系统为研究对象,只分析外力,不需分析内力。
①优缺点:可以避免分析内力,提高解题效率。但不能求出内力。
②整体法选取物体的原则:相互关联的物体;有共同加速度的物体。
(2)隔离法:把系统分解为若干部分从周围的物体中隔离出来研究。
注意:隔离法中所选取的研究对象,可以是单个物体;可以是几个物体组成的整体;也
可以是物体的一部分。
(3)整体法和隔离法的综合运用:
求系统受到的外力作用时,用整体法;
求系统内各物体(或各部分)之间的相互作用时,用隔离法;
在解答一个问题需要多次变换研究对象时,可以将整体法和隔离法交叉使用。
[典题例析]
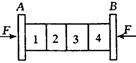 例1.如图所示,两块形状相同的质量忽略不计的竖直木块A、B之间有质量均为m的四块相同的砖,用两个大小均为F的水平力压木板,使砖静止不动,设所有接触面间的动摩擦因数均为μ,则第二块对第三块砖摩擦力的大小为
( )
例1.如图所示,两块形状相同的质量忽略不计的竖直木块A、B之间有质量均为m的四块相同的砖,用两个大小均为F的水平力压木板,使砖静止不动,设所有接触面间的动摩擦因数均为μ,则第二块对第三块砖摩擦力的大小为
( )
A.0 B.mg C.μF D.2mg
 例2.如图所示,球的质量为m,斜面体的质量为M,斜面体的倾角为θ=53°,球光滑,它与墙面、斜面之间没有摩擦力作用.斜面体静止在粗糙的水平面上,这时地面对斜面体的支持力和静摩擦力分别为多大?
例2.如图所示,球的质量为m,斜面体的质量为M,斜面体的倾角为θ=53°,球光滑,它与墙面、斜面之间没有摩擦力作用.斜面体静止在粗糙的水平面上,这时地面对斜面体的支持力和静摩擦力分别为多大?
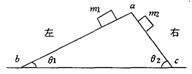 例3. 在粗糙的水平面上有一个三角形木块abc,在它的两个粗糙斜面上分别放两个质量ml和m2的木块,ml>m2 ,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块
( )
例3. 在粗糙的水平面上有一个三角形木块abc,在它的两个粗糙斜面上分别放两个质量ml和m2的木块,ml>m2 ,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块
( )
A.有摩擦力的作用,摩擦力的方向水平向右
B.有摩擦力的作用.摩擦力的方向水平向左
C.有摩擦力的作用、但摩擦力的方向不能确定,因m1、
m2、θ1、θ2的数值并未给出
D.以上结论都不对
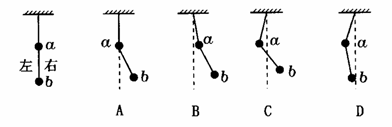
例4.用轻质细线把两个质量未知的小球悬挂起来,如图所示,今对小球a持续施加一个向左偏下300的恒力F,并对小球b持续施加一个向右上偏30º的同样大的恒力F,最后达到平衡,表示平衡状态的图可能是 ( )
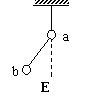
 例5 .一个底面粗糙,质量为 m 的劈放在粗糙水平面上,劈的斜面光滑且与水平面夹角 300,现用一端固定的轻绳系一质量也为 m 的小球,小球与斜面的夹角为
300,如图所示。 ( 1 )当劈静止时绳中拉力为多少? ( 2 )若地面对劈的最大静摩擦力等于地面对劈支持力的μ倍,为使整个系统静止,μ值必须符合什么条件?
例5 .一个底面粗糙,质量为 m 的劈放在粗糙水平面上,劈的斜面光滑且与水平面夹角 300,现用一端固定的轻绳系一质量也为 m 的小球,小球与斜面的夹角为
300,如图所示。 ( 1 )当劈静止时绳中拉力为多少? ( 2 )若地面对劈的最大静摩擦力等于地面对劈支持力的μ倍,为使整个系统静止,μ值必须符合什么条件?
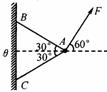
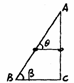 例6.如下图所示,用光滑的粗铁丝做成一个直角三角形,BC边水平,AC边竖直,∠ABC=b。AB及AC两边上分别套有用细线系着的铜环,当它们静止时,细线跟AB所成的角q的大小为( )
例6.如下图所示,用光滑的粗铁丝做成一个直角三角形,BC边水平,AC边竖直,∠ABC=b。AB及AC两边上分别套有用细线系着的铜环,当它们静止时,细线跟AB所成的角q的大小为( )
A.q=b B.q=p/2
C.q <b D.b<q <p /2
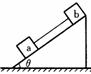
例7.如图所示,用细绳连接两个用同种材料制成的a和b两个物体.它们恰能沿斜面向下作匀速运动,且绳子刚好伸直,关于a、b的受力情况( )
A.a受3个力,b受4个力 B.a受4个力,b受3个力
C.a、b均受3个力 D.a、b均受4个力
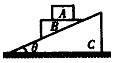
例8.如图所示,倾角为θ的斜面C固定在水平面上.木块A、B的质量分别为m、M,始终保持相对静止,共同沿斜面下滑.B的上表面水平,B、C间的动摩擦因数为μ.(1)当A、B共同匀速下滑;(2)当A、B共同加速下滑时,分别求A、B所受的各力.
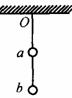 例9.如图所示,将两个质量均为m的小球,用细线相连悬挂于O点.求:
例9.如图所示,将两个质量均为m的小球,用细线相连悬挂于O点.求:
(1)若用力F拉小球a,使其悬线Oa向右偏离竖直方向θ=30º角,且整个装置处于平衡状态.求力F的最小值并说明其方向.
(2)若在a球上施加符合(1)题条件的力F后,仍保持悬线Oa竖直,且使整个装置处于平衡状态.求在b小球上施加的最小力的大小,并说明其方向.
[问题反思]
第6课时 实验:探究弹力和弹簧伸长的关系
实验:验证力的平行四边形定则
[知识回顾]
例9 重G的均匀绳两端悬于水平天花板上的A、B两点。静止时绳两端的切线方向与天花板成α角。求绳的A端所受拉力F1和绳中点C处的张力F2。
[问题反思]
第4课时 共点力平衡专题
[知识回顾]
1. 三力平衡:物体受到三个力作用处于平衡状态时,任意两个力的合力与第三个力__________,作用在_____________上;表示三个力的矢量构成一个首尾相连的闭合的三角形.
例8 (2003年江苏)当物体从高空下落时,空气阻力随速度的增大而增大,因此经过一段距离后将匀速下落,这个速度称为此物体下落的稳态速度。已知球形物体速度不大时所受的空气阻力正比于速度v,且正比于球半径r,即阻力f=krv,k是比例系数。对于常温下的空气,比例系数k=3.4×10-4Ns/m2。已知水的密度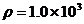 kg/m3,重力加速度为
kg/m3,重力加速度为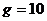 m/s2。求半径r=0.10mm的球形雨滴在无风情况下的稳态速度。(结果保留两位有效数字)
m/s2。求半径r=0.10mm的球形雨滴在无风情况下的稳态速度。(结果保留两位有效数字)
 例6 有一个直角支架AOB,AO水平放置,表面粗糙, OB竖直向下,表面光滑。AO上套有小环P,OB上套有小环Q,两环质量均为m,两环由一根质量可忽略、不可伸长的细绳相连,并在某一位置平衡(如图所示)。现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力FN和摩擦力f的变化情况是
例6 有一个直角支架AOB,AO水平放置,表面粗糙, OB竖直向下,表面光滑。AO上套有小环P,OB上套有小环Q,两环质量均为m,两环由一根质量可忽略、不可伸长的细绳相连,并在某一位置平衡(如图所示)。现将P环向左移一小段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力FN和摩擦力f的变化情况是
A.FN不变,f变大 B.FN不变,f变小 C.FN变大,f变大 D.FN变大,f变小
例7 如图所示,甲、乙两个带电小球的质量均为m,所带电量分别为q和-q,两球间用绝缘细线连接,甲球又用绝缘细线悬挂在天花板上,在两球所在的空间有方向向左的匀强电场,电场强度为E,平衡时细线都被拉紧.
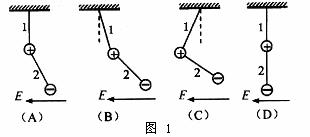
(1)平衡时可能位置是图中的( )
(2)1、2两根绝缘细线的拉力大小分别为( )
A.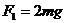 ,
,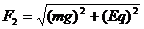 B.
B.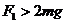 ,
,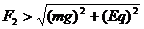
C.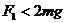 ,
,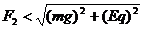 D.
D.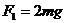 ,
,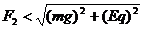
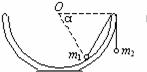 例1 (2003年理综)如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°。两小球的质量比
例1 (2003年理综)如图所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°。两小球的质量比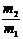 为( )
为( )
A. B.
B. C.
C. D.
D.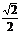
 类型二.动态平衡类问题的分析方法
类型二.动态平衡类问题的分析方法
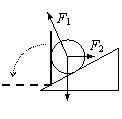
例2 重G的光滑小球静止在固定斜面和竖直挡板之间。若挡板逆时针缓慢转到水平位置,在该过程中,斜面和挡板对小球的弹力的大小F1、F2各如何变化?
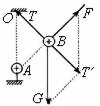 例3 如图所示整个装置静止时,绳与竖直方向的夹角为30º。AB连线与OB垂直。若使带电小球A的电量加倍,带电小球B重新稳定时绳的拉力多大?
例3 如图所示整个装置静止时,绳与竖直方向的夹角为30º。AB连线与OB垂直。若使带电小球A的电量加倍,带电小球B重新稳定时绳的拉力多大?
 类型三.平衡问题中的极值分析
类型三.平衡问题中的极值分析
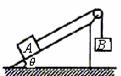
例4 跨过定滑轮的轻绳两端,分别系着物体A和物体B,物体A放在倾角为θ的斜面上(如图所示),已知物体A的质量为m ,物体A与斜面的动摩擦因数为μ(μ<tanθ),滑轮的摩擦不计,要使物体A静止在斜面上,求物体B的质量的取值范围。
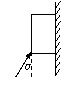 例5 用与竖直方向成α=30°斜向右上方,大小为F的推力把一个重量为G的木块压在粗糙竖直墙上保持静止。求墙对木块的正压力大小N和墙对木块的摩擦力大小f。
例5 用与竖直方向成α=30°斜向右上方,大小为F的推力把一个重量为G的木块压在粗糙竖直墙上保持静止。求墙对木块的正压力大小N和墙对木块的摩擦力大小f。
740.当钠等碱金属单质着火时,可用于灭火的是
A.干冰 B.水
C.细砂 D.煤油
739.在下列直接转化过程中,钠元素发生还原反应的是
A.Na Na2O2 B.Na
Na2O2 B.Na NaOH
NaOH
C.NaCl Na D.NaOH
Na D.NaOH Na2SO4
Na2SO4
738.保存少量金属钠的方法是( )
A.浸入冷水中 B.浸入饱和食盐水中
C.浸入酒精中 D.浸入煤油中
737.下列各种元素,在自然界中无游离态的是( )
A.氧 B.氮
C.钠 D.碳
736.将70 g Na2O2和Na2O的混合物跟98 g 水充分反应后,所得氢氧化钠溶液的质量分数为50%.试通过计算回答原混合物中过氧化钠和氧化钠的质量各多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com