2．学会灵活运用图象处理物理问题的方法。

1．学会用控制变量法研究物理规律。

2．求解临界问题的关键：抓住满足临界值的条件，准确地分析物理过程，进行求解。

[典题例析]

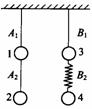例1．四个质量均为m的小球，分别用三条轻绳和一根轻弹簧连接，处于平衡状态，如图所示，现突然迅速剪断轻绳A₁、B₁，让小球下落，在剪断轻绳的瞬间，设小球1、2、3、4的加速度分别用a₁、a₂、a₃和a₄表示，则　　　　　　( 　A　)

A．a₁＝g、a₂＝g、a₃＝2g、a₄＝0

B．a₁＝0、a₂＝2g、a₃＝0、a₄＝g

C．a₁＝g、a₂＝g、a₃＝g、a₄＝g

D．a₁＝0、a₂＝2g、a₃＝g、a₄＝g

『巩固』如图(a)、(b)所示，图中细线均不可伸长，物体均处于平衡状态。如果突然把两水平细线剪断，求剪断瞬间小球A、B加速度怎样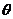？(角已知)

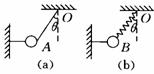
(a)gsinθ、(b)gtanθ

例2．在光滑的水平面上有一质量为m＝1kg的小球，小球与水平轻弹簧和与水平方向成θ＝30°角的轻绳的一端相连，如图所示，此时小球处于静止状态，且水平面对小球的弹力恰好为零．当剪断轻绳的瞬间，小球的加速度大小及方向如何?此时轻弹簧的弹力与水平面对球的弹力的比值是多少? ()

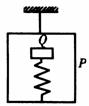例3．如图所示，吊篮P悬挂在天花板上，与吊篮质量相等的物体Q被固定在吊篮中的轻弹簧托住．当悬挂吊篮的细绳烧断的瞬间，吊篮P和物体Q的加速度大小分别是多少？

(0；2g)

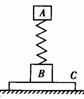『巩固』如图所示，木块A与B用一轻质弹簧相连，竖直放在木板C上，三者静置于水平面上，A与B质量之比是1∶2，B与C、C与水平面间摩擦均不计，在沿水平方向将C迅速抽出的瞬间，A和B的加速度分别是　　(　D　)

A．g、g　　B．0、g　　C．0、3g　　D．0、3g／2

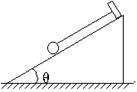例4．如图，一个质量为0.2kg的小球用细绳吊在倾角θ＝37°的斜面顶端，斜面静止时球紧靠在斜面上，绳与斜面平行，不计磨擦，当斜面以10m／s²的加速度向右运时，求绳子的拉力及斜面对小球的弹力． (2.8；0.4)

例5．一条不可伸长的轻绳跨过质量可忽赂不计的定滑轮，绳的一端系一质量M＝15kg的重物，重物静止于地面上，有一质量m＝10kg的猴子，从绳的另一端沿绳向上爬，如图所示，不计滑轮摩擦．在重物不离开地面的条件下，猴子向上爬的最大加速度为　(　B　)(g＝10m／s²)

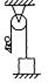A．25m／s²　　　　 B．5m／s²　　 C．10m／s²　　 D．15m／s²

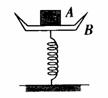例6．如图所示，物体A静止在台秤上，质量m_A＝10.5kg，秤盘B质量m_B＝1.5kg，弹簧本身质量不计，劲度系数k＝800N／m，台秤放在水平桌面上，现给A加一个竖直向上的力，使A向上做匀加速运动，已知力F在0.2s内为变力，0.2s后为恒力。求F的最小值和最大值。(g＝10m／s²)　 (答案：72N，168N)

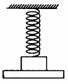
『巩固』一根劲度系数为k，质量不计的轻弹簧，上端固定，下端系一质量为m的物体．有一水平木板将物体托住，并使弹簧处于自然长度，如图所示．现让木板由静止开始以加速度a匀加速向下移动，且a＜g．经过多长时间木板开始与物体分离？

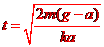
[问题反思]

第7课时 实验： 探究加速度与力、质量的关系

[知识回顾]

[考点突破]一．实验目的：

1．临界状态：在物体的运动状态变化过程中，往往达到某个特定状态时，有关的物理量将发生突变，此状态叫临界状态。相应的待求物理量的值叫临界值。

109.65；0.61，方向水平向左)

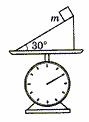
『巩固』如图所示，在托盘测力计的托盘内固定一个倾角为30°的光滑斜面，现将一个重4N的物体放在斜面上，让它自由滑下，那么测力计因4N物体的存在，而增加的读数为多少？

(1)

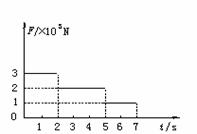例6．质量为200 kg的物体，置于升降机内的台秤上，从静止开始上升.运动过程中台秤的示数F与时间t的关系如图所示，求升降机在7s钟内上升的高度(取g＝10 m／s²)。

(50)

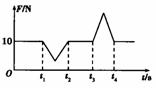
『巩固』某实验小组，利用DIS系统观察超重和失重现象．他们在学校电梯房内做实验，在电梯天花板上固定一个力传感器，测量挂钩向下，并在钩上悬挂一个重为10N的钩码，在电梯运动过程中，计算机显示屏上显示出如图所示图象，以下根据图象分析所得结论错误的是(　D　 )

A．该图象显示出了力传感器对钩码的拉力大小随时间的变化情况

B．从时刻t₁到t₂，钩码处于失重状态，从时刻t₃到t₄，钩码处于超重状态

C．电梯可能开始在15楼，先加速向下，接着匀速向下，再减速向下，最后停在1楼

D．电梯可能开始在l楼，先加速向上，接着匀速向上，再减速向上，最后停在15楼

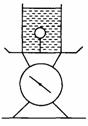例8．如图所示，台秤上有一装水容器，容器底部用一质量不计的细线系住一个空心小球，体积为1.2×10^－3m3，质量为1kg．这时台秤的读数为40N；剪断细线后，在小球上升的过程中，台秤的读数是多少？(ρ_水＝1.0×10³ kg／m³)(39.6)

[问题反思]

第6课时牛顿运动定律的应用(四)

(瞬态问题与临界问题)

[知识回顾]

[考点突破]

考点1．分析瞬时问题的方法技巧：

分析物体的瞬时问题，关健是分析瞬时前后的受力情况及运动状态，再由牛顿第二定律求出瞬时加速度，此类问题应注意两种基本模型的建立。

⑴钢性绳(或接触面)：认为是一种不发生明显形变就能产生弹力的物体，若剪断(或脱离)后、其中弱力立即消失，不需要形变恢复时间，一般题目中所给细一和接触面在不加特珠说明时，均可按此模型处理．

⑵弹簧(或橡皮绳)：此种物体的特点是形变量大，形变恢复需要较长时间，在瞬时问题中，其弹力的大小往往可以看成不变。

考点2．临界问题：

3．当 视重＞重力 时，物体处于超重状态，此时重力并没有增加；

　 当 视重＜重力 时，物体处于失重状态，此时重力并没有减小。

当 视重＝0时，物体处于完全失重状态，平常一切由重力产生的物理现象都会完全消失，如单摆停摆、天平失效等。

[典题例析]

例1．游乐园中，乘客乘坐能加速或减速运动的升降机，可以体会超重或失重的感觉，下列描述正确的是　　　　　　　　　　　　　　　　　　　　 ( 　BC　 )

A．当升降机加速上升时，游客是处在失重状态

B．当升降机减速下降时，游客是处在超重状态

C．当升降机减速上升时，游客是处在失重状态

D．当升降机加速下降时，游客是处在超重状态

例2．质量是60Kg的人站在升降机中的体重计上，当升降机做下列各种运动时，体重计的读数是多少？(g＝10m／s²)

⑴升降机匀速上升。

⑵升降机以4m／s²的加速度加速上升。

⑶升降机以5m／s²的加速度加速下降。(600；840；300)

例3．在一种能获得强烈超重、失重的巨型娱乐设施中，用电梯把乘有十多人的座舱，关在大约二十几层楼的高处，然后让座舱自由下落，落到一定位置时，制动系统开始启动，座舱匀减速运动到地面时恰好停下．已知座舱开始下落时高度为75 m，当落到离地30m时开始制动，若某人托着5 kg的铅球做此游戏，问：

⑴当座舱落到离地高度40m左右的位置时，托着铅球的手感觉如何？

⑵当座舱落到离地高度15 m左右的位置时，手用多大力才能托住铅球？(g＝10m／s²)

(无压力，完全失重；125N)

例4．某人在以2.5m／s²的加速度匀加速下降的升降机里，最多能举起80kg的物体，他在地面上最多能举起　　　 kg的物体；若此人在一匀加速上升的升降机中最多能举起40kg的物体，则此升降机上升的加速度为　　m／s² ？(g＝10m／s²)(60；5)

例5．如图所示，三个质量相同、形状相同的斜面体放在水平地面上，另有三个质量相同的小物体分别从斜面顶端沿斜面滑下。由于小物体跟斜面间的摩擦力不同，第一个小物体匀加速下滑；第二个小物体匀速下滑；第三个小物体以初速度v₀匀减速下滑。三个斜面体都不动，则在小物体下滑的过程中，斜面体对地面压力大小的关系是　　 (　 B　 )

A．N₁＝N₂＝N₃　　　　　　　　　　 B．N₁＜N₂＜N₃

C．N₁＞N₂＞N₃　　　　　　　　　 　D．N₁＜N₂ ＝N₃

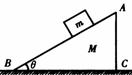『巩固』一质量M＝10kg的木楔ABC静止在粗糙水平地面上，木楔与水平地面间的动摩擦因数μ＝0.02．在木楔的倾角θ为30°的斜面上，有一质量m＝1.0kg的物块由静止开始沿斜面下滑，当滑行路程x＝1.4m时，其速度v＝1.4m/s．在这过程中，木楔没有动．求地面对木楔的支持力及摩擦力的大小和方向(重力加速度取g＝10m/s²)．

2．视重：物体对水平支持面的压力(或对悬挂物的拉力)叫做物体的视重．与物体的运动状态有关。

1．重力：G=mg，重力只与质量成正比，当质量确定，物体所受的重力就确定，与物体的运动状态无关。

3．完全失重：当竖直向下的加速度正好等于g时，称物体处于完全失重状态。此时物体对水平支持面的压力(或对悬挂物的拉力)等于零。

即　　mg－F_N＝ma　得　　F_N＝0

考点2．视重和重力的区别：

2．失重：当物体具有向下的加速度时(向下加速运动或向上减速运动)，称物体处于失重状态．此时物体对水平支持面的压力(或对悬挂物的拉力)小于物体的重力．

即　　mg－F_N＝ma　得　　F_N＝mg－ma＜G