
1、用描述法表示下列集合
①{1,4,7,10,13}
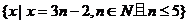
②{-2,-4,-6,-8,-10}
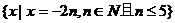
(三) 有限集与无限集
1、 有限集:含有有限个元素的集合
2、 无限集:含有无限个元素的集合
3、 空集:不含任何元素的集合 记作Φ,如:
记作Φ,如: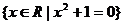
1、列举法:把集合中的元素一一列举出来,写在大括号内表示集合
例如,由方程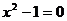 的所有解组成的集合,可以表示为{-1,1}
的所有解组成的集合,可以表示为{-1,1}
注:(1)有些集合亦可如下表示:
从51到100的所有整数组成的集合:{51,52,53,…,100}
所有正奇数组成的集合:{1,3,5,7,…}
(2)a与{a}不同:a表示一个元素,{a}表示一个集合,该集合只
有一个元素
2、描述法:用确定的条件表示某些对象是否属于这个集合,并把这个条
件写在大括号内表示集合的方法
格式:{x∈A| P(x)}
含义:在集合A中满足条件P(x)的x的集合
例如,不等式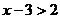 的解集可以表示为:
的解集可以表示为: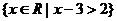 或
或
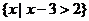

所有直角三角形的集合可以表示为:
注:(1)在不致混淆的情况下,可以省去竖线及左边部分
如:{直角三角形};{大于104的实数}
(2)错误表示法:{实数集};{全体实数}
3、文氏图:用一条封闭的曲线的内部来表示一个集合的方法
4、何时用列举法?何时用描述法?
⑴有些集合的公共属性不明显,难以概括,不便用描述法表示,只能用列举法 如:集合
如:集合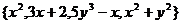
⑵有些集合的元素不能无遗漏地一一列举出来,或者不便于、不需要一一列举出来,常用描述法
如:集合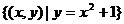 ;集合{1000以内的质数}
;集合{1000以内的质数}
例 集合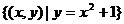 与集合
与集合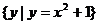 是同一个集合吗?
是同一个集合吗?
答:不是 因为集合
因为集合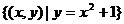 是抛物线
是抛物线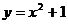 上所有的点构成的集合,集合
上所有的点构成的集合,集合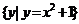 =
=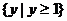 是函数
是函数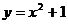 的所有函数值构成的数集
的所有函数值构成的数集
5、(1)集合通常用大写的拉丁字母表示,如A、B、C、P、Q……
元素通常用小写的拉丁字母表示,如a、b、c、p、q……
(2)“∈”的开口方向,不能把a∈A颠倒过来写
4、集合中元素的特性
(1)确定性:按照明确的判断标准给定一个元素或者在这个集合里,
或者不在,不能模棱两可
(2)互异性:集合中的元素没有重复
(3)无序性:集合中的元素没有一定的顺序(通常用正常的顺序写出)
3、元素对于集合的隶属关系
(1)属于:如果a是集合A的元素,就说a属于A,记作a∈A
(2)不属于:如果a不是集合A的元素,就说a不属于A,记作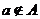
2、常用数集及记法
(1)自然数集:全体非负整数的集合 记作N,
记作N,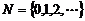
(2)正整数集:非负整数集内排除0的集 记作N*或N+ ,
记作N*或N+ ,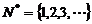
(3)整数集:全体整数的集合 记作Z ,
记作Z , 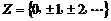
(4)有理数集:全体有理数的集合 记作Q ,
记作Q , 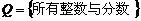
(5)实数集:全体实数的集合 记作R,
记作R,
1、集合的概念
(1)集合:某些指定的对象集在一起就形成一个集合
(2)元素:集合中每个对象叫做这个集合的元素
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com