
例1 计算① cos105°
②cos15° ③cos cos
cos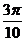 -sin
-sin sin
sin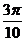
解:①cos105°=cos(60°+45°)=cos60°cos45°-sin60°sin45°
=
②cos15° =cos(60°-45°)=cos60°cos45°+sin60°sin45°
=
③cos cos
cos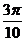 -sin
-sin sin
sin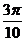 = cos(
= cos( +
+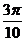 )=cos
)=cos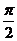 =0
=0
例2已知sina=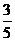 ,cosb=
,cosb=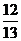 求cos(a-b)的值
求cos(a-b)的值
解:∵sina=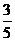 >0,cosb=
>0,cosb=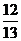 >0
>0
∴a可能在一、二象限,b在一、四象限
若a、b均在第一象限,
则cosa=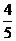 ,sinb=
,sinb= cos(a-b)=
cos(a-b)=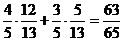
若a在第一象限,b在四象限,
则cosa=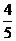 ,sinb=-
,sinb=- cos(a-b)=
cos(a-b)=
若a在第二象限,b在一象限,
则cosa=-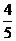 ,sinb=
,sinb= cos(a-b)=
cos(a-b)=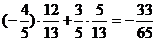
若a在第二象限,b在四象限,
则cosa=-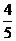 ,sinb=-
,sinb=- cos(a-b)=
cos(a-b)=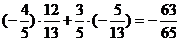
例3已知cos(2α-β)=-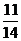 ,sin (α-2β)=
,sin (α-2β)= ,且
,且 <α<
<α< ,0<β<
,0<β< ,
,
求cos(α+β)的值
分析:已知条件中的角与所求角虽然不同,但它们之间有内在联系,
即(2α-β)-(α-2β)=α+β 由α、β角的取值范围,分别求出2α-β、α-2β角的正弦和余弦值,再利用公式即可求解
由α、β角的取值范围,分别求出2α-β、α-2β角的正弦和余弦值,再利用公式即可求解
解:∵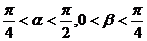 ,
,
∴ <2α-β<π,-
<2α-β<π,-  <α-2β<
<α-2β< ,
,
由cos(2α-β)=-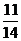 得,sin (2α-β)=
得,sin (2α-β)= ;
;
由sin (α-2β)= 得,cos(α-2β)=
得,cos(α-2β)=

∴cos(α+β)=cos[(2α-β)-(α-2β)]=cos(2α-β)cos(α-2β)+sin (2α-β)sin (α-2β)=- 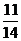 ×
× +
+ ×
× =
=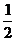

评注:在三角变换中,首先应考虑角的变换 如何变换角?一定要根据题目的条件与结论来变,简单地说就是“据果变形”,创造出使用三角公式的条件,以达到求值、化简和证明的目的
如何变换角?一定要根据题目的条件与结论来变,简单地说就是“据果变形”,创造出使用三角公式的条件,以达到求值、化简和证明的目的 常用的变换角的方法有:α=(α+β)-β,α+2β=(α+β)+α,α=
常用的变换角的方法有:α=(α+β)-β,α+2β=(α+β)+α,α=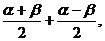
 ,…
,…
8.探究 cos(a-b)的公式
以-b代b得: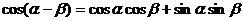
公式记号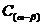
7.探究 特征
①熟悉公式的结构和特点;
②此公式对任意a、b都适用
③公式记号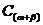
6.探究 由 =
= 导出公式
导出公式
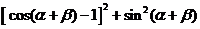
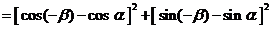
展开并整理得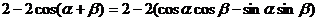
所以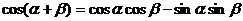 可记为
可记为 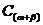
5.计算 ,
,
 =
=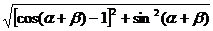
 =
=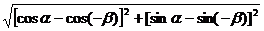
4.探究:写出4个点的坐标
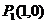 ,
,
 ,
,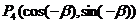 ,
,
3.探究:作单位圆,构造全等三角形
2.探究:在坐标系中a、b角构造a+b角
1.探究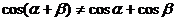
反例:
问题: 的关系?
的关系?
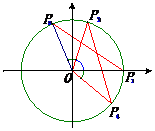 解决思路:探讨三角函数问题的最基本的工具是直角坐标系中的单位圆及单位圆中的三角函数线
解决思路:探讨三角函数问题的最基本的工具是直角坐标系中的单位圆及单位圆中的三角函数线
3.练习:已知A(-1,5),B(4,-7) 求AB
解: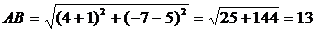
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com