
22.(14分)设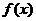 是定义在[-1,1]上的奇函数,且对任意
是定义在[-1,1]上的奇函数,且对任意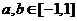 ,当
,当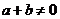 时,都有
时,都有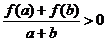 .
.
(1) 若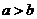 ,试比较
,试比较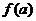 与
与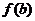 的大小;
的大小;
(2) 解不等式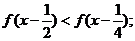
(3)
如果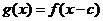 和
和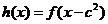 这两个函数的定义域的交集为空集,求
这两个函数的定义域的交集为空集,求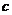 的取值范围.
的取值范围.
21.(12分)在数列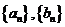 中,
中, 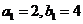 ,且
,且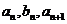 成等差数列,
成等差数列, 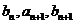 成等比数列
成等比数列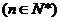 .
.
(1)求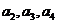 及
及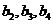 ,由此猜测
,由此猜测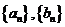 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明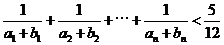 .
.
19.(12分)如图,平面ABEF ABCD,四边形ABEF与ABCD都是直角梯形,
ABCD,四边形ABEF与ABCD都是直角梯形,
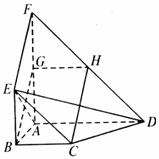

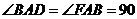 °,BC
°,BC 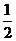 AD,BE
AD,BE 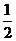 FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
(1)证明四边形BCHG是平行四边行.
(2)C、D、E、F四点是否共面?为什么?
(3)设AB=BE,证明平面ADE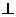 平面CDE.
平面CDE.
18.(12分)设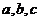 为正实数,
为正实数,
求证: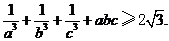 .
.
17. (12分)已知函数
(12分)已知函数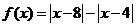 .
.
(1)作出函数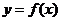 的图像.
的图像.
(2)解不等式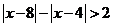 .
.
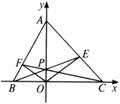
16.如图,在平面直角坐标系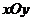 中,设三角形ABC的顶点分别为
中,设三角形ABC的顶点分别为
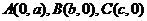 ;点
;点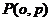 为线段 AO上的一点
为线段 AO上的一点
(异于端点),这里 为非零常数,设直线BP、CP分别
为非零常数,设直线BP、CP分别
与边AC、AB交于点E、F.某同学已正确求得直线OE的方程: 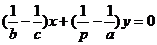 .请你完成直线OF的方程:
.请你完成直线OF的方程:
( )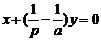 .
.
15. 已知
已知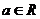 ,若关于
,若关于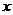 的方程
的方程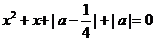
 有实根,则
有实根,则 的取值范围是 .
的取值范围是 .
13.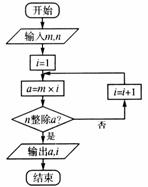 设
设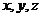 为正实数,满足
为正实数,满足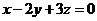 ,则
,则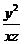 的最小值是
.
的最小值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com