
5.已知a>2,b>2,则a+b与ab的大小关系是__________.
4.“不等式a3+b3+c3≥3abc”成立的充要条件是 ( )
A.a+b+c≥0 B. a+b+c≥0,3abc≥0
C.a>0,b>0,c>0 D.a≥0, b≥0, c≥0
[填空题]
3.(2004湖北)若 ,则下列不等式①
,则下列不等式①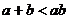 ;②
;②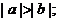 ③
③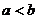 ;
;
④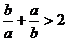 中,正确的不等式有 ( )
中,正确的不等式有 ( )
A.1个 B.2个 C.3个 D.4个
2.(2006江西)若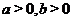 ,则不等式
,则不等式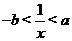 等价于( )
等价于( )
A.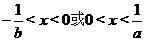 B.
B.
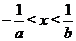
C.
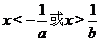 D.
D.
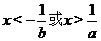
1.(2006浙江)“ ”是“
”是“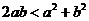 ”的 ( )
”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不允分也不必要条件
3.对于含参问题的大小比较要注意分类讨论.
同步练习 6.1不等式的性质
[选择题]
2.比较两数大小,一般用作差法。步骤:作差---变形(分解因式或配方)---判断符号
1.熟练掌握准确运用不等式的性质。
[例1]已知a<2,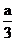 <b≤2a,c=b-2a,
<b≤2a,c=b-2a,
求c的取值范围.
解:∵b≤2a
∴c=b-2a≤0,
∴ b-4>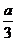 -2a=
-2a=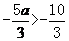 .
.
∴c的取值范围是: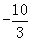 <c≤0.
<c≤0.
[例2]设f(x)=ax2+bx,且1≤f(-1) ≤2, 2≤f(1) ≤4 ,求f(-2)的取值范围
解:由已知1≤a-b≤2, ①, 2≤a+b≤4 ②
若将f(-2)=4a-2b用a-b与a+b,表示,则问题得解
设4a-2b=m(a-b)+n(a+b), (m,n为待定系数)
即4a-2b=(m+n)a-(m-n)b,
于是得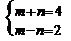 得:m=3, n=1
得:m=3, n=1
由①×3+②×1得5≤4a-2b≤10
即5≤f(-2)≤10,
另法:由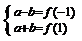 得
得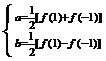
∴f(-2)=4a-2b=3 f(-1)+ f(1)……
◆特别提醒:常见错解:由①②解出a和b的范围,再凑出4a-2b的范围.错误的原因是a和b不同时接近端点值,可借且于线性规划知识解释.
[例3](1)设A=xn+x-n,B=xn-1+x1-n,当x∈R+,n∈N时, 比较A与B的大小.
(2)设0<x<1,a>0且a≠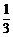 ,试比较|log3a(1-x)3|与|log3a(1+x)3|的大小.
,试比较|log3a(1-x)3|与|log3a(1+x)3|的大小.
解: (1)A-B=(xn+x-n)-(xn-1+x1-n)
=x-n(x2n+1-x2n-1-x)
=x-n[x(x2n-1-1)-(x2n-1-1)]
=x-n(x-1)(x2n-1-1).
由x∈R+,x-n>0,得
当x≥1时,x-1≥0,x2n-1-1≥0;
当x<1时,x-1<0,x2n-1<0,即
x-1与x2n-1-1同号.∴A-B≥0.∴A≥B.
(2)∵0<x<1,所以
①当3a>1,即a>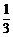 时,
时,
|log3a(1-x)3|-|log3a(1+x)3|
=|3log3a(1-x)|-|3log3a(1+x)|
=3[-log3a(1-x)-log3a(1+x)]
=-3log3a(1-x2).
∵0<1-x2<1,∴-3log3a(1-x2)>0.
②当0<3a<1,即0<a<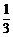 时,
时,
|log3a(1-x)3|-|log3a(1+x)3|
=3[log3a(1-x)+log3a(1+x)]
=3log3a(1-x2)>0.
综上所述,|log3a(1-x)3|>|log3a(1+x)3|.
◆提炼方法:(1)作差分解因式、配方或利用单调性,分类判断差式的符号.
[例4]已知函数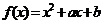 ,
,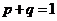 ,试比较
,试比较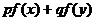 与
与 的大小.
的大小.
解 作差 -
-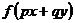
=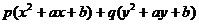
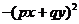
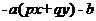
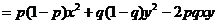
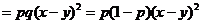
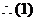 当
当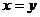 时,
时,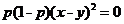 得
得
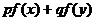 =
= 。
。
(2)当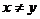 时,
时,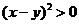 ,所以
,所以
①当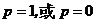 时,
时,
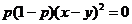 得
得
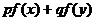 =
= 。
。
②当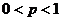 时,
时,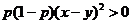 得
得
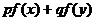 >
>
③当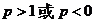 时,
时,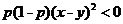 得
得
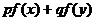 <
<
综上所述:当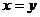 或
或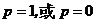 时
时
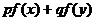 =
= 。
。
当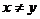 且
且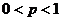 时
时
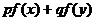 >
> 。
。
当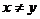 且
且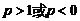 时
时
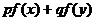 <
< 。
。
[研讨.欣赏]已知a>b>c,a+b+c=0方程ax2+bx+c=0的两个实根为x1,x2
(1) 证明:-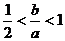 ;
;
(2) 若x12+x1x2+x22=1,求x12-x1x2+x22
解:(1)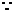 a>b>c,a+b+c=0,
a>b>c,a+b+c=0,
∴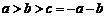
且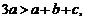 a>0,
a>0,
∴1>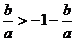 ,
, 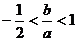
(2)(方法1) 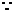 a+b+c=0
a+b+c=0
∴ ax2+bx+c=0有一根为1,
不妨设x1=1,则由x12+x1x2+x22=1可得x2(x2+1)=0,
而x2=x1x2= <0(3c<a+b+c=0),∴ x2=-1
<0(3c<a+b+c=0),∴ x2=-1
∴x12-x1x2+x22=3
(方法2) 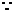 x1+x2=-
x1+x2=-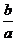 ,x1x2=
,x1x2=
由x12+x1x2+x22=(x1+x2)2- x1x2=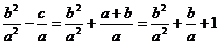 =1,
=1,
∴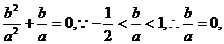
∴x12-x1x2+x22= x12+x1x2+x22-2x1x2=1-2x1x2=1+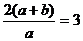
6.a>b>0,m>0,n>0,则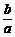 ,
,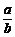 ,
,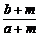 ,
,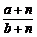 的由大到小的顺序是____________.
的由大到小的顺序是____________.
练习简答:1-4.CCCD; 5. ②与④; 6.特殊值法,答案: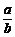 >
>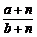 >
>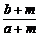 >
>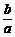
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com