
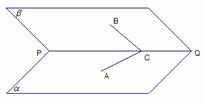
例1.已知二面角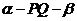 为
为 ,点
,点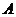 和
和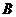 分别在平面
分别在平面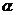 和平面
和平面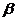 内,点
内,点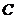 在棱
在棱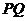 上
上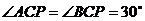 ,
,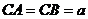 ,(1)求证:
,(1)求证: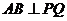 ;(2)求点
;(2)求点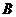 到平面
到平面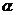 的距离;(3)设
的距离;(3)设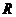 是线段
是线段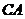 上的一点,直线
上的一点,直线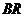 与平面
与平面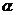 所成的角为
所成的角为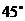 ,求
,求 的长
的长
(1)证明:作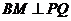 于
于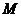 ,连接
,连接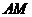 ,
,
 ∵
∵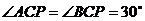 ,
,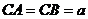 ,
,
∴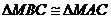 ,∴
,∴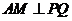 ,
,
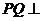 平面
平面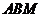 ,
,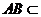 平面
平面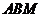 ,
,
∴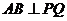 .
.
解:(2)作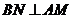 于
于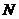 ,
,
∵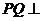 平面
平面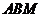 ,∴
,∴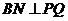 ,
,
∴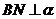 ,
, 是点
是点 到平面
到平面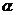 的距离,由(1)知
的距离,由(1)知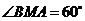 ,
,
∴ .∴点
.∴点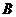 到平面
到平面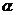 的距离为
的距离为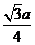 .
.
(2)连接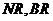 ,∵
,∵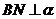 ,
,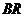 与平面
与平面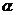 所成的角为
所成的角为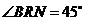 ,
,
 ,
,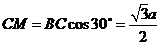 ,
,
∴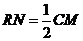 ,∵
,∵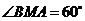 ,
,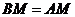 ,
,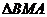 为正三角形,
为正三角形,
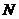 是
是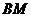 中点,∴
中点,∴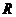 是
是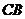 中点,∴
中点,∴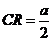 .
.
小结:求点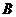 到平面
到平面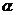 的距离关键是寻找点
的距离关键是寻找点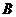 到
到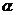 的垂线段.
的垂线段.
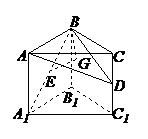 例2.在直三棱柱
例2.在直三棱柱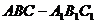 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,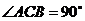 ,侧棱
,侧棱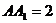 ,
,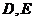 分别是
分别是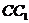 ,与
,与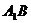 的中点,点
的中点,点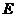 在平面
在平面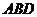 上的射影是
上的射影是 的重心
的重心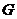 ,(1)求
,(1)求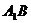 与平面
与平面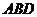 所成角的正弦值;(2)求点
所成角的正弦值;(2)求点 到平面
到平面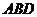 的距离.
的距离.
解:建立如图的空间直角坐标系,设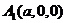 ,
,
则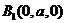 ,
,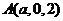 ,
,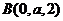 ,
,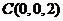 ,
,
∵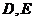 分别是
分别是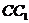 ,与
,与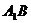 的中点,
的中点,
∴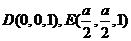 ,∵
,∵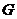 是
是 的重心,
的重心,
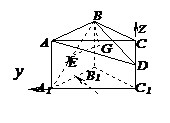
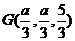 ,∴
,∴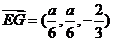 ,
,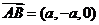 ,
,
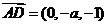 ,∵
,∵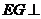 平面
平面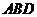 ,
,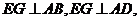
得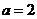 ,且
,且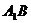 与平面
与平面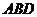 所成角
所成角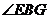 ,
,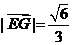 ,
,
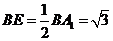 ,
,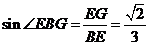 ,
,
(2)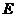 是
是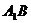 的中点,
的中点, 到平面
到平面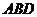 的距离等于
的距离等于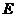 到平面
到平面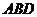 的距离的两倍,
的距离的两倍,
∵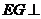 平面
平面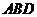 ,
, 到平面
到平面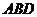 的距离等于
的距离等于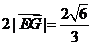 .
.
小结:根据线段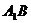 和平面
和平面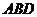 的关系,求点
的关系,求点 到平面
到平面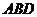 的距离可转化为求
的距离可转化为求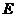 到平面
到平面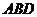 的距离的两倍.
的距离的两倍.
 例3.已知正四棱柱
例3.已知正四棱柱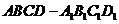 ,
,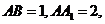 点
点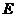 为
为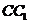 的中点,点
的中点,点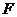 为
为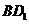 的中点,(1)证明:
的中点,(1)证明: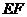 为异面直线
为异面直线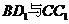 的公垂线;
的公垂线;
(2)求点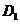 到平面
到平面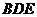 的距离.
的距离.
解:(1)以 分别为
分别为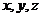 轴建立坐标系,
轴建立坐标系,
则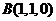 ,
,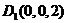 ,
,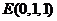 ,
,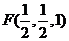 ,
,
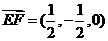 ,
,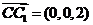 ,
, ,
,
∴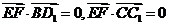 ,
,
∴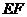 为异面直线
为异面直线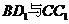 的公垂线.
的公垂线.
(2)设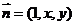 是平面
是平面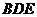 的法向量,∵
的法向量,∵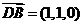 ,
,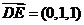
∴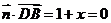 ,
,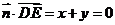 ,
,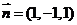 ,
,
点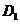 到平面
到平面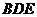 的距离
的距离 .
.
小结:由平面的法向量能求出点到这个平面的距离.
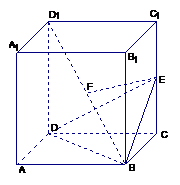
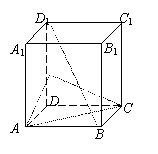
例4. 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥ D1B且面EAC与底面ABCD所成的角为45°,AB=a。(1)求截面EAC的面积;(2)求异面直线A1B1与AC之间的距离。
4.已知二面角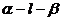 为
为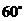 ,平面
,平面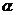 内一点
内一点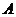 到平面
到平面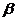 的距离为
的距离为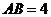 ,则
,则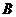 到平面
到平面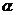 的距离为
的距离为 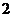 .
.
3.已知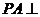 矩形
矩形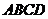 所在平面,
所在平面,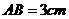 ,
,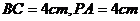 ,则
,则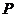 到
到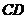 的距离为
的距离为 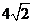
 ,
,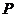 到
到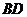 的距离为
的距离为 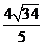
 .
.
2.在四面体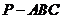 中,
中,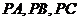 两两垂直,
两两垂直,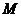 是面
是面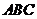 内一点,
内一点,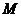 到三个面
到三个面
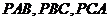 的距离分别是
的距离分别是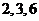 ,则
,则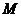 到
到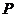 的距离是
(
的距离是
( 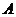 )
)

1.在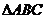 中,
中,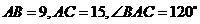 ,
,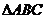 所在平面外一点
所在平面外一点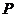 到三顶点
到三顶点
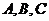 的距离都是
的距离都是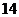 ,则
,则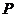 到平面
到平面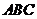 的距离是
(
的距离是
( 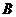 )
)
4.异面直线间的距离: .
3.两个平面的距离: .
2.直线到平面的距离: .
1.点到平面的距离: .
33、求4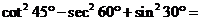 ______。
______。
答案: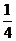
解析:原式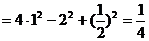
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com