
例1 已知函数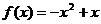 的图象上的一点
的图象上的一点 及临近一点
及临近一点
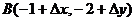 则
则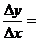 .
.
解: 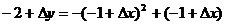
∴
例2 求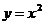 在
在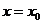 附近的平均变化率.
附近的平均变化率.
解: 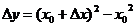
所以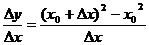
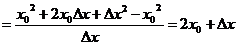
所以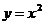 在
在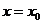 附近的平均变化率为
附近的平均变化率为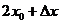
(二)平均变化率概念
1.上述问题中的变化率可用式子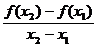 表示,
表示,
称为函数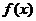 从
从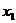 到
到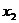 的平均变化率.
的平均变化率.
2. 若设
若设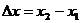 ,
, 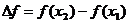 (这里
(这里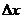 看作是对于
看作是对于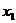 的一个“增量”可用
的一个“增量”可用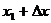 代替
代替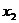 ,同样
,同样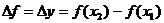 )
)
则平均变化率为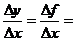
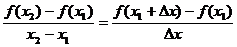
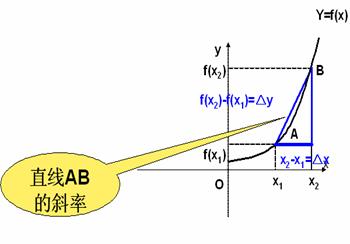
思考: 观察函数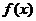 的图象
的图象
平均变化率
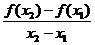 表示什么?
表示什么?
(一)问题提出
问题1 气球膨胀率
我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢?
气球的体积 (单位:
(单位: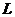 )与半径
)与半径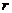 (单位:
(单位: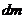 )之间的函数关系是
)之间的函数关系是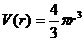

如果将半径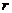 表示为体积
表示为体积 的函数,那么
的函数,那么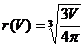
分析: 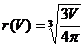
(1)当 从
从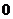 增加到
增加到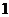 时,气球半径增加了
时,气球半径增加了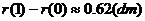
气球的平均膨胀率为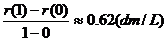
(2)当 从
从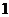 增加到
增加到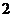 时,气球半径增加了
时,气球半径增加了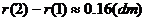
气球的平均膨胀率为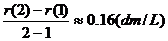
可以看出,随着气球体积逐渐增大,它的平均膨胀率逐渐变小了.
思考: 当空气容量从V1增加到V2时,气球的平均膨胀率是多少?
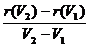
 问题2 高台跳水
问题2 高台跳水
在高台跳水运动中,运动员相对于水面的高度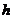 (单位:
(单位: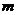 )与起跳后的时间
)与起跳后的时间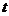 (单位:
(单位: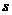 )存在函数关系
)存在函数关系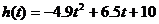 .如何用运动员在某些时间段内的平均速
.如何用运动员在某些时间段内的平均速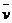 度粗略地描述其运动状态?
度粗略地描述其运动状态?
思考计算: 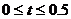 和
和 的平均速度
的平均速度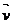
在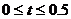 这段时间里,
这段时间里,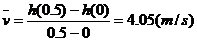
在 这段时间里,
这段时间里,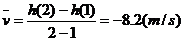
探究: 计算运动员在 这段时间里的平均速度,并思考以下问题:
这段时间里的平均速度,并思考以下问题:
(1)运动员在这段时间内使静止的吗?
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
探究过程: 如图是函数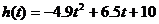 的图像,
的图像,
结合图形可知,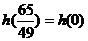 ,所以
,所以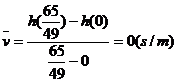
虽然运动员在 这段时间里的平均速度为
这段时间里的平均速度为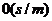 ,
,
但实际情况是运动员仍然运动,并非静止,
可以说明用平均速度不能精确描述运动员的运动状态.
导数是微积分的核心概念之一它是研究函数增减、变化快慢、最大(小)值等问题最一般、最有效的工具.
导数研究的问题即变化率问题:研究某个变量相对于另一个变量变化的快慢程度.
为了描述现实世界中运动、过程等变化着的现象,在数学中引入了函数,随着对函数的研究,产生了微积分,微积分的创立以自然科学中四类问题的处理直接相关:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com