
4、人造卫星、宇宙速度:
(1)人造卫星分类(略):其中重点了解同步卫星
(2)宇宙速度:(弄清第一宇宙速度与发卫星发射速度的区别)
例题分析
例1、利用下列哪组数据,可以计算出地球质量:(A B)
A、已知地球半径和地面重力加速度
B、已知卫星绕地球作匀速圆周运动的轨道半径和周期
C、已知月球绕地球作匀速圆周运动的周期和月球质量
D、已知同步卫星离地面高度和地球自转周期
本例从各方面应用万有引力提供向心力来求出不同条件下地球(行星)质量表达式。
例2、某同步卫星相对地面是静止的,已知地球半径是6400km,地面重力加速度g=9.8m/s2。求(1)同步卫星离地面高度h;(2)同步卫星线速度v(36000000m;3100m/s)
拓展:同步通讯卫星运动的轨道平面应在地球上空什么位置?
例3、地球同步卫星到地心的距离r可由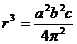 求出,已知式中a的单位是m,b的单位是s,c的单位是m/s2,则:(AD)
求出,已知式中a的单位是m,b的单位是s,c的单位是m/s2,则:(AD)
A、a是地球半径,b是地球自转的周期,C是地球表面处的重力加速度;
B、a是地球半径。b是同步卫星绕地心运动的周期,C是同步卫星的加速度;
C、a是赤道周长,b是地球自转周期,C是同步卫星的加速度
D、a是地球半径,b是同步卫星绕地心运动的周期,C是地球表面处的重力加速度。
解析:由万有引力定律导出人造地球卫星运转半径的表达式,再将其与题给表达式中各项对比,以明确式中各项的物理意义。
3、万有引力定律的应用主要涉及两个方面:
(1)测天体的质量及密度:(万有引力全部提供向心力)
由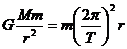 得
得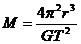
又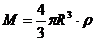 得
得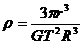
(2)行星表面重力加速度、轨道重力加速度问题:(重力近似等于万有引力)
表面重力加速度: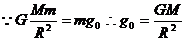
轨道重力加速度: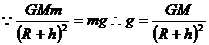
2、天体运动的研究:天体运动可看成是匀速圆周运动--其引力全部提供向心力
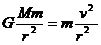
讨论:(1)由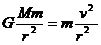 可得:
可得: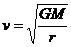 r越大,V越小。
r越大,V越小。
(2)由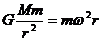 可得:
可得: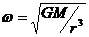 r越大,ω越小。
r越大,ω越小。
(3)由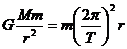 可得:
可得: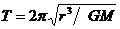 r越大,T越大。
r越大,T越大。
(4)由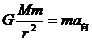 可得:
可得: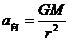 r越大,a向越小。
r越大,a向越小。
目的要求
复习万有引力定律、宇宙速度、人造卫星及应用
知识要点
1、万有引力定律:(1687年)
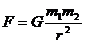
适用于两个质点或均匀球体;r为两质点或球心间的距离;G为万有引力恒量(1798年由英国物理学家卡文迪许利用扭秤装置测出)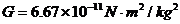
4、处理圆周运动动力学问题般步骤:
(1)确定研究对象,进行受力分析;
(2)建立坐标系,通常选取质点所在位置为坐标原点,其中一条轴与半径重合;
(3)用牛顿第二定律和平衡条件建立方程求解。
例题分析
 例1、物体质量为m,在下列各种情况中作匀速圆周运动,半径为R,周期为T,分析其向心力来源,列出动力学表达式:(1)置于水平转动的圆盘上随之一起作圆周运动;(2)置于竖直转动圆筒内壁的物体,随之一起转动;(3)飞机在空中水平匀速转圈。
例1、物体质量为m,在下列各种情况中作匀速圆周运动,半径为R,周期为T,分析其向心力来源,列出动力学表达式:(1)置于水平转动的圆盘上随之一起作圆周运动;(2)置于竖直转动圆筒内壁的物体,随之一起转动;(3)飞机在空中水平匀速转圈。
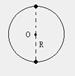 例2、如图所示,用长为l的轻绳一端固定在O点,另一端拴质量为m的小球,并令小球在竖直平面内绕O点作圆周运动,求小球在圆周的最高点时速度和拉力特点及最低点时速度和拉力特点?
例2、如图所示,用长为l的轻绳一端固定在O点,另一端拴质量为m的小球,并令小球在竖直平面内绕O点作圆周运动,求小球在圆周的最高点时速度和拉力特点及最低点时速度和拉力特点?
拓展:如把轻绳改为轻杆,分析速度和拉力特点
拓展:假如小球能在竖直平面内作全圆周运动,
求最高点和最低点的拉力之差(6mg)
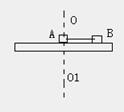
例3、如图所示,两个相同的木块A和B放在转盘上,木块与转盘的最大摩擦力是重力的K倍,用长为L的细线连接A和B。(1)若A放在轴心,B放在距轴心L处,它们不发生相对滑动,角速度ω的取值范围?(2)若A放在离轴心R1处,B放在同侧距轴心R2处(R2-R1=L),要使它们不发生相对滑动,角速度ω的最大值是多少?(3)若A放在距轴心R1处,B放在异侧距轴心R2处(R2+R1=L),要使它们不发生相对滑动,角速度ω的最大值为多少?
3、向心力表达式:

2、变速圆周运动特点:

 (1)速度大小变化 有切向加速度;速度方向改变
有向心加速度。故合加速度不一定指向圆心。
(1)速度大小变化 有切向加速度;速度方向改变
有向心加速度。故合加速度不一定指向圆心。
(2)合外力不一定全提供向心力,合外力不一定指向圆心。
目的要求
圆周运动向心力,牛顿第二定律的特定应用。
知识要点
1、匀速圆周运动特点:

 (1)速度大小不变 无切向加速度;速度方向改变 有向心加速度a=
(1)速度大小不变 无切向加速度;速度方向改变 有向心加速度a=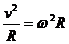
(2)合外力必提供向心力
2、描述匀速圆周运动的有关量及它们的关系:
(1)、线速度:
(2)、角速度:
(3)、周期:
(4)、频率:
(5)、向心加速度:
虽然匀速圆周运动线速度大小不变,但方向时刻改变,故匀速圆周运动是变速运动;向心加速度大小不变但方向时刻改变(始终指向圆心),故匀速圆周运动是一种变加速运动。
例题分析
例1、如图所示为皮带传动装置,右轮半径为r,a为它边缘的一点,左侧是大轮轴,大轮半径为4r,小轮半径为2r。b为小轮上一点,它到小轮中心距离为r,c、d分别位于小轮和大轮的边缘上,若在传动中不打滑,则:( C D )
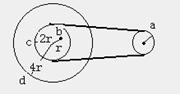 A、a点与b点线速度大小相等;
A、a点与b点线速度大小相等;
B、a点与b点角速度大小相等;
C、a点与c点线速度大小相等;
D、a点与d点向心加速度大小相等;
本例主要考查线速度、角速度、向心加速度概念,同时抓住两个核心:若线速度一定时,角速度与半径成反比;若角速度一定,线速度与半径成正比。
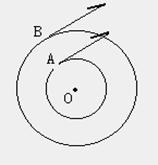 例2、如图所示,A、B两质点绕同一圆心按顺时针方向作匀速圆周运动,A的周期为T1,B的周期为T2,且T1<T2,在某时
例2、如图所示,A、B两质点绕同一圆心按顺时针方向作匀速圆周运动,A的周期为T1,B的周期为T2,且T1<T2,在某时
刻两质点相距最近,开始计时,问:
(1)何时刻两质点相距又最近?
(2)何时刻两质点相距又最远?
分析:选取B为参照物。
(1) AB相距最近,则A相对于B转了n转,
其相对角度△Φ=2πn
相对角速度为ω相=ω1-ω2经过时间:
t=△Φ/ω相=2πn/ω1-ω2=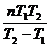 (n=1、2、3…)
(n=1、2、3…)
(2)AB相距最远,则A相对于B转了n-1/2转,
其相对角度△Φ=2π(n-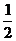 )
)
经过时间:t=△Φ/ω相=(2n-1)T1T2/2(T2-T1)(n=1、2、3…)
本题关键是弄清相距最近或最远需通过什么形式来联系A和B的问题,巧选参照系是解决这类难题的关键。
目的要求
学会利用描述匀速圆周运动有关物理量分析有关事例
知识要点
1、物体运动的轨迹是圆周或是圆周一部分叫圆周运动;作圆周运动的物体相等时间内通过的弧长相等称为匀速圆周运动。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com