2.(04全国卷Ⅱ21)放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系,和物块速度v与时间t的关系如图所示,取重力加速度g=10 m/s2.由此两图线可以求得物块的质量m和物块与地面之间的动摩擦因数μ分别为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A.m=0.5 kg,μ=0.4　　　 B.m=1.5 kg,μ=　　　 C.m=0.5 kg,μ=0.2　　 D.m=1 kg,μ=0.2

　 答案　 A

　 解析　 本题考查读图能力,即从图象中获取信息、筛选信息、利用信息解决问题的能力.正确理解图线表示的意义(特别是突变点表示的意义)是解答本题的关键.由图象可知,在4-6秒内,物体做匀速运动,此时F=2 N,由平衡条件知,2- f =0.在2-4秒内物体做匀加速运动,加速度a=2 m/s2,此时F=3 N,由牛顿第二定律,2-,f =μmg,可解得m=0.5 kg,μ=0.4. 故选项A正确.

1.(04广东综合能力测试32)如图所示,三个完全相同的物块,1、2、3放在水平桌上,它们与桌面间的动摩擦因数都相同,现用大小相同的外力F沿图示方向分别作用在1和2上,用F的外力沿水平方向作用在3上,使三者做加速运动,令a1、a2、a3分别代表物块1、2、3的加速度,则　　　　　　　 　　　　　　　　　　　　　　　　　 　(　　 )

A.a1=a2=a3　　　 B.a1=a2,a2 > a3　　　 C.a1 > a2,a2 < a3　　　 D.a1 > a2,a2 > a3

　 答案　　 C

　 解析　　 由牛顿定律F合=ma

　 a1=

=

a2=

=

a3=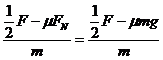

比较上述三式可知a1 > a2,a2 < a3,故选C.

15.(04天津理综24)质量m=1.5 kg的物块(可视为质点)在水平恒力F作用下,从水平面上A点由静止开始运动,运动一段距离撤去该力,物块继续滑行,t=2.0 s停在B点,已知A、B两点间的距离s=5.0 m,物块与水平面间的动摩擦因数μ=0.20.求恒力F多大.(g=10 m/s2)

　 答案　　 F=15 N

　 解析　 设撤去力F前物块的位移为s1,撤去力F时物块速度为v,物块受到的滑动摩擦力F1=μmg

　 对撤去力F后物块滑动过程应用动量定理得-F1t=0-mv

　 由运动学公式得 s-s1=

　 对物块运动的全过程应用动能定理Fs1-F1s=0

　 由以上各式得F=

　 代入数据得　 F=15 N

题　组　二

14.(06全国卷Ⅱ24)一质量为m =40 kg的小孩站在电梯内的体重计上.电梯从

t =0时刻由静止开始上升,在0到6 s内体重计示数F的变化如图所示.试问：

在这段时间内电梯上升的高度是多少？取重力加速度g=10 m/s2.

答案　　 9 m

解析　 由题图可知,在t =0到t1=2 s的时间内,体重计的示数大于mg,故电梯应做向上的加速运动.设在这段时间内体重计作用于小孩的力为f1,电梯及小孩的加速度为a1,由牛顿第二定律,

得f1-mg=ma1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

在这段时间内电梯上升的高度　h1=a1t12　　　　　　　　　　　　 ②

在t1到t2=5 s的时间内,体重计的示数等于mg,故电梯应做匀速上升运动,速度为t1时刻电梯的速度,即

v1=a1t1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

在这段时间内电梯上升的高度

h2=v1(t2-t1)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

在t2到t3=6 s的时间内,体重计的示数小于mg,故电梯应做向上的减速运动.设这段时间内体重计作用于小孩的力为f2,电梯及小孩的加速度为a2,由牛顿第二定律,得

mg-f2=ma2　　　　　　　　　　　　　　　　　　　　 ⑤

在这段时间内电梯上升的高度　

h3=v1(t3-t2)-a2(t3-t2)2　　　　　　　　　　　　　　 ⑥

电梯上升的总高度　

h=h1+h2+h3　　　　　　　　　　　　　　　　　　　　 ⑦

由以上各式和题文及题图中的数据,解得h=9 m

13.(07江苏15) 直升机沿水平方向匀速飞往水源取水灭火,悬挂着m=500 kg空箱的悬索与竖直方向的夹角

θ1=45°.直升机取水后飞往火场,加速度沿水平方向,大小稳定在a =1.5 m/s2时,悬索与竖直方向的夹角

θ2=14°.如果空气阻力大小不计,且忽略悬索的质量,试求水箱中水的质量M.(取重力加速度g =10 m/s2;

sin 14°≈0.242;cos 14°≈0.970)

答案　 4.5×103kg

解析　 直升机取水时,水箱受力平衡

T1sinθ1- f =0　　　　　　　　　　　　　　　　　　　　　　　　 　 ①

T1cosθ1-mg=0　　　　　　　　　　　 　　　　②

由①②得f =mgtanθ1　　　　　　　　　　　　 ③

直升机返回时,由牛顿第二定律　

T2sinθ2- f =(m+M)a　　　　　　　　　　　　 ④

T2cosθ2-(m+M)g=0　　　　　　　　　　　　 ⑤

由③④⑤得,水箱中水的质量M=4.5×103 kg

12.(07上海19B) 固定光滑细杆与地面成一定倾角,在杆上套有一个光滑小环,小

环在沿杆方向的推力F作用下向上运动,推力F与小环速度v随时间变化规律

如图所示,取重力加速度g=10 m/s2.求小环的质量m;细杆与地面间的倾角α.　

答案　 (1)1kg　 (2)30°

解析　 由v-t图象可解得：a=,前2 s内,由牛顿第二定律得:F-mgsinα=ma.　

2s满足:F=mgsinα代入数据可解得：m=1 kg,α=30°

11.(07上海21)如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒钟通过速度传感器测量物体的瞬时速度,下表给出了部分测量数

据.(重力加速度g =10 m/s2)求:

(1)斜面的倾角落 α

(2)物体与水平面之间的动摩擦因数μ

(3) t =0.6 s 时的瞬时速度 v

答案　(1)α=30°　 (2)μ=0.2　 (3)2.3 m/s

解析　 (1)物体在光滑斜面上运动时,做匀速直线运动,由前三列数据可求物体在斜面上运动时的加速度,则

,在斜面上运动时重力的分力提供加速度,即:a1=gsinα,解得:α=30°.

物体在水平面上做匀速直线运动,由后两列数据可求得物体在水平面上运动时的加速度

a2=负号表示水平面上的加速度与物体运动速度方向相反.

由a2=μg得:μ=

设物体在斜面上运动时间为t ,则物体到达斜面末端的速度v1=a1t=5t ,然后物体又做匀速直线运动,又经

过(1.2-t ) s 速度变为1.1 m/s,则a1t-a2(1.2-t)=v2,

代入数据解得t =0.5 s ,则t＇=0.6 s时物体在水平面上,其速度v=a1t-a2(t＇-t )=5×0.5 m/s-2×0.1 m/s=2.3m/s .

10.(06全国卷Ⅰ24)一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送之间的动摩擦因数为μ.初始时,传送带与煤块都是静止的,现让传送带以恒定的加速度a0开始运动,当其速度到达v0后,便以此速度做匀速运动.经过一段时间,煤块在传送带上留下了一段黑色痕迹后,相对于传送带不再滑动,求此黑色痕迹的长度.

　 答案　　 l =

　 解析　　 根据“传送带上有黑色痕迹”可知,煤块与传送带之间发生了相对滑动,煤块的加速度a小于传送带的加速度a0,根据牛顿第二定律,可得a=μg

　 设经历时间t,传送带由静止开始加速到速度等于v0,煤块则由静止加速到v,有v0=a0t　　 v =at

　 由于a<a0,故v<v0,煤块继续受到滑动摩擦力的作用.再经过时间t＇,煤块的速度由v增加到v0,有v0=v+at＇

　 此后,煤块与传送带运动速度相同,相对于传送带不再滑动,不再产生新的痕迹.

　 设在煤块的速度从0增加到v0的整个过程中,传送带和煤块移动的距离分别为s0和s,有s0=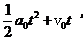

　 s =,传送带上留下的黑色痕迹的长度　 l =s0-s

　 由以上各式得l =

9.(04全国卷Ⅲ19)如图, 在倾角为α的固定光滑斜面上,有一用绳子拴着的长

木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断

开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜

面下滑的加速度为　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )　

?A.sinα　　 ?　 B.gsinα?　　　　　 C.gsinα　　　 ?　 D.2gsinα

答案 ?C

解析　 对猫受力分析如图(a)由平衡条件:Ff =mgsinα 　　　　　①

对木板受力分析如图(b) 由牛顿第二定律:Ff′+2mgsinα=2ma　 ②

又由牛顿第三定律:Ff′=Ff　　　　　　　　　　　　　　　　　 ③

由①②③得a = gsinα

8.(05北京春季理综20)如图所示,一个盛水的容器底部有一个小孔.静止时用手指堵住小

孔不让它漏水,假设容器在下述几种运动过程中始终保持平动,且忽略空气阻力,则　 (　 )　

?A.容器自由下落时,小孔向下漏水　

?B.将容器竖直向上抛出后,容器向上运动时,小孔向下漏水，容器向下运动时,小孔不向下漏水　

?C.将容器水平抛出后,容器在运动中小孔向下漏水　

?D.将容器斜向上抛出后,容器在运动中小孔不向下漏水　

答案　 D

解析　 当容器自由落体时,水对容器底部无压力,且水和容器的运动情况相同,因此小孔不会漏水.