5.(09·上海物理·4)做简谐振动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1/2，则单摆振动的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 C　 )

A．频率、振幅都不变　　　　　　 B．频率、振幅都改变

C．频率不变、振幅改变　 　　 D．频率改变、振幅不变

解析：由单摆的周期公式，可知，单摆摆长不变，则周期不变，频率不变；振幅A是反映单摆运动过程中的能量大小的物理量，由可知，摆球经过平衡位置时的动能不变，因此振幅改变，所以C正确。

4.(09·北京·17)一简谐机械波沿x轴正方向传播，周期为T，波长为。若在x=0处质点的振动图像如右图 所示，则该波在t=T/2时刻的波形曲线为　　　　　　　　　　　　　　 (　 A　 )

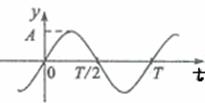
解析：从振动图上可以看出x=0处的质点在t=T/2时刻处于平衡位置，且正在向下振动，四个选项中只有A图符合要求，故A项正确。

3.(09·北京·15)类比是一种有效的学习方法，通过归类和比较，有助于掌握新知识，提高学习效率。在类比过程中，既要找出共同之处，又要抓住不同之处。某同学对机械波和电磁波进行类比，总结出下列内容，其中不正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 D　 )

A．机械波的频率、波长和波速三者满足的关系，对电磁波也适用

B．机械波和电磁波都能产生干涉和衍射现象

C．机械波的传播依赖于介质，而电磁波可以在真空中传播

D．机械波既有横波又有纵波，而电磁波只有纵波

解析：波长、波速、频率的关系对任何波都是成立的，对电磁波当然成立，故A选项正确；干涉和衍射是波的特性，机械波、电磁波都是波，这些特性都具有，故B项正确；机械波是机械振动在介质中传播形成的，所以机械波的传播需要介质而电磁波是交替变化的电场和磁场由近及远的传播形成的，所以电磁波传播不需要介质，故C项正确；机械波既有横波又有纵波，但是电磁波只能是横波，其证据就是电磁波能够发生偏振现象，而偏振现象是横波才有的， D项错误。故正确答案应为D。

2.(09·全国卷Ⅱ·14)下列关于简谐振动和简谐波的说法，正确的是　　　　　　　 (　 AD　 )

A．媒质中质点振动的周期一定和相应的波的周期相等

B．媒质中质点振动的速度一定和相应的波的波速相等

C．波的传播方向一定和媒质中质点振动的方向一致

D．横波的波峰与波谷在振动方向上的距离一定是质点振幅的两倍

解析：本题考查机械波和机械振动.介质中的质点的振动周期和相应的波传播周期一致A正确.而各质点做简谐运动速度随时间作周期性的变化,但波在介质中是匀速向前传播的,所以不相等,B错.对于横波而言传播方向和振动方向是垂直的,C错.根据波的特点D正确。

1.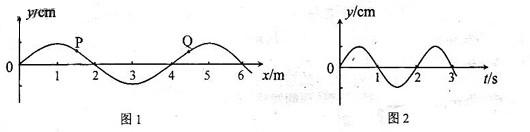(09·全国Ⅰ·20)一列简谐横波在某一时刻的波形图如图1所示，图中P、Q两质点的横坐标分别为x=1.5m和x=4.5m。P点的振动图像如图2所示。

在下列四幅图中，Q点的振动图像可能是　　　　　　　　　　　　　　 ( BC )

解析：本题考查波的传播.该波的波长为4m.,PQ两点间的距离为3m..当波沿x轴正方向传播时当P在平衡位置向上振动时而Q点此时应处于波峰,B正确.当沿x轴负方向传播时,P点处于向上振动时Q点应处于波谷,C对。

(1)空气中的声波是纵波．能在空气、液体、固体中传播．在通常情况下在空气中为340m／s，随介质、温度改变而变．

(2)人耳听到声波的频率范围：20 Hz ---20000 Hz.

(3)能够把回声与原声区分开来的最小时间间隔为0.1s

(4)声波亦能发生反射、折射、干涉和衍射等现象．声波的共振现象称为声波的共鸣．

(5)次声波：频率低于20 Hz的声波．

(6)超声波：频率高于20000 Hz的声波．

应用：声呐、探伤、打碎、粉碎、诊断等．

(7)声音的分类①乐音：好听悦耳的声音．乐音的三要素：音调(基音的频率的高低)、响度(声源的振幅大小)、音品(泛音的多少，泛音的频率和振幅共同决定的)．声强：单位时间内通过垂直于声波传播方向单位面积的能量．②噪声：嘈杂刺耳的声音，是妨碍人的正常生活和工作的声音．噪声已列为国际公害．

[例9]如果声源、听者和障碍物都在同一直线上，声源位于听者和障碍物之间，离听者12m，离障碍物34m，已知声音在空气中的传播速度340m/s，听者是否能把原来的声音和回声区分开来？

[解析]人耳能分外间隔大小0.1s的两个声音，图中S为声源，A为听者，O为障碍物，当声波直接传到人耳时，经历时间tl＝SA/v……①，当声波传到障碍物反射到人耳时，经历时间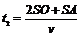………②，直接传到人耳的声音与回声之间的时间差Δt=t₂－t₁，即Δt=2SO/v＝0．2s。Δt＞0．1s，人耳可以区分

规律方法

试题展示

6．多普勒效应

(1)由于波源和观察者之间有相对运动，使观察者感到频率发生变化的现象．实质是：波源的频率没有变化，而是观察者接收到的频率发生了变化．

(2)多普勒效应的产生原因

观察者接收到的频率等于观察者在单位时间内接收到的完全波的个数．当波以速度v通过接收者时，时间t内通过的完全波的个数为N=vt/λ，因而单位时间内通过接收者的完全波的个数，即接收频率f　　　　 v/λ．

若波源不动，观察者朝向波源以速度V₂运动，由于相对速度增大而使得单位时间内通过观察者的完全波的个数增多，即，可见接收频率增大了.同理可知，当观察者背离波源运动时，接收频率将减小．

若观察者不动，波源朝向观察者以速度v₁运动，由于波长变短为λ^/=λ－v₁T，而使得单位时间内通过观察者的完全波的个数增多，即，可见接收频率亦增大，同理可知，当波源背离观察者运动时，接收频率将减小．

注：发生多普勒效应时，波源的真实率不发生任何变化，只是观察者接收到的频率发生了变化．

(3)相对运动与频率的关系

①波源与观察者相对静止：观察者接收到的频率等于波源的频率．

②波源与观察者相互接近：观察者接收到的频率增大．

③波源与观察者相互远离：观察者接收到的频率减小．

[例8]一机车汽笛频率为650Hz，机车以v=15m/s的速度观察者驶来，设空气中的声速是V=340m/s，观察者听到的声音频率为多少？

解答：机车静止时，汽笛声的波长为λ，由于机车(波源)向观察者运动，波长应减小vT，则单位时间内通过观察者的波数变为

即观察者听到的声音频率变大了，音调变高了。

5.驻波:两列沿相反方向传播的振幅相同、频率相同的波叠加时，形成驻波．

(1)波节：始终静止不动的点．

(2)波腹：波节与波节之间振幅最大的点．

(3)驻波-特殊的干涉现象:波源特殊;波形特殊

说明：驻波与行波的区别．

　①物理意义不同：驻波是两列波的特珠干涉现象，行波是一列波在介质中的传播．

②质点的振动情况不同：在行波中各个质点作振格相同的简谐运动，在驻波中各个质．点作振幅不同的简谐运动；处于波腹位置的质点振幅最大；处于波节位置的质点振幅等于零；其他一些质点的振幅也不相同，但都比波腹处质点的振幅小．

③波形不同：行波波形经过一段时间，波形向前“平移”，而驻波波形并不随时间发生平移，只是各质点的振动位移发生变化而已．

4.波的叠加与波的干涉

(1)波的叠加原理：在两列波相遇的区域里，每个质点都将参与两列波引起的振动，其位移是两列波分别引起位移的矢量和．相遇后仍保持原来的运动状态．波在相遇区域里，互不干扰，有独立性．

[例1]一个波源在绳的左端发出半个波①，频率为f₁，振幅为A₁；同时另一个波源在绳的右端发出半个波②，频率为f₂，振幅为A₂， P为两波源的中点，由图6-18可知，下述说法错误的是(　　　　 )

　　 A．两列波同时到达两波源的中点P

B．两列波相遇时， P点波峰值可达A₁+A₂ 　　

C．两列波相遇后，各自仍保持原来的波形独立传播

　　 D、两列波相遇时，绳上的波峰可达A₁+A₂的点只有一点，此点在P点的左侧

　　 解析：因两列波在同一介质(绳)中传播，所以波速相同，由图可知 λ₁＞λ₂，说明它们的波峰高P点距离不等，波同时传至P点，波峰不会同时到P点，所以P点波峰值小于A₁+ A₂．两列波波峰能同时传到的点应在P点左侧，所以A，D正确，B错误，又由波具有独立性，互不干扰，所以C正确．答案：B

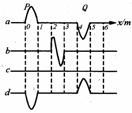[例2]一波源在绳子的左瑞发生波P．另一波源在同一根绳子右端发生波Q，波速为lm／s．在t＝0时绳上的波形如图中的a所示，根据波的叠加原理，以下判断正确的是(　 )

　A．当t＝2s时．波形图如b图．t＝4s时．波形图如c图；

　B．当t＝2s时，波形图如 b图，t＝4s时，波形图如d图　　

　C．当 t＝2s时，波形图如C图，t＝4s时，波形图如b图；

　D．当 t＝2s时，波形图如 C图，t=4s时，波形图如 d图　

解析:由图中的所示的图形来看，b图肯定是不正确的，因为波在同一媒质中传播时的波长是不变，而b图中波长发生了变化，所以选项内容中凡涉及到了b图的情况肯定是不正确的，本题4个选项中只有D选项没有涉及到b图，所以D选项肯定正确．从波的叠加角度来分析，在t＝2s时，两列波均传播了2m，它们刚好重合，由于它们是波峰和波谷相遇，所以叠加的结果是相遇后的质点位移均为零，C图是正确的，当t＝4s时，两列波均传播了4m的距离，相当于在a图的位置上互换，d图是正确的．所以D选项正确．

点评：本题的关键是扣住在同一媒质中，波传播过程中波形不变以及传播的距离与时间的关系．

[例3]两列简谐波均沿x轴传播，传播速度的大小相等，其中一列沿x轴正方向传播，如图32中实线所示。一列波沿x负方向传播，如图32中虚线所示。这两列波的频率相等，振动方向均沿y轴，则图中x=1,2,3,4,5,6,7,8各点中振幅最大的是x=　　　　　 的点，振幅最小的是x=　　　　　　 的点。

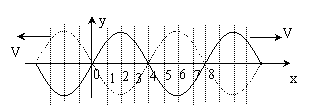解析:对于x=4、8的点，此时两列波引起的位移的矢量和为零，但两列波引起的振动速度的矢量和最大，故应是振动最强的点，即振幅最大的点。对于x=2和6的点，此时两列波引起的位移矢量和为零，两列波引起的振动速度的矢量和也为零，故应是振动最弱的点，即振幅最小的点。

　(2)波的干涉:

①条件：频率相同的两列同性质的波相遇．

②现象：某些地方的振动加强，某些地方的振动减弱，并且加强和减弱的区域间隔出现，加强的地方始终加强，减弱的地方始终减弱，形成的图样是稳定的干涉图样．

说明：①加强、减弱点的位移与振幅．

加强处和减弱处都是两列波引起的位移的矢量和，质点的位移都随时间变化，各质点仍围烧平衡位置振动，与振源振动周期相同．

加强处振幅大，等于两列波的振幅之和，即A=A₁ +A₂,质点的振动能量大，并且始终最大．

减弱处振幅小，等于两列波的振福之差，即A=∣A₁－A₂∣,质点振动能量小，并且始终最小，若A₁=A₂，则减弱处不振动．

加强点的位移变化范围： 一∣A₁ +A₂∣-∣A₁ +A₂∣

减弱点位移变化范围：一∣A₁－A₂∣-∣A₁－A₂∣

②干涉是波特有的现象．

③加强和减弱点的判断．

波峰与波峰(波谷与波谷)相遇处一定是加强的，并且用一条直线将以上加强点连接起来，这条直线上的点都是加强的；而波峰与波谷相遇处一定是减弱的，把以上减弱点用直线连接起来，直线上的点都是减弱的．加强点与减弱点之间各质点的振幅介于加强点与减弱点振幅之间．

当两相干波源振动步调相同时，到两波源的路程差Δs是波长整数倍处是加强区．而路程差是半波长奇数倍处是减弱区．

任何波相遇都能叠加，但两列频率不同的同性质波相遇不能产生干涉．

[例4]如图所示，在坐标xoy的y轴上有两个相同的波源A、B，它们激起水波波长为2m，A、B的坐标分别为(0，2m)和(0，5m)．在x轴上从－∞到十∞范围内两列波叠加相减弱的点的个数为多少个？

[解析]在X轴上任取点C，连接CA、CB．如图所示，由图可知CB－CA≤AB＝3m(由三角形任意两边之差小于第三边原理得出左式)，所以(CB－CA)的值可以取lm、2m、3m．而A、B两波源激起的水波波长为2m，则只有当(CB－CA)值为半波长的奇数倍时，两列波相遇才是减弱的，故取lm、3m时两列波叠加后是减弱的，由于是在x轴上从－∞到十∞范围内寻找，以及关于y轴对称的关系，故减弱点共有3个．

[例5]两列振动情况完全相同的振源。S₁和s₂在同一个介质中形成机械波。某时刻两列波叠加的示意图如图所示，图中实线表示处于波峰的各质点，虚线表示处于波谷的各质点。图中a、b、c三点中，振动情况加强的质点有　　　　 ，振动情况减弱的质点有　　 。

解析:在两列波叠加的区域内，图中a点是实线与实线的交点，表明两列波都要求a点为正向位移，a点的位移是两列波位移的矢量之和，即振幅之和，是振动情况加强的质点。同样处于虚线与虚线交点的b质点，也是振动情况加强的点。只是b是处于反向最大位移(也等于两列波振幅之和)。因此处于实线与虚线交点的质点c是振动情况减弱的质点，其此刻位移为零。

本题叠加的两列波是波长(频率)相同的两列波，满足干涉的条件。过半个周期，图中实线变为虚线，虚线变为实线。a、b仍是振动情况加强的点，c点仍是振动情况减弱的点。即a、b以两列波振幅的和为振幅振动，C点则以它们振幅之差为振幅振动，且加强点与减弱点间隔排列。

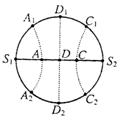[例6]如图所示，在同一均匀媒质中有S₁、S₂两个波源，这个波源的频率、振动方向均相同，且振动的步调完全一致，S₁、S₂之间相距两个波长，D点为S₁、S₂连线中点，今以D点为圆心，以R=DS₁为半径画圆，问在该圆周上(S₁、S₂两波源除外)共有几个加强点？

分析：干涉强、弱区的判断方法有两种：

(1)在波峰与波峰相遇或波谷与波谷相遇处是干涉加强区；在波峰与波谷相遇或波谷与波峰相遇处是干涉减弱区。

(2)与相同波源的距离差为半波长的偶数倍处是干涉加强区；与相同波源的距离差为半波长的奇数倍处是干涉减弱区。

解答：由干涉强、弱的第二种判断方法可知，干涉加强区的集合实际上是以两波源所在处为焦点的双曲线簇。由此不难判断：以波源边线为直径的贺周上分布看，到两波源距离差等于0的两个加强是D₁、D₂；到两波源距离差等于的四个加强是A₁、A₂、C₁、C₂。即：除两波源外，圆周上振动加强是共有六个。

[例7]如图所示，在半径为R=45m的圆心O和圆周A处，有两个功率差不多的喇叭，同时发出两列完全相同的声波，且波长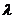=10m。若人站在B处，正好听不到声音；若逆时针方向从B走到A，则时而听到时而听不到声音。试问在到达A点之前，还有几处听不到声音？　　　　　　　　　　　　　　　　　　　　　　　　　　　　

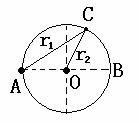解析：因为波源A、O到B点的波程差为Δr=r₁-r₂=R=45m=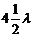，所以B点发生干涉相消现象。

在圆周任一点C上听不到声音的条件为：

Δr = r₁-r₂ =±(2k+1)λ/2=±5(2k+1)

将r₂=R=45m代入上式得：r₁=±5(2k+1)+ r₂

所以：r₁=10k+50　 或　 r₁= -10k+40

而0 < r₁ < 90m，所以有：0 <(10k+50) < 90m 和　 0 <(-10k+40) < 90m

求得 :-5 < k < 4

即k = -4、-3、-2、-1、0、1、2、3，所以在到达A点之前有八处听不到声音。

3.波的衍射:波可以绕过障碍物继续传播的现象．

衍射是波的特性，一切波都能发生衍射．

产生明显衍射现象的条件是：障碍物或孔的尺寸比波长小或与波长相差不多。

例如：声波的波长一般比院坡大，“隔堵有耳”就是声波衍射的例证．

说明：衍射是波特有的现象．