
2.(2008·江苏高考)2007年度诺贝尔物理学奖授予了法国和德国的两位科学家,以表彰他们发现“巨磁电阻效应”.基于巨磁电阻效应开发的用于读取硬盘数据的技术,被认为是纳米技术的第一次真正应用.在下列有关其他电阻应用的说法中,错误的是 ( )
A.热敏电阻可应用于温度测控装置中
B.光敏电阻是一种光电传感器
C.电阻丝可应用于电热设备中
D.电阻在电路中主要起到通过直流、阻碍交流的作用
解析:热敏电阻对温度很敏感,光敏电阻对光照很敏感,电阻丝可用于电加热,这很常见,所以A、B、C三个说法均正确;交流电、直流电均可通过电阻,电阻对它们均可产生阻碍作用,所以D错误.
 答案:D
答案:D
1.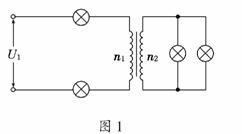 如图1所示,电路中有四个完全相同的灯泡,额定电压均为U,额定功率均为P,变压器为理想变压器,现在四个灯泡都正常发光,则变压器的匝数比n1∶n2和电源电压U1分别为
( )
如图1所示,电路中有四个完全相同的灯泡,额定电压均为U,额定功率均为P,变压器为理想变压器,现在四个灯泡都正常发光,则变压器的匝数比n1∶n2和电源电压U1分别为
( )
A.1∶2 2U B.1∶2 4U
C.2∶1 4U D.2∶1 2U
解析:设灯泡正常发光时,额定电流为I0.由题图可知,原线圈中电流I原=I0,副线圈中两灯并联,副线圈中电流I副=2I0,U副=U,根据理想变压器的基本规律:I原n1=I副n2得n1∶n2=2∶1;U原/U副=n1/n2得U原=2U,所以U1=4U.C项正确.
答案:C
12.已知点P(-3,0),点A在y轴上,点Q在x轴非负半轴上,点M在直线AQ上,满足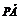 ·
·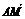 =0,
=0,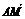 =-
=-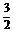
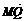 .
.
(1)当点A在y轴上移动时,求动点M的轨迹C的方程;
(2)设轨迹C的准线为l,焦点为F,过F作直线m交轨迹C于G,H两点,过点G作平行于轨迹C的对称轴的直线n,且n∩l=E,试问点E,O,H(O为坐标原点)是否在同一条直线上?并说明理由.
解 (1)设M(x,y)为轨迹上任意一点,
A(0,b),Q(a,0)(a≥0),
则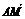 =(x,y-b),
=(x,y-b),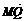 =(a-x,-y),
=(a-x,-y),
∵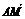 =-
=-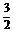
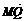 ,
,
∴(x,y-b)=-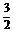 (a-x,-y),
(a-x,-y),
∴ ,从而
,从而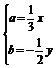 .
.
∴A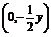 ,且
,且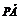 =
=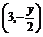 ,
, 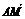 =
=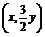 .
.
∵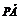 ·
·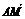 =0,
=0,
∴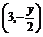 ·
·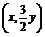 =0,即3x-
=0,即3x-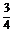 y2=0,
y2=0,
∴y2=4x,故M点的轨迹方程为y2=4x.
(2)轨迹C的焦点为F(1,0),准线为l:x=-1,对称轴为x轴.设直线m的方程为y=k(x-1)(k≠0),
由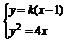
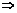 ky2-4y-4k=0,
ky2-4y-4k=0,
设G(x1,y1),H(x2,y2),
则由根与系数的关系得,y1y2=-4,
又由已知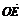 =(-1,y1),
=(-1,y1), =
=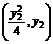 ,
,
∴(-1)×y2-y1×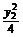 =-y2-
=-y2-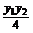 ·y2=-y2+y2=0,
·y2=-y2+y2=0,
∴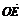 ∥
∥ ,故O,E,H三点共线.
,故O,E,H三点共线.
11.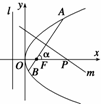 如图所示,倾斜角为
如图所示,倾斜角为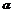 的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
(1)求抛物线焦点F的坐标及准线l的方程;
(2)若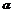 为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2
为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2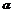 为定值,
为定值,
并求此定值.
(1)解 由已知得2 p=8,∴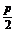 =2,
=2,
∴抛物线的焦点坐标为F(2,0),准线方程为x=-2.
(2)证明 设A(xA,yA),B(xB,yB),直线AB的斜率为k=tan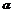 ,则直线方程为y=k(x-2),
,则直线方程为y=k(x-2),
将此式代入y2=8x,得k2x2-4(k2+2)x+4k2=0,
故xA+xB=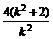 ,
,
记直线m与AB的交点为E(xE,yE),则
xE=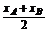 =
=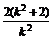 ,yE=k(xE-2)=
,yE=k(xE-2)=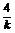 ,
,
故直线m的方程为y-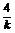 =-
=-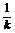
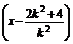 ,
,
令y=0,得点P的横坐标xP=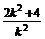 +4,
+4,
故|FP|=xP-2=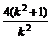 =
=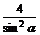 ,
,
∴|FP|-|FP|cos2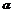 =
=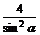 (1-cos2
(1-cos2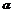 )=
)=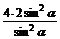 =8,为定值.
=8,为定值.
10.抛物线顶点在原点,它的准线过双曲线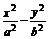 =1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知抛物线与双曲线的一个交点为
=1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知抛物线与双曲线的一个交点为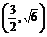 ,求抛物线与双曲线方程.
,求抛物线与双曲线方程.
解 由题设知,抛物线以双曲线的右焦点为焦点,准线过双曲线的左焦点,∴p=2c.抛物线方程为y2=4cx.
∵抛物线过点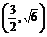 ,∴6=4c·
,∴6=4c·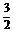 .
.
∴c=1,故抛物线方程为y2=4x.
又双曲线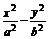 =1过点
=1过点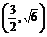 ,
,
∴ =1.又a2+b2=c2=1.
=1.又a2+b2=c2=1.
∴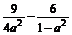 =1.∴a2=
=1.∴a2=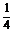 或a2=9(舍).
或a2=9(舍).
∴b2=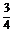 ,故双曲线方程为4x2-
,故双曲线方程为4x2-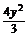 =1.
=1.
9.已知抛物线y2=2px(p>0)有一个内接直角三角形,直角顶点在原点,斜边长为2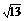 ,一直角边的方程是y=2x,求抛物线的方程.
,一直角边的方程是y=2x,求抛物线的方程.
解 因为一直角边的方程是y=2x,
所以另一直角边的方程是y=- x.
x.
由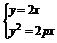 ,解得
,解得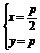 ,或
,或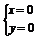 (舍去),
(舍去),
由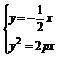 ,解得
,解得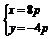 ,或
,或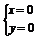 (舍去),
(舍去),
∴三角形的另两个顶点为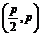 和(8 p,-4p).
和(8 p,-4p).
∴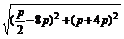 =2
=2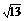 .
.
解得p=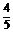 ,故所求抛物线的方程为y2=
,故所求抛物线的方程为y2=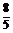 x.
x.
8.(2008·江西理,15)过抛物线x2=2py(p>0)的焦点F作倾斜角为30°的直线,与抛物线分别交于A、B两点(点A在y轴左侧),则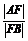 =
.
=
.
答案 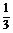
7.(2008·全国Ⅱ理,15)已知F为抛物线C:y2=4x的焦点,过F且斜率为1的直线交抛物线C于A、B两点.设|FA|>|FB|,则|FA|与|FB|的比值等于 .
答案 3+2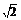
6.设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点.若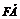 +
+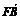 +
+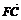 =0,则|
=0,则|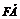 |+|
|+|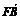 |+|
|+|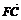 |=
.
|=
.
答案 6
5.设坐标原点为O,抛物线y2=2x与过焦点的直线交于A、B两点,则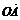 ·
·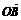 =
.
=
.
答案 -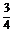
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com