
解:(1)N Z, N
Z, N Q, R
Q, R Z, R
Z, R Q, Φ
Q, Φ {0}
{0}
(2)∵A={x∈R|x -3x-4=0}={-1,4},
-3x-4=0}={-1,4},
B={x∈Z||x|<10}={-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9}
∴A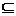 B正确
B正确
(3)对任意一个集合A,都有A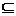 A,
A,
(4)集合{a,b}的子集有:Φ、{a}、{b}、{a,b}
(5)A、B的关系为 .
.
例3 解不等式x+3<2,并把结果用集合表示出来.
解:{x∈R|x+3<2}={x∈R|x<-1}.
例1(1)
写出N,Z,Q,R的包含关系,并用文氏图表示
(2) 判断下列写法是否正确
①Φ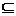 A ②Φ
A ②Φ A ③
A ③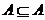 ④A
④A A
A
解(1):N Z
Z Q
Q R
R
(2)①正确;②错误,因为A可能是空集
③正确;④错误
例2 (1)填空:N___Z, N___Q, R___Z, R___Q,
Φ___{0}
(2)若A={x∈R|x -3x-4=0},B={x∈Z||x|<10},则A
-3x-4=0},B={x∈Z||x|<10},则A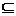 B正确吗?
B正确吗?
(3)是否对任意一个集合A,都有A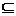 A,为什么?
A,为什么?
(4)集合{a,b}的子集有那些?
(一) 子集
1 定义:
(1)子集:一般地,对于两个集合A与B,如果集合A的任何一
个元素都是集合B的元素,我们就说集合A包含于集
合B,或集合B包含集合A
记作: ,A
,A B或B
B或B A
A
读作:A包含于B或B包含A

当集合A不包含于集合B,或集合B不包含集合A时,则记
作A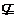 B或B
B或B A
A
注: 有两种可能
有两种可能
(1)A是B的一部分,;(2)A与B是同一集合
(2)集合相等:一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,记作A=B
(3)真子集:对于两个集合A与B,如果 ,并且
,并且 ,我们就说集合A是集合B的真子集,记作:A
,我们就说集合A是集合B的真子集,记作:A B或B
B或B A, 读作A真包含于B或B真包含A
A, 读作A真包含于B或B真包含A
(4)子集与真子集符号的方向

(5)空集是任何集合的子集 Φ
Φ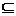 A
A
空集是任何非空集合的真子集 Φ
Φ A 若A≠Φ,则Φ
A 若A≠Φ,则Φ A
A
任何一个集合是它本身的子集
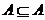
(6)易混符号
①“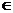 ”与“
”与“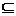 ”:元素与集合之间是属于关系;集合与集合之间是包含关系
”:元素与集合之间是属于关系;集合与集合之间是包含关系 如
如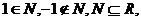 Φ
Φ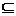 R,{1}
R,{1}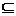 {1,2,3}
{1,2,3}
②{0}与Φ:{0}是含有一个元素0的集合,Φ是不含任何元素的集合
 如 Φ
如 Φ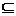 {0}
{0} 不能写成Φ={0},Φ∈{0}
不能写成Φ={0},Φ∈{0}
(1)回答概念:集合、元素、有限集、无限集、空集、列举法、描述法、文氏图
(2)用列举法表示下列集合:
① {-1,1,2}
{-1,1,2}
②数字和为5的两位数} {14,23,32,41,50}
(3)用描述法表示集合:

(4)集合中元素的特性是什么?
(5)用列举法和描述法分别表示:“与2相差3的所有整数所组成的
集合” {-1,5}
{-1,5}
问题:观察下列两组集合,说出集合A与集合B的关系(共性)
(1)A={1,2,3},B={1,2,3,4,5}
(2)A=N,B=Q
(3)A={-2,4},
(集合A中的任何一个元素都是集合B的元素)
10.补写出下列名句名篇中的空缺部分。
(1)惟草木之零落兮,____。(屈原《离骚》)
(2)君子博学而日参省乎己,____。(荀子《劝学》)
(3)桃李不言,____。(司马迁《史记·李将军列传》)
(4)同是天涯沦落人 ,____。(白居易《琵琶行》)
(5)胭脂泪 ,相留醉,几时重?!(李煜 《乌夜啼》)
(6)哀吾生之须臾,____。(苏轼《赤壁赋》)
(7)月,常常寄寓人们的相思之情。柳永 《雨霖铃 》“今宵酒醒何处?杨柳岸、晓风残月”抒发了与爱人别离后内心的凄凉之情;张九龄 《望月怀远 》“ ,”则叩动了天涯儿女的共同心弦,经久不息地响彻在中华大地。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com