
54.两向量的夹角公式
 (a=
(a= ,b=
,b=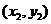 ).
).
53.平面向量的坐标运算
(1)设a= ,b=
,b=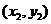 ,则a+b=
,则a+b= .
.
(2)设a= ,b=
,b=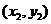 ,则a-b=
,则a-b= .
.
(3)设A ,B
,B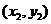 ,则
,则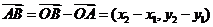 .
.
(4)设a= ,则
,则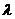 a=
a=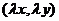 .
.
(5)设a= ,b=
,b=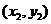 ,则a·b=
,则a·b= .
.
52.a·b的几何意义
数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积.
51.a与b的数量积(或内积)
a·b=|a||b|cosθ.
50.向量平行的坐标表示
设a= ,b=
,b=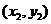 ,且b
,且b 0,则a
0,则a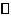 b(b
b(b 0)
0) .
.
49.平面向量基本定理
如果e1、e 2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数λ1、λ2,使得a=λ1e1+λ2e2.
不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底.
48.向量的数量积的运算律
(1) a·b= b·a (交换律);(2)(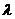 a)·b=
a)·b= 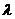 (a·b)=
(a·b)=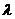 a·b= a·(
a·b= a·(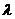 b);
b);
(3)(a+b)·c= a ·c +b·c.
47.实数与向量的积的运算律
设λ、μ为实数,那么
(1) 结合律:λ(μa)=(λμ)a;
(2)第一分配律:(λ+μ)a=λa+μa;(3)第二分配律:λ(a+b)=λa+λb.
46.角的变形:
向量
45.最简单的三角不等式及其解集
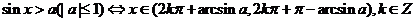 .
.
 .
.
 .
.
 .
.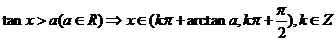 .
.
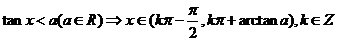 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com