
6.对称轴与对称中心:
 的对称轴为
的对称轴为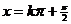 ,对称中心为
,对称中心为 ;
;
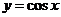 的对称轴为
的对称轴为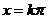 ,对称中心为
,对称中心为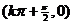 ;
;
对于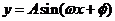 和
和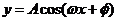 来说,对称中心与零点相联系,对称轴与最值点联系。
来说,对称中心与零点相联系,对称轴与最值点联系。
5.由y=Asin(ωx+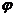 )的图象求其函数式:
)的图象求其函数式:
给出图象确定解析式y=Asin(ωx+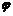 )的题型,有时从寻找“五点”中的第一零点(-
)的题型,有时从寻找“五点”中的第一零点(- ,0)作为突破口,要从图象的升降情况找准第一个零点的位置。
,0)作为突破口,要从图象的升降情况找准第一个零点的位置。
4.由y=sinx的图象变换出y=sin(ωx+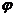 )的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现 无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
无论哪种变形,请切记每一个变换总是对字母x而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换)
先将y=sinx的图象向左(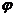 >0)或向右(
>0)或向右(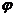 <0=平移|
<0=平移|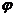 |个单位,再将图象上各点的横坐标变为原来的
|个单位,再将图象上各点的横坐标变为原来的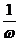 倍(ω>0),便得y=sin(ωx+
倍(ω>0),便得y=sin(ωx+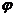 )的图象。
)的图象。
途径二:先周期变换(伸缩变换)再平移变换。
先将y=sinx的图象上各点的横坐标变为原来的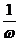 倍(ω>0),再沿x轴向左(
倍(ω>0),再沿x轴向左(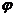 >0)或向右(
>0)或向右(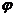 <0=平移
<0=平移 个单位,便得y=sin(ωx+
个单位,便得y=sin(ωx+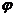 )的图象。
)的图象。
3.函数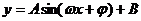
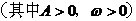
最大值是 ,最小值是
,最小值是 ,周期是
,周期是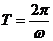 ,频率是
,频率是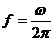 ,相位是
,相位是 ,初相是
,初相是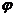 ;其图象的对称轴是直线
;其图象的对称轴是直线 ,凡是该图象与直线
,凡是该图象与直线 的交点都是该图象的对称中心。
的交点都是该图象的对称中心。
2.三角函数的单调区间:
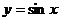 的递增区间是
的递增区间是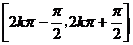
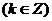 ,
,
递减区间是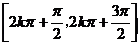
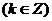 ;
;
 的递增区间是
的递增区间是
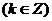 ,
,
递减区间是
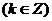 ,
,
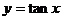 的递增区间是
的递增区间是
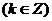 ,
,
1.正弦函数、余弦函数、正切函数的图像

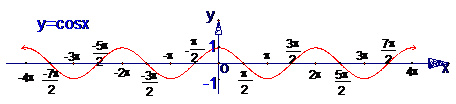

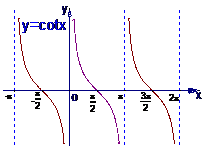
2.热点问题是三角函数的图象和性质,特别是y=Asin(wx+φ)的图象及其变换;
近几年高考降低了对三角变换的考查要求,而加强了对三角函数的图象与性质的考查,因为函数的性质是研究函数的一个重要内容,是学习高等数学和应用技术学科的基础,又是解决生产实际问题的工具,因此三角函数的性质是本章复习的重点。在复习时要充分运用数形结合的思想,把图象与性质结合起来,即利用图象的直观性得出函数的性质,或由单位圆上线段表示的三角函数值来获得函数的性质,同时也要能利用函数的性质来描绘函数的图象,这样既有利于掌握函数的图象与性质,又能熟练地运用数形结合的思想方法。
预测07年高考对本讲内容的考察为:
1.题型为1道选择题(求值或图象变换),1道解答题(求值或图像变换);
3.结合具体实例,了解y=Asin(wx+φ)的实际意义;能借助计算器或计算机画出y=Asin(wx+φ)的图像,观察参数A,w,φ对函数图像变化的影响。
2.借助图像理解正弦函数、余弦函数在[0,2π],正切函数在(-π/2,π/2)上的性质(如单调性、最大和最小值、图像与x轴交点等);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com