5．三角等式的证明

(1)三角恒等式的证题思路是根据等式两端的特征，通过三角恒等变换，应用化繁为简、左右同一等方法，使等式两端化“异”为“同”；

(2)三角条件等式的证题思路是通过观察，发现已知条件和待证等式间的关系，采用代入法、消参法或分析法进行证明。

4．三角函数的求值类型有三类

(1)给角求值：一般所给出的角都是非特殊角，要观察所给角与特殊角间的关系，利用三角变换消去非特殊角，转化为求特殊角的三角函数值问题；

(2)给值求值：给出某些角的三角函数式的值，求另外一些角的三角函数值，解题的关键在于“变角”，如等，把所求角用含已知角的式子表示，求解时要注意角的范围的讨论；

(3)给值求角：实质上转化为“给值求值”问题，由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。

3．三角函数式的化简

常用方法：①直接应用公式进行降次、消项；②切割化弦，异名化同名，异角化同角；③ 三角公式的逆用等。(2)化简要求：①能求出值的应求出值；②使三角函数种数尽量少；③使项数尽量少；④尽量使分母不含三角函数；⑤尽量使被开方数不含三角函数。

(1)降幂公式

；；。

(2)辅助角公式

，

。

2．二倍角公式

；

；

。

1．两角和与差的三角函数

；

；

。

从近几年的高考考察的方向来看，这部分的高考题以选择、解答题出现的机会较多，有时候也以填空题的形式出现，它们经常与三角函数的性质、解三角形及向量联合考察，主要题型有三角函数求值，通过三角式的变换研究三角函数的性质。

本讲内容是高考复习的重点之一，三角函数的化简、求值及三角恒等式的证明是三角变换的基本问题。历年高考中，在考察三角公式的掌握和运用的同时，还注重考察思维的灵活性和发散性，以及观察能力、运算及观察能力、运算推理能力和综合分析能力。

3．能运用上述公式进行简单的恒等变换(包括引导导出积化和差、和差化积、半角公式，但不要求记忆)。

2．能从两角差的余弦公式导出两角和与差的正弦、余弦、正切公式，二倍角的正弦、余弦、正切公式，了解它们的内在联系；

1．经历用向量的数量积推导出两角差的余弦公式的过程，进一步体会向量方法的作用；

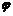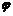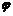7．判断y=－Asin(ωx+)(ω＞0)的单调区间，只需求y=Asin(ωx+)的相反区间即可，一般常用数形结合而求y=Asin(－ωx+)(－ω＜0＝单调区间时，则需要先将x的系数变为正的，再设法求之。