
4.等比数列前n项和公式
一般地,设等比数列 的前n项和是
的前n项和是
 ,当
,当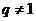 时,
时, 或
或 ;当q=1时,
;当q=1时, (错位相减法)。
(错位相减法)。
说明:(1) 和
和 各已知三个可求第四个;(2)注意求和公式中是
各已知三个可求第四个;(2)注意求和公式中是 ,通项公式中是
,通项公式中是 不要混淆;(3)应用求和公式时
不要混淆;(3)应用求和公式时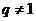 ,必要时应讨论
,必要时应讨论 的情况。
的情况。
3.等比中项
如果在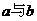 中间插入一个数
中间插入一个数 ,使
,使 成等比数列,那么
成等比数列,那么 叫做
叫做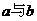 的等比中项(两个符号相同的非零实数,都有两个等比中项)。
的等比中项(两个符号相同的非零实数,都有两个等比中项)。
2.等比数列通项公式为: 。
。
说明:(1)由等比数列的通项公式可以知道:当公比 时该数列既是等比数列也是等差数列;(2)等比数列的通项公式知:若
时该数列既是等比数列也是等差数列;(2)等比数列的通项公式知:若 为等比数列,则
为等比数列,则 。
。
1.等比数列定义
一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比;公比通常用字母 表示
表示 ,即:
,即: :
: 数列对于数列(1)(2)(3)都是等比数列,它们的公比依次是2,5,
数列对于数列(1)(2)(3)都是等比数列,它们的公比依次是2,5, 。(注意:“从第二项起”、“常数”
。(注意:“从第二项起”、“常数” 、等比数列的公比和项都不为零)
、等比数列的公比和项都不为零)
等比数列与等差数列同样在高考中占有重要的地位,是高考出题的重点。客观性的试题考察等比数列的概念、性质、通项公式、求和公式等基础知识和基本性质的灵活应用,对基本的运算要求比较高,解答题大多以数列知识为工具。
预测07年高考对本讲的考察为:
(1)题型以等比数列的公式、性质的灵活应用为主的1~2道客观题目;
(2)关于等比数列的实际应用问题或知识交汇题的解答题也是重点;
(3)解决问题时注意数学思想的应用,象通过逆推思想、函数与方程、归纳猜想、等价转化、分类讨论等,它将能灵活考察考生运用数学知识分析问题和解决问题的能力。
3.能在具体的问题情境中,发现数列的等比关系,并能用有关知识解决相应的问题。体会等比数列与指数函数的关系。
2.探索并掌握等差数列的通项公式与前n项和的公式;
1.通过实例,理解等比数列的概念;
6.(1) ,
,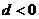 时,
时, 有最大值;
有最大值; ,
, 时,
时, 有最小值;(2)
有最小值;(2) 最值的求法:①若已知
最值的求法:①若已知 ,可用二次函数最值的求法(
,可用二次函数最值的求法(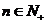 );②若已知
);②若已知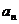 ,则
,则 最值时
最值时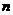 的值(
的值(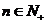 )可如下确定
)可如下确定 或
或 。
。
5.说明:设数列 是等差数列,且公差为
是等差数列,且公差为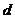 ,(Ⅰ)若项数为偶数,设共有
,(Ⅰ)若项数为偶数,设共有 项,则①
项,则① 奇
奇
 偶
偶 ; ②
; ②  ;(Ⅱ)若项数为奇数,设共有
;(Ⅱ)若项数为奇数,设共有 项,则①
项,则① 偶
偶
 奇
奇 ;②
;② 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com