2．基本不等式：(a,b≥0)

①探索并了解基本不等式的证明过程；

②会用基本不等式解决简单的最大(小)问题。

1．不等关系

通过具体情境，感受在现实世界和日常生活中存在着大量的不等关系，了解不等式(组)的实际背景；

3．数学思想

(1)迭加累加(等差数列的通项公式的推导方法)若，则……；

(2)迭乘累乘(等比数列的通项公式的推导方法)若，则……；

(3)逆序相加(等差数列求和公式的推导方法)；

(4)错位相减(等比数列求和公式的推导方法)。

2．常用结论

(1)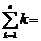 1+2+3+...+n =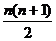 　　　

(2)1+3+5+...+(2n-1) =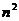

　 (3)　

(4)　

(5)　

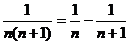
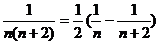
(6)

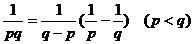
1．数列求和的常用方法

(1)公式法：适用于等差、等比数列或可转化为等差、等比数列的数列；

(2)裂项相消法：适用于其中{ 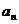}是各项不为0的等差数列，c为常数；部分无理数列、含阶乘的数列等；

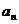(3)错位相减法：适用于其中{ }是等差数列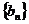，是各项不为0的等比数列。

(4)倒序相加法：类似于等差数列前n项和公式的推导方法.

(5)分组求和法

(6)累加(乘)法等。

2．递归数列

数列的连续若干项满足的等量关系a_n+k=f(a_n+k－1,a_n+k－2,…,a_n)称为数列的递归关系。由递归关系及k个初始值可以确定的一个数列叫做递归数列。如由a_n+1=2a_n+1，及a₁=1，确定的数列即为递归数列。

递归数列的通项的求法一般说来有以下几种：

(1)归纳、猜想、数学归纳法证明。

(2)迭代法。

(3)代换法。包括代数代换，对数代数，三角代数。

(4)作新数列法。最常见的是作成等差数列或等比数列来解决问题。

1．数列求通项与和

(1)数列前n项和S_n与通项a_n的关系式：a_n=　 。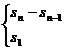

(2)求通项常用方法

①作新数列法。作等差数列与等比数列；

②累差叠加法。最基本的形式是：a_n=(a_n－a_n－1)+(a_n－1+a_n－2)+…+(a₂－a₁)+a₁；

③归纳、猜想法。

(3)数列前n项和

①重要公式：1+2+…+n=n(n+1)；

1²+2²+…+n²=n(n+1)(2n+1)；

1³+2³+…+n³=(1+2+…+n)²=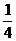n²(n+1)²；

②等差数列中，S_m+n=S_m+S_n+mnd；

③等比数列中，S_m+n=S_n+qⁿS_m=S_m+q^mS_n；

④裂项求和

将数列的通项分成两个式子的代数和，即a_n=f(n+1)－f(n)，然后累加抵消掉中间的许多项，这种先裂后消的求和法叫裂项求和法。用裂项法求和，需要掌握一些常见的裂项，如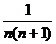：、=－、n·n！=(n+1)!－n!、C_n－1^r－1=C_n^r－C_n－1^r、=－等。

⑤错项相消法

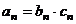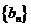对一个由等差数列及等比数列对应项之积组成的数列的前n项和，常用错项相消法。, 其中是等差数列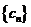， 是等比数列，记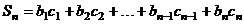，则，…

⑥并项求和

把数列的某些项放在一起先求和，然后再求S_n。

数列求通项及和的方法多种多样，要视具体情形选用合适方法。

⑦通项分解法：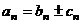

2．也可能为一道知识交汇题是数列与函数、不等式、解析几何、应用问题上等联系的综合题，以及数列、数学归纳法等有机结合。

1．可能为一道考察关于数列的推导能力或解决生产、生活中的实际问题的解答题；