
1.不等关系
通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景;
3.几个重要不等式
(1)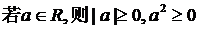
(2)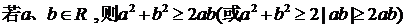 (当仅当a=b时取等号)
(当仅当a=b时取等号)
(3)如果a,b都是正数,那么 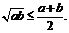 (当仅当a=b时取等号)
(当仅当a=b时取等号)
最值定理:若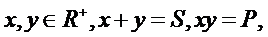 则:
则:
1如果P是定值, 那么当x=y时,S的值最小;2如果S是定值, 那么当x=y时,P的值最大;
注意:1前提:“一正、二定、三相等”,如果没有满足前提,则应根据题目创设情境;还要注意选择恰当的公式;2“和定 积最大,积定 和最小”,可用来求最值;3均值不等式具有放缩功能,如果有多处用到,请注意每处取等的条件是否一致。
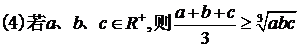 (当仅当a=b=c时取等号);
(当仅当a=b=c时取等号);
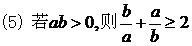 (当仅当a=b时取等号)。
(当仅当a=b时取等号)。
2.不等式证明还有一些常用的方法:换元法、放缩法、反证法、函数单调性法、判别式法、数形结合法等。换元法主要有三角代换,均值代换两种,在应用换元法时,要注意代换的等价性。放缩性是不等式证明中最重要的变形方法之一,放缩要有的放矢,目标可以从要证的结论中考查。有些不等式,从正面证如果不易说清楚,可以考虑反证法 凡是含有“至少”、“惟一”或含有其他否定词的命题,适宜用反证法。
凡是含有“至少”、“惟一”或含有其他否定词的命题,适宜用反证法。
证明不等式时,要依据题设、题目的特点和内在联系,选择适当的证明方法,要熟悉各种证法中的推理思维,并掌握相应的步骤、技巧和语言特点。
1.不等式证明常用的方法有:比较法、综合法和分析法,它们是证明不等式的最基本的方法。
(1)比较法证不等式有作差(商)、变形、判断三个步骤,变形的主要方向是因式分解、配方,判断过程必须详细叙述:如果作差以后的式子可以整理为关于某一个变量的二次式,则考虑用判别式法证;
(2)综合法是由因导果,而分析法是执果索因,两法相互转换,互相渗透,互为前提,充分运用这一辩证关系,可以增加解题思路,开扩视野。
3.常用的证明不等式的方法
(1)比较法
比较法证明不等式的一般步骤:作差-变形-判断-结论;为了判断作差后的符号,有时要把这个差变形为一个常数,或者变形为一个常数与一个或几个平方和的形式,也可变形为几个因式的积的形式,以便判断其正负。
(2)综合法
利用某些已经证明过的不等式(例如算术平均数与几何平均数的定理)和不等式的性质,推导出所要证明的不等式,这个证明方法叫综合法;利用某些已经证明过的不等式和不等式的性质时要注意它们各自成立的条件。
综合法证明不等式的逻辑关系是: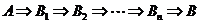 ,及从已知条件
,及从已知条件 出发,逐步推演不等式成立的必要条件,推导出所要证明的结论
出发,逐步推演不等式成立的必要条件,推导出所要证明的结论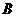 。
。
(3)分析法
证明不等式时,有时可以从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题,如果能够肯定这些充分条件都已具备,那么就可以断定原不等式成立,这种方法通常叫做分析法。
(1)“分析法”是从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题,即“执果索因”;
(2)综合过程有时正好是分析过程的逆推,所以常用分析法探索证明的途径,然后用综合法的形式写出证明过程。
2.基本不等式
定理1:如果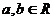 ,那么
,那么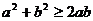 (当且仅当
(当且仅当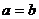 时取“
时取“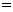 ”)。
”)。
说明:(1)指出定理适用范围: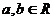 ;(2)强调取“
;(2)强调取“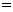 ”的条件
”的条件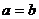 。
。
定理2:如果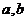 是正数,那么
是正数,那么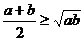 (当且仅当
(当且仅当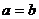 时取“=”)
时取“=”)
说明:(1)这个定理适用的范围: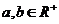 ;(2)我们称
;(2)我们称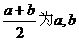 的算术平均数,称
的算术平均数,称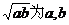 的几何平均数。即:两个正数的算术平均数不小于它们的几何平均数。
的几何平均数。即:两个正数的算术平均数不小于它们的几何平均数。
1.不等式的性质
比较两实数大小的方法--求差比较法
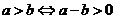 ;
;
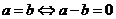 ;
;
 。
。
定理1:若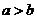 ,则
,则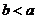 ;若
;若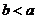 ,则
,则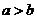 .即
.即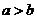
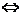
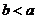 。
。
说明:把不等式的左边和右边交换,所得不等式与原不等式异向,称为不等式的对称性。
定理2:若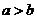 ,且
,且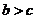 ,则
,则 。
。
说明:此定理证明的主要依据是实数运算的符号法则及两正数之和仍是正数;定理2称不等式的传递性。
定理3:若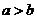 ,则
,则 。
。
说明:(1)不等式的两边都加上同一个实数,所得不等式与原不等式同向;
(2)定理3的证明相当于比较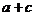 与
与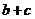 的大小,采用的是求差比较法;
的大小,采用的是求差比较法;
(3)定理3的逆命题也成立;
(4)不等式中任何一项改变符号后,可以把它从一边移到另一边。
定理3推论:若 。
。
说明:(1)推论的证明连续两次运用定理3然后由定理2证出;(2)这一推论可以推广到任意有限个同向不等式两边分别相加,即:两个或者更多个同向不等式两边分别相加,所得不等式与原不等式同向;(3)同向不等式:两个不等号方向相同的不等式;异向不等式:两个不等号方向相反的不等式。
定理4.如果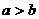 且
且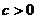 ,那么
,那么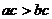 ;如果
;如果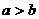 且
且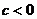 ,那么
,那么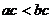 。
。
推论1:如果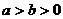 且
且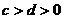 ,那么
,那么 。
。
说明:(1)不等式两端乘以同一个正数,不等号方向不变;乘以同一个负数,不等号方向改变;(2)两边都是正数的同向不等式的两边分别相乘,所得不等式与原不等式同向;(3)推论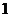 可以推广到任意有限个两边都是正数的同向不等式两边分别相乘。这就是说,两个或者更多个两边都是正数的同向不等式两边分别相乘,所得不等式与原不等式同向。
可以推广到任意有限个两边都是正数的同向不等式两边分别相乘。这就是说,两个或者更多个两边都是正数的同向不等式两边分别相乘,所得不等式与原不等式同向。
推论2:如果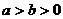 , 那么
, 那么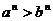
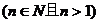 。
。
定理5:如果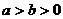 ,那么
,那么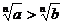
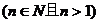 。
。
2.利用基本不等式解决像函数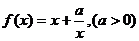 的单调性或解决有关最值问题是考察的重点和热点,应加强训练。
的单调性或解决有关最值问题是考察的重点和热点,应加强训练。
不等式历来是高考的重点内容。对于本将来讲,考察有关不等式性质的基础知识、基本方法,而且还考察逻辑推理能力、分析问题、解决问题的能力。本将内容在复习时,要在思想方法上下功夫。
预测2007年的高考命题趋势:
1.从题型上来看,选择题、填空题都有可能考察,把不等式的性质与函数、三角结合起来综合考察不等式的性质、函数单调性等,多以选择题的形式出现,解答题以含参数的不等式的证明、求解为主;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com