
1.(★★★)飞机在飞行时受到的空气阻力与速率的平方成正比,若飞机以速率v匀速飞行时,发动机的功率为P,则当飞机以速率n v匀速飞行时,发动机的功率为
A.np B.2np C.n2p D.n3p
2.(★★★★)汽车在水平公路上行驶,车受的阻力为车重的0.01倍,当速度为4 m/s时,加速度为0.4 m/s2.若保持此时的功率不变继续行驶,汽车能达到的最大速度是________m/s. (g取10 m/s2)
●案例探究
[例1](★★★★)汽车发动机额定功率为60 kW,汽车质量为5.0×103 kg,汽车在水平路面行驶时,受到的阻力大小是车重的0.1倍,试求:
(1)汽车保持额定功率从静止出发后能达到的最大速度是多少?
(2)若汽车从静止开始,以0.5 m/s2的加速度匀加速运动,则这一加速度能维持多长时间?
命题意图:考查对汽车起动的两类问题及过程的分析能力.B级要求.
错解分析:(1)对v、F、a、p间相互制约关系分析不透,挖掘不到临界条件和临界状态,(2)在第(2)问中认为功率刚达到最大(即额定功率)时,速度亦达到了最大.
解题方法与技巧:(1)汽车以恒定功率起动时,它的牵引力F将随速度v的变化而变化,其加速度a也随之变化,具体变化过程可采用如下示意图表示:

由此可得汽车速度达到最大时,a=0,
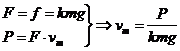 =12 m/s
=12 m/s
 (2)要维持汽车加速度不变,就要维持其牵引力不变,汽车功率将随v增大而增大,当P达到额定功率P额后,不能再增加,即汽车就不可能再保持匀加速运动了.具体变化过程可用如下示意图表示:
(2)要维持汽车加速度不变,就要维持其牵引力不变,汽车功率将随v增大而增大,当P达到额定功率P额后,不能再增加,即汽车就不可能再保持匀加速运动了.具体变化过程可用如下示意图表示:
所以,汽车达到最大速度之前已经历了两个过程:匀加速和变加速,匀加速过程能维持到汽车功率增加到P额的时刻,设匀加速能达到最大速度为v,则此时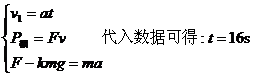
[例2](★★★★★)电动机通过一绳子吊起质量为8 kg的物体,绳的拉力不能超过120 N,电动机的功率不能超过1200 W,要将此物体由静止起用最快的方式吊高90 m(已知此物体在被吊高接近90 m时,已开始以最大速度匀速上升)所需时间为多少?
命题意图:考查对机械启动两类问题的理解及迁移应用的创新能力.B级要求.错解分析:对第二过程分析不透,加之思维定势,无法巧妙地借助动能定理求t2.
解题方法与技巧:
此题可以用机车起动类问题的思路,即将物体吊高分为两个过程处理:第一过程是以绳所能承受的最大拉力拉物体,使物体匀加速上升,第一个过程结束时,电动机刚达到最大功率.第二个过程是电动机一直以最大功率拉物体,拉力逐渐减小,当拉力等于重力时,物体开始匀速上升.
在匀加速运动过程中加速度为
a= m/s2=5 m/s2
m/s2=5 m/s2
末速度vt= =10 m/s
=10 m/s
上升的时间t1=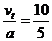 s=2 s
s=2 s
上升高度为h= =5 m
=5 m
在功率恒定的过程中,最后匀速运动的速率为
vm=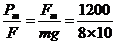 =15 m/s
=15 m/s
外力对物体做的总功W=Pmt2-mgh2,动能变化量为
ΔEk= mv2m-
mv2m- mvt2
mvt2
由动能定理得Pmt2-mgh2= mvm2-
mvm2- mvt2
mvt2
代入数据后解得t2=5.75 s,所以t=t1+t2=7.75 s所需时间至少为7.75 s.
●锦囊妙计
机车起动分两类:(1)以恒定功率起动;(2)以恒定牵引力起动.其解题关键在于逐步分析v、a、F、p间关系,并把握由起动到匀速的临界条件F=f,即汽车达到最大速度的条件.
该类问题的思维流程为:
(1)以恒定功率起动的运动过程是:变加速(a↓)(a=0)匀速,在此过程中,F牵、v、a的变化情况:
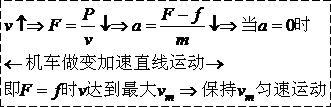

 所以汽车达到最大速度时a=0,F=f,P=Fvm=fvm.
所以汽车达到最大速度时a=0,F=f,P=Fvm=fvm.
 (2)以恒定牵引力匀加速起动的运动过程是:匀加速
(2)以恒定牵引力匀加速起动的运动过程是:匀加速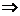 当功率增大到额定功率Pm后,变加速(a↓)
当功率增大到额定功率Pm后,变加速(a↓) 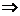 (a=0)匀速.各个量(牵引功率、牵引力、加速度、速度)的变化情况如下:
(a=0)匀速.各个量(牵引功率、牵引力、加速度、速度)的变化情况如下:
●歼灭难点训练
1.(★★★)汽车以恒定功率P由静止出发,沿平直路面行驶,最大速度为v,则下列判断正确的是
A.汽车先做匀加速运动,最后做匀速运动
B.汽车先做加速度越来越大的加速运动,最后做匀速运动
C.汽车先做加速度越来越小的加速运动,最后做匀速运动
D.汽车先做加速运动,再做减速运动,最后做匀速运动
P88页练习第二题的(3)、(4)小题。
课后记:
2. 在本节课的学习过程中,还有哪些不太明白的地方,请向老师提出。
1. 请学生回顾本节课所学知识内容有哪些,所涉及到的主要数学思想又有哪些;
2.P88页练习第二题的(1)、(2)小题
1.学生在教师指导下完成下列例题
例1.
求函数f(x)=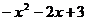 的零点个数。
的零点个数。
问题:
(1)你可以想到什么方法来判断函数零点个数?
(2)判断函数的单调性,由单调性你能得该函数的单调性具有什么特性?
例2.求函数 ,并画出它的大致图象.
,并画出它的大致图象.
师:引导学生探索判断函数零点的方法,指出可以借助计算机或计算器来画函数的图象,结合图象对函数有一个零点形成直观的认识.
生:借助计算机或计算器画出函数的图象,结合图象确定零点所在的区间,然后利用函数单调性判断零点的个数.
4.生:分析函数,按提示探索,完成解答,并认真思考.
师:引导学生结合函数图象,分析函数在区间端点上的函数值的符号情况,与函数零点是否存在之间的关系.
生:结合函数图象,思考、讨论、总结归纳得出函数零点存在的条件,并进行交流、评析.
师:引导学生理解函数零点存在定理,分析其中各条件的作用.
3.零点存在性的探索:
(Ⅰ)观察二次函数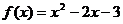 的图象:
的图象:
① 在区间 上有零点______;
上有零点______;
 _______,
_______, _______,
_______,
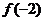 ·
·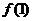 _____0(<或>=).
_____0(<或>=).
② 在区间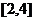 上有零点______;
上有零点______;
 ·
·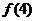 ____0(<或>=).
____0(<或>=).
(Ⅱ)观察下面函数 的图象
的图象
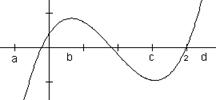
① 在区间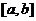 上______(有/无)零点;
上______(有/无)零点;
 ·
· _____0(<或>=).
_____0(<或>=).
② 在区间 上______(有/无)零点;
上______(有/无)零点;
 ·
· _____0(<或>=).
_____0(<或>=).
③ 在区间 上______(有/无)零点;
上______(有/无)零点;
 ·
·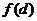 _____0(<或>=).
_____0(<或>=).
由以上两步探索,你可以得出什么样的结论?
怎样利用函数零点存在性定理,断定函数在某给定区间上是否存在零点?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com