
22、(2009年长春市)26.甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后,继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流的速度和水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.
(1)写出乙船在逆流中行驶的速度.(2分)
(2)求甲船在逆流中行驶的路程.(2分)
(3)求甲船到A港的距离y1与行驶时间x之间的函数关系式.(4分)
(4)求救生圈落入水中时,甲船到A港的距离.(2分)
 [参考公式:船顺流航行的速度
[参考公式:船顺流航行的速度 船在静水中航行的速度+水流速度,船逆流航行的速度
船在静水中航行的速度+水流速度,船逆流航行的速度 船在静水中航行的速度
船在静水中航行的速度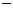 水流速度.]
水流速度.]
20、(德州市二○○九年)20。 (本题满分9分)为了贯彻落实国务院关于促进家电下乡的指示精神,有关部门自2007年12月底起进行了家电下乡试点,对彩电、冰箱(含冰柜)、手机三大类产品给予产品销售价格13%的财政资金直补.企业数据显示,截至2008年12月底,试点产品已销售350万台(部),销售额达50亿元,与上年同期相比,试点产品家电销售量增长了40%.
(1)求2007年同期试点产品类家电销售量为多少万台(部)?
(2)如果销售家电的平均价格为:彩电每台1500元,冰箱每台2000元,手机每部800元,已知销售的冰箱(含冰柜)数量是彩电数量的 倍,求彩电、冰箱、手机三大类产品分别销售多少万台(部),并计算获得的政府补贴分别为多少万元?
倍,求彩电、冰箱、手机三大类产品分别销售多少万台(部),并计算获得的政府补贴分别为多少万元?
解:(1)2007年销量为a万台,则a(1+40%)=350,a =250(万台). ……3分
(2)设销售彩电x万台,则销售冰箱 x万台,销售手机(350-
x万台,销售手机(350- x)万台.由题意得:1500x+2000×
x)万台.由题意得:1500x+2000× +800(350
+800(350 x)=500000. ……………6分
x)=500000. ……………6分
解得x=88. ………………………………………………………7分
∴  ,
, .
.
所以,彩电、冰箱(含冰柜)、手机三大类产品分别销售88万台、132万台、130万部.………………………………………………………………8分
∴ 88×1500×13%=17160(万元),132×2000×13%=34320(万元),
130×800×13%=13520(万元).
获得的政府补贴分别是17160万元、34320万元、13520万元. ……9分
19、(济南市2009年)21.(本小题满分8分)自2008年爆发全球金融危机以来,部分企业受到了不同程度的影响,为落实“促民生、促经济”政策,济南市某玻璃制品销售公司今年1月份调整了职工的月工资分配方案,调整后月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售的件数).下表是甲、乙两位职工今年五月份的工资情况信息:
|
职工 |
甲 |
乙 |
|
月销售件数(件) |
200 |
180 |
|
月工资(元) |
1800 |
1700 |
(1)试求工资分配方案调整后职工的月基本保障工资和销售每件产品的奖励金额各多少元?
(2)若职工丙今年六月份的工资不低于2000元,那么丙该月至少应销售多少件产品?
解:(1)设职工的月基本保障工资为 元,销售每件产品的奖励金额为
元,销售每件产品的奖励金额为 元·················· 1分
元·················· 1分
由题意得 ··················································································· 3分
··················································································· 3分
解这个方程组得 ······················································································ 4分
······················································································ 4分
答:职工月基本保障工资为800元,销售每件产品的奖励金额5元.······························ 5分
(2)设该公司职工丙六月份生产 件产品····································································· 6分
件产品····································································· 6分
由题意得 ··················································································· 7分
··················································································· 7分
解这个不等式得
答:该公司职工丙六月至少生产240件产品 8分
18、(济宁市二○○九年)25.(9分)某体育用品商店购进一批滑板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)求商家降价前每星期的销售利润为多少元?
(2)降价后,商家要使每星期的销售利润最大,应将售价定为多少元?最大销售利润是多少?
解:(1) (130-100)×80=2400(元);…………………………………4分
(2)设应将售价定为 元,则销售利润
元,则销售利润
 ……………………………………6分
……………………………………6分

 .……………………………………………8分
.……………………………………………8分
当 时,
时, 有最大值2500.
有最大值2500.
∴应将售价定为125元,最大销售利润是2500元. ……………9分
17、 (2009年临沂市)24.(本小题满分10分)在全市中学运动会800m比赛中,甲乙两名运动员同时起跑,刚跑出200m后,甲不慎摔倒,他又迅速地爬起来继续投入比赛,并取得了优异的成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系,根据图像解答下列问题:
(2009年临沂市)24.(本小题满分10分)在全市中学运动会800m比赛中,甲乙两名运动员同时起跑,刚跑出200m后,甲不慎摔倒,他又迅速地爬起来继续投入比赛,并取得了优异的成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系,根据图像解答下列问题:
(1)甲摔倒前,________的速度快(填甲或乙);
(2)甲再次投入比赛后,在距离终点多远处追上乙?
解:(1)甲.········································································································· (3分)
(2)设线段 的解析式为
的解析式为 .
.
把 代入
代入 ,得
,得 .
.
 线段
线段 的解析式为
的解析式为 (
( ).··············································· (5分)
).··············································· (5分)
设线段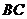 的解析式为
的解析式为 .
.
把 ,
, 分别代入
分别代入 .
.
得 解得
解得
 线段
线段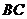 的解析式为
的解析式为 (
( ).····································· (7分)
).····································· (7分)
解方程组 得
得 ······························································· (9分)
······························································· (9分)
 .
.
答:甲再次投入比赛后,在距离终点 处追上了乙. (10分)
处追上了乙. (10分)
16、(泰安市2009年)23(本小题满分10分)某旅游商品经销店欲购进A、B两种纪念品,若用380元购进A种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件,B种纪念品6件。
(1) 求A、B两种纪念品的进价分别为多少?
(2) 若该商店每销售1件A种纪念品可获利5元,每销售1件B种纪念品可获利7元,该商店准备用不超过900元购进A、B两种纪念品40件,且这两种纪念品全部售出候总获利不低于216元,问应该怎样进货,才能使总获利最大,最大为多少?
解:(1)设A、B两种纪念品的进价分别为x元、y元。

由题意, 得 ………… 2分

解之,得… …4分
答:A、B两种纪念品的进价分别为20元、30元… …… …5分
(2)设上点准备购进A种纪念品a件,则购进B种纪念品(40-x)件,

由题意,得
… …… …… ……7分
解之,得: … ………………………………………………8分
… ………………………………………………8分
∵总获利 是a的一次函数,且w随a的增大而减小
是a的一次函数,且w随a的增大而减小
∴当a=30时,w最大,最大值w=-2×30+280=220.
∴40-a=10
∴应进A种纪念品30件,B种纪念品10件,在能是获得利润最大,最大值是220元。………………………………………………………………………………10分
15、(威海市2009年)22.(10分)响应“家电下乡”的惠农政策,某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台,其中甲种电冰箱的台数是乙种电冰箱台数的2倍,购买三种电冰箱的总金额不超过132 000元.已知甲、乙、丙三种电冰箱的出厂价格分别为:1 200元/台、1 600元/台、2 000元/台.
(1)至少购进乙种电冰箱多少台?
(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数,则有哪些购买方案?
解:(1)设购买乙种电冰箱 台,则购买甲种电冰箱
台,则购买甲种电冰箱 台,
台,
丙种电冰箱 台,根据题意,列不等式:·························································· 1分
台,根据题意,列不等式:·························································· 1分
 .······················································· 3分
.······················································· 3分
解这个不等式,得 .·························································································· 4分
.·························································································· 4分
 至少购进乙种电冰箱14台.······················································································ 5分
至少购进乙种电冰箱14台.······················································································ 5分
(2)根据题意,得 .·············································································· 6分
.·············································································· 6分
解这个不等式,得 .·························································································· 7分
.·························································································· 7分
由(1)知 .
.  . 又
. 又 为正整数,
为正整数,
 .··········································································································· 8分
.··········································································································· 8分
所以,有三种购买方案:
方案一:甲种电冰箱为28台,乙种电冰箱为14台,丙种电冰箱为38台;
方案二:甲种电冰箱为30台,乙种电冰箱为15台,丙种电冰箱为35台;
方案三:甲种电冰箱为32台,乙种电冰箱为16台,丙种电冰箱为32台. 10分
14、(2009年烟台市)23.(本题满分10分)某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
解:(1)根据题意,得 ,
,
即 .······················································································ 2分
.······················································································ 2分
(2)由题意,得 .
.
整理,得 .················································································ 4分
.················································································ 4分
解这个方程,得 .·········································································· 5分
.·········································································· 5分
要使百姓得到实惠,取 .所以,每台冰箱应降价200元.································· 6分
.所以,每台冰箱应降价200元.································· 6分
(3)对于 ,
,
当 时,······················································································ 8分
时,······················································································ 8分
 .
.
所以,每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元. 10分
13、(2009年山西省太原市)28.(本小题满分9分)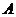 、
、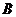 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往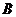 城,乙车驶往
城,乙车驶往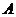 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距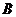 城高速公路入口处的距离
城高速公路入口处的距离 (千米)与行驶时间
(千米)与行驶时间 (时)之间的关系如图.
(时)之间的关系如图.
(1)求 关于
关于 的表达式;
的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为 (千米).请直接写出
(千米).请直接写出 关于
关于 的表达式;
的表达式;
 (3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为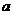 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度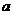 .在下图中画出乙车离开
.在下图中画出乙车离开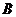 城高速公路入口处的距离
城高速公路入口处的距离 (千米)与行驶时间
(千米)与行驶时间 (时)之间的函数图象.
(时)之间的函数图象.
解:(1)方法一:由图知 是
是 的一次函数,设
的一次函数,设 ········································ 1分
········································ 1分
 图象经过点(0,300),(2,120),∴
图象经过点(0,300),(2,120),∴ ··························· 2分
··························· 2分
解得 ························································································ 3分
························································································ 3分
∴ 即
即 关于
关于 的表达式为
的表达式为 ····················· 4分
····················· 4分
方法二:由图知,当 时,
时, ;
; 时,
时,
所以,这条高速公路长为300千米.
甲车2小时的行程为300-120=180(千米).
∴甲车的行驶速度为180÷2=90(千米/时).··········································· 3分
∴ 关于
关于 的表达式为
的表达式为 (
( ).······················ 4分
).······················ 4分
(2) ······················································································ 5分
······················································································ 5分
(3)在 中.当
中.当 时,
时,
即甲乙两车经过2小时相遇.············································································· 6分
 在
在 中,当
中,当 .所以,相遇后乙车到达终点所用的时间为
.所以,相遇后乙车到达终点所用的时间为 (小时).
(小时).
乙车与甲车相遇后的速度
 (千米/时).
(千米/时).
∴ (千米/时).··································· 7分
(千米/时).··································· 7分
乙车离开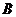 城高速公路入口处的距离
城高速公路入口处的距离 (千米)与行
(千米)与行
驶时间 (时)之间的函数图象如图所示.·············· 9分
(时)之间的函数图象如图所示.·············· 9分
12、(2009年山西省)(24.(本题8分)某批发市场批发甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润 (万元)与进货量
(万元)与进货量 (吨)近似满足函数关系
(吨)近似满足函数关系 ;乙种水果的销售利润
;乙种水果的销售利润 (万元)与进货量
(万元)与进货量 (吨)近似满足函数关系
(吨)近似满足函数关系 (其中
(其中 为常数),且进货量
为常数),且进货量 为1吨时,销售利润
为1吨时,销售利润 为1.4万元;进货量
为1.4万元;进货量 为2吨时,销售利润
为2吨时,销售利润 为2.6万元.
为2.6万元.
(1)求 (万元)与
(万元)与 (吨)之间的函数关系式.
(吨)之间的函数关系式.
(2)如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为 吨,请你写出这两种水果所获得的销售利润之和
吨,请你写出这两种水果所获得的销售利润之和 (万元)与
(万元)与 (吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
(吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
解:(1)由题意,得: 解得
解得 ······················································· (2分)
······················································· (2分)
∴ ····················································································· (3分)
····················································································· (3分)
(2)
∴ ··················································································· (5分)
··················································································· (5分)
 ∴
∴ 时,
时, 有最大值为6.6.
····························· (7分)
有最大值为6.6.
····························· (7分)
∴ (吨).
(吨).
答:甲、乙两种水果的进货量分别为4吨和6吨时,获得的销售利润之和最大,最大利润是6.6万元. (8分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com