
32、(2009年湖北鄂州)26、(10分)某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售。按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,
解答以下问题
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式.
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案。
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值。
解:(1)8x+6y+5(20-x-y)=120
∴y=20-3x ∴y与x之间的函数关系式为y=20-3x ……………………3分
(2)由x≥3,y=20-3x≥3, 20-x-(20-3x)≥3可得
又∵x为正整数 ∴ x=3,4,5 ………………………………………………5分
故车辆的安排有三种方案,即:
方案一:甲种3辆 乙种11辆 丙种6辆
方案二:甲种4辆 乙种8辆 丙种8辆
方案三:甲种5辆 乙种5辆 丙种10辆…………………………7分
(3)设此次销售利润为W元,
W=8x·12+6(20-3x)·16+5[20-x-(20-3x)]·10=-92x+1920
∵W随x的增大而减小 又x=3,4,5
∴ 当x=3时,W最大=1644(百元)=16.44万元
答:要使此次销售获利最大,应采用(2)中方案一,即甲种3辆,乙种11辆,丙种6辆,最大利润为16.44万元。 ……
31、(2009湖北荆州) 24.(10分)由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台,并预付了5万元押金。他计划一年内要达到一定的销售量,且完成此销售量所用的进货总金额加上押金控制在不低于34万元,但不高于40万元.若一年内该产品的售价
24.(10分)由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台,并预付了5万元押金。他计划一年内要达到一定的销售量,且完成此销售量所用的进货总金额加上押金控制在不低于34万元,但不高于40万元.若一年内该产品的售价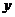 (万元/台)与月次
(万元/台)与月次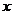 (
(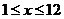 且为整数)满足关系是式:
且为整数)满足关系是式: ,一年后发现实际每月的销售量
,一年后发现实际每月的销售量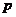 (台)与月次
(台)与月次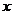 之间存在如图所示的变化趋势.
之间存在如图所示的变化趋势.
⑴ 直接写出实际每月的销售量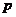 (台)与月次
(台)与月次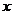 之间
之间
的函数关系式;
⑵ 求前三个月中每月的实际销售利润 (万元)与月
(万元)与月
次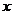 之间的函数关系式;
之间的函数关系式;
⑶ 试判断全年哪一个月的的售价最高,并指出最高售价;
⑷ 请通过计算说明他这一年是否完成了年初计划的销售量.
30、 (2009湖北黄冈)(满分11分)新星电子科技公司积极应对2008年世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线
(2009湖北黄冈)(满分11分)新星电子科技公司积极应对2008年世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线 的一部分,且点A,B,C的横坐标分别为4,10,12
的一部分,且点A,B,C的横坐标分别为4,10,12
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?
29、(黑龙江哈尔滨)26.(本题8分) 跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.

28、(2009河北)25.(本小题满分12分)某公司装修需用A型板材240块、B型板材180块,A型板材规格是60 cm×30 cm,B型板材规格是40 cm×30 cm.现只能购得规格是150 cm×30 cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(图15是裁法一的裁剪示意图)
|
|
裁法一 |
裁法二 |
 裁法三 裁法三 |
|
A型板材块数 |
1 |
2 |
0 |
|
B型板材块数 |
2 |
m |
n |
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y
张、按裁法三裁z张,且所裁出的A、B两种型号的板材刚好够用.
(1)上表中,m = ,n = ;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,
并指出当x取何值时Q最小,此时按三种裁法各裁标准板材
多少张?
解:(1)0 ,3.
(2)由题意,得
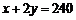 , ∴
, ∴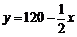 .
. 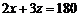 ,∴
,∴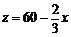 .
.
(3)由题意,得 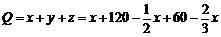 .整理,得
.整理,得  .
.
由题意,得 解得 x≤90.
解得 x≤90.
[注:事实上,0≤x≤90 且x是6的整数倍]由一次函数的性质可知,当x=90时,Q最小.此时按三种裁法分别裁90张、75张、0张.
27、(2009年贵州安顺)24、(本题满分10分)在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1) 小明他们一共去了几个成人,几个学生?
(2) 请你帮助小明算一算,用哪种方式购票更省钱?说明理由。

解:(1)设成人人数为x人,则学生人数为(12-x)人. 则 (1′)
35x +  (12 –x)=
350
(4′)
(12 –x)=
350
(4′)
解得:x = 8 (7′)
故:学生人数为12 – 8 = 4 人, 成人人数为8人. (8′)
(2)如果买团体票,按16人计算,共需费用:
35×0.6×16 = 336元
336﹤350 所以,购团体票更省钱。 (10′)
答:有成人8人,学生4人;购团体票更省钱。
26、(黔东南州2009年)25、(12分)凯里市某大型酒店有包房100间,在每天晚餐营业时间,每间包房收包房费100元时,包房便可全部租出;若每间包房收费提高20元,则减少10间包房租出,若每间包房收费再提高20元,则再减少10间包房租出,以每次提高20元的这种方法变化下去。
(1)设每间包房收费提高x(元),则每间包房的收入为y1(元),但会减少y2间包房租出,请分别写出y1、y2与x之间的函数关系式。
(2)为了投资少而利润大,每间包房提高x(元)后,设酒店老板每天晚餐包房总收入为y(元),请写出y与x之间的函数关系式,求出每间包房每天晚餐应提高多少元可获得最大包房费收入,并说明理由。
解:(1) ………………(1分)
………………(1分)
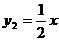 ……………………(3分)
……………………(3分)
(2) ………………(6分)
………………(6分)
即:y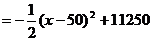 …………………(8分)
…………………(8分)
因为提价前包房费总收入为100×100=10000。
当x=50时,可获最大包房收入11250元,因为11250>10000。又因为每次提价为20元,所以每间包房晚餐应提高40元或60元。…………(12分)
25、(2009年广东广州)23. (本小题满分12分)为了拉动内需,广东启动“家电下乡”活动。某家电公司销售给农户的Ⅰ型冰箱和Ⅱ型冰箱在启动活动前一个月共售出960台,启动活动后的第一个月销售给农户的Ⅰ型和Ⅱ型冰箱的销量分别比启动活动前一个月增长30%、25%,这两种型号的冰箱共售出1228台。
(1)在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别为多少台?
(2)若Ⅰ型冰箱每台价格是2298元,Ⅱ型冰箱每台价格是1999元,根据“家电下乡”的有关政策,政府按每台冰箱价格的13%给购买冰箱的农户补贴,问:启动活动后的第一个月销售给农户的1228台Ⅰ型冰箱和Ⅱ型冰箱,政府共补贴了多少元(结果保留2个有效数字)?
解:(1)在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别为x、y台,得
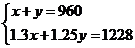
解得 经检验,符合题意。
经检验,符合题意。
答:在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别为560台、400台。
(2)(2298×560×1.3+1999×400×1.25)×13%=3.5×105
24、
 (2009年安徽)(本题满分14分)23.已知某种水果的批发单价与批发量的函数关系如图(1)所示.(1)请说明图中①、②两段函数图象的实际意义.
(2009年安徽)(本题满分14分)23.已知某种水果的批发单价与批发量的函数关系如图(1)所示.(1)请说明图中①、②两段函数图象的实际意义.

(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.
(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.
(1)解:图①表示批发量不少于20kg且不多于60kg的该种水果,(1)解:图①表示批发量不少于20kg且不多于60kg的该种水果,可按5元/kg批发;……3分
图②表示批发量高于60kg的该种水果,可按4元/kg批发.
………………………………………………………………3分
 (2)解:由题意得:
(2)解:由题意得: ,函数图象如图所示.
,函数图象如图所示.
………………………………………………………………7分
由图可知资金金额满足240<w≤300时,以同样的资金可
批发到较多数量的该种水果.……………………………8分
(3)解法一:
设当日零售价为x元,由图可得日最高销量
当m>60时,x<6.5
由题意,销售利润为
 ………………………………12分
………………………………12分
当x=6时, ,此时m=80
,此时m=80
即经销商应批发80kg该种水果,日零售价定为6元/kg,
当日可获得最大利润160元.……………………………………………14分
解法二:
设日最高销售量为xkg(x>60)
则由图②日零售价p满足: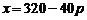 ,于是
,于是
销售利润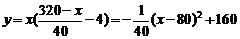 ………………………12分
………………………12分
当x=80时, ,此时p=6
,此时p=6
即经销商应批发80kg该种水果,日零售价定为6元/kg,
当日可获得最大利润160元.……………………………………………14分
23、(2009年湖南省株洲市)23.(本题满分10分)初中毕业了,孔明同学准备利用暑假卖报纸赚取140-200元钱,买一份礼物送给父母.已知:在暑假期间,如果卖出的报纸不超过1000份,则每卖出一份报纸可得0.1元;如果卖出的报纸超过1000份,则超过部分每份可得0.2元.
(1)请说明:孔明同学要达到目的,卖出报纸的份数必须超过1000份.
(2)孔明同学要通过卖报纸赚取140-200元,请计算他卖出报纸的份数在哪个范围内.
解:(1)如果孔明同学卖出1000份报纸,则可获得: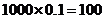 元,没有超过140元,从而不能达到目的.(注:其它说理正确、合理即可.)
……… 3分
元,没有超过140元,从而不能达到目的.(注:其它说理正确、合理即可.)
……… 3分
(2)设孔明同学暑假期间卖出报纸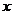 份,由(1)可知
份,由(1)可知 ,依题意得:
,依题意得:
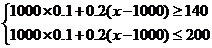 ………………………7分
………………………7分
解得
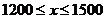 ……………………9分
……………………9分
答:孔明同学暑假期间卖出报纸的份数在1200-1500份之间. ……………………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com