
1、向量有关概念:
(1)向量的概念:既有大小又有方向的量,注意向量和数量的区别。向量常用有向线段来表示,注意不能说向量就是有向线段,为什么?(向量可以平移)。如已知A(1,2),B(4,2),则把向量 按向量
按向量 =(-1,3)平移后得到的向量是_____(答:(3,0))
=(-1,3)平移后得到的向量是_____(答:(3,0))
(2)零向量:长度为0的向量叫零向量,记作: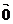 ,注意零向量的方向是任意的;
,注意零向量的方向是任意的;
(3)单位向量:长度为一个单位长度的向量叫做单位向量(与 共线的单位向量是
共线的单位向量是 );
);
(4)相等向量:长度相等且方向相同的两个向量叫相等向量,相等向量有传递性;
(5)平行向量(也叫共线向量):方向相同或相反的非零向量 、
、 叫做平行向量,记作:
叫做平行向量,记作: ∥
∥ ,规定零向量和任何向量平行。提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有
,规定零向量和任何向量平行。提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有 );④三点
);④三点 共线
共线
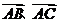 共线;
共线;
(6)相反向量:长度相等方向相反的向量叫做相反向量。 的相反向量是-
的相反向量是- 。
。
如下列命题:(1)若 ,则
,则 。(2)两个向量相等的充要条件是它们的起点相同,终点相同。(3)若
。(2)两个向量相等的充要条件是它们的起点相同,终点相同。(3)若 ,则
,则 是平行四边形。(4)若
是平行四边形。(4)若 是平行四边形,则
是平行四边形,则 。(5)若
。(5)若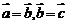 ,则
,则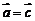 。(6)若
。(6)若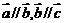 ,则
,则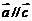 。其中正确的是_______(答:(4)(5))
。其中正确的是_______(答:(4)(5))
42、(2009湖南株洲)20.(本题满分10分)初中毕业了,孔明同学准备利用暑假卖报纸赚取140-200元钱,买一份礼物送给父母.已知:在暑假期间,如果卖出的报纸不超过1000份,则每卖出一份报纸可得0.1元;如果卖出的报纸超过1000份,则超过部分每份可得0.2元.
(1)请说明:孔明同学要达到目的,卖出报纸的份数必须超过1000份.
(2)孔明同学要通过卖报纸赚取140-200元,请计算他卖出报纸的份数在哪个范围内.
解:(1)如果孔明同学卖出1000份报纸,则可获得: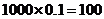 元,没有超过140元,从而不能达到目的.(注:其它说理正确、合理即可.)
……… 3分
元,没有超过140元,从而不能达到目的.(注:其它说理正确、合理即可.)
……… 3分
(2)设孔明同学暑假期间卖出报纸 份,由(1)可知
份,由(1)可知 ,依题意得:
,依题意得:
 ………………………7分
………………………7分
解得
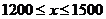 ……………………9分
……………………9分
答:孔明同学暑假期间卖出报纸的份数在1200-1500份之间. ……………………10分
41、(2009年湖南益阳)18.(10分) 开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不少于钢笔数,共有多少种购买方案?请你一一写出.
解:(1)设每支钢笔x元,每本笔记本y元····································································· 1分
依题意得: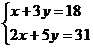 ········································································· 3分
········································································· 3分
解得: ·························································································· 4分
·························································································· 4分
答:每支钢笔3元,每本笔记本5元························································ 5分
(2)设买a支钢笔,则买笔记本(48-a)本
依题意得: ·························································· 7分
·························································· 7分
解得: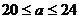 ··············································································· 8分
··············································································· 8分
所以,一共有5种方案.·········································································· 9分
即购买钢笔、笔记本的数量分别为:
20,28; 21,27; 22,26; 23,25; 24,24. 10分
40、(2009湖南娄底)18.(本小题7分)娄底至新化高速公路的路基工程分段招标,市路桥公司中标承包了一段
路基工程,进入施工场地后,所挖筑路基的长度y(m)与挖筑时间x(天)之间的函
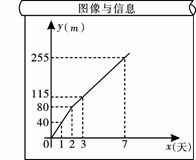 数关系如图所示,请根据提供的信息解答下列问题:(1)请你求出:
数关系如图所示,请根据提供的信息解答下列问题:(1)请你求出:
①在0≤x<2的时间段内,y与x的函数关系式;
②在x≥2时间段内,y与x的函数关系式.
(2)用所求的函数解析式预测完成1620 m的路基工
程,需要挖筑多少天?
解:(1)当0≤x<2时,设y与x的函数关系式为y=kx……………………………1分
∴40=k
∴y与x的函数式为y=40x(0≤x<2)………………………………………2分
(2)当x≥2时,设y与x的函数式为y=kx+b………………………………3分

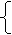 115=3k+b
115=3k+b
255=7k+b
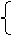
 k=35
k=35
b=10
∴y与x的函数式为y=35x+10(x≥2)……………………………………5分
(3)当y=1620时,35x+10=1620
x=46…………………………………………………………………………6分
答:需要挖筑46天.…………………………………………………………7分
39、(2009湖南娄底)22.(本小题8分)为了加快社会主义新农村建设,让农民享受改革开放30年取得的成果,
党中央、国务院决定:凡农民购买家电和摩托车享受政府13%的补贴(凭购物发票到
乡镇财政所按13%领取补贴). 星星村李伯伯家今年购买了一台彩电和一辆摩托车共花
去6000元,且该辆摩托车的单价比所买彩电的单价的2倍还多600元.
(1)李伯伯可以到乡财政所领到的补贴是多少元?
(2)求李伯伯家所买的摩托车与彩电的单价各是多少元?
解:(1)6000×13%=780……………………………………………………1分
答:李伯伯可以从政府领到补贴780元………………………………2分
(2)方法一:设彩电的单价为x元/台……………………………………3分
x+2x+600=6000…………………………………………………………5分
3x=5400
x=1800……………………………………………………………………6分
2x+600=2×1800+600=4200………………………………………………7分
答:彩电与摩托车的单价分别为1800元/台、4200元/辆……………………8分
方法二:设买摩托车的单价为x元/辆,彩电单价为y元/台………………3分
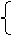
 x+y=6000
x+y=6000
x=2y+600


 x=4200
x=4200
y=18007
答:彩电与摩托车的单价分别为1800元/台、4200元/辆………………8分
38、(2009湖南衡阳)24、(本小题满分8分)在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),图10中的折线分别表示S1、S2与t之间的函数关系.
(1)甲、乙两地之间的距离为 8 km,乙、丙两地之间的距离为 2 km;

 (2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.
解:(2)第二组由甲地出发首次到达乙地所用的时间为:
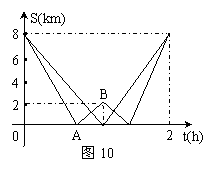
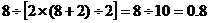 (小时)
(小时)
第二组由乙地到达丙地所用的时间为:
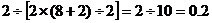 (小时)
(小时)
(3)根据题意得A、B的坐标分别为(0.8,0)
和(1,2),设线段AB的函数关系式为:
 ,根据题意得:
,根据题意得:
 解得:
解得: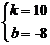
∴图中线段AB所表示的S2与t间的函数关系式为: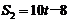 ,自变量t的取值范围是:
,自变量t的取值范围是: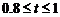 .
.
37、(2009年湖南长沙)23.(本题满分8分)某中学拟组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”
小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?
解:(1)设平安公司60座和45座客车每天每辆的租金分别为 元,
元, 元.·················· 1分
元.·················· 1分
由题意,列方程组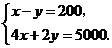 ············································································· 5分
············································································· 5分
解之得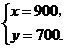 ·········································································································· 7分
·········································································································· 7分
(2)九年级师生共需租金: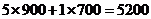 (元)········································· 8分
(元)········································· 8分
答:(略)
36、(2009湖北孝感)24.(本题满分10分)五月份,某品牌衬衣正式上市销售,5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为0.设该品牌衬衣的日销售量为P(件),销售日期为n(日),P与n之间的关系如图所示.
(1)写出P关于n的函数关系式P= (注明n的取值范围);(3分)
 (2)经研究表明,该品牌衬衣的日销售量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?(4分)
(2)经研究表明,该品牌衬衣的日销售量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?(4分)
(3)该品牌衬衣本月共销售了 件.(3分)
解:(1)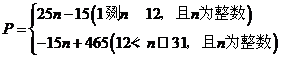 ······················································· 3分
······················································· 3分
(2)由题意,有: ······································································· 5分
······································································· 5分
解得 整数
整数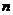 的值可取7,8,9……20共14个.
的值可取7,8,9……20共14个.
∴该品牌衬衣本月在市面的流行期为14天.························································· 7分
(3)4335件.
34、(2009年湖北武汉)23.(本题满分10分)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨 元(
元( 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为 元.
元.
(1)求 与
与 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
解:(1) (
(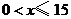 且
且 为整数);
为整数);
(2)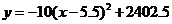 .
.
 ,
, 当
当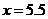 时,
时, 有最大值2402.5.
有最大值2402.5.
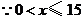 ,且
,且 为整数,
为整数,
当 时,
时,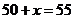 ,
,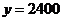 (元),当
(元),当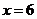 时,
时,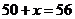 ,
,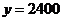 (元)
(元)
 当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
(3)当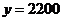 时,
时,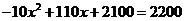 ,解得:
,解得: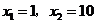 .
.
 当
当 时,
时, ,当
,当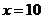 时,
时, .
.
 当售价定为每件51或60元,每个月的利润为2200元.
当售价定为每件51或60元,每个月的利润为2200元.
当售价不低于51或60元,每个月的利润为2200元.
当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元).
35、(2009年湖北仙桃、天门、潜江、江汉油田)22.(本题满分10分)宏志中学九年级300名同学毕业前夕给灾区90名同学捐赠了一批学习用品(书包和文具盒),由于零花钱有限,每6人合买一个书包,每2人合买一个文具盒(每个同学都只参加一件学习用品的购买),书包和文具盒的单价分别是54元和12元.
(1)若有x名同学参加购买书包,试求出购买学习用品的总件数y与x之间的函数关系式(不要求写出自变量的取值范围);
(2)若捐赠学习用品总金额超过了2300元,且灾区90名同学每人至少得到了一件学习用品,请问同学们如何安排购买书包和文具盒的人数?此时选择其中哪种方案,使购买学习用品的总件数最多?
33、(2009湖北黄石)23、(本小题8分)一辆客车从甲地开往甲地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图12所示:
(1)根据图象,直接写出y1,y2关于x的函数关系式。
(2)分别求出当x=3,x=5,x=8时,两车之间的距离。
(3)若设两车间的距离为S(km),请写出S关于x的函数关系式。
 (4)甲、乙两地间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油。求A加油站到甲地的距离。
(4)甲、乙两地间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油。求A加油站到甲地的距离。
解:(1)y1=60x(0≤x≤10)
y2=-100x+600(0≤x≤6) ………(1分)
(2)当x=3时 y1=180 y2=300 ∴y2-y1=120
当x=5时 y1=300 y2=100 ∴y1-y2=200
当x=8时 y1=480 y2=0 ∴y1-y2=y1=480 ……(1分)
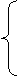 (3)
1600x+600 (0≤x≤
(3)
1600x+600 (0≤x≤ )
)
S= 1600x-600 ( ≤x≤6)
≤x≤6)
60x (6≤x≤10) ………(3分)
(4)由题意得:S=200
①当0≤x≤ 时 -160x+600=200 ∴x=
时 -160x+600=200 ∴x=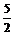 ∴y1=60x=150km
∴y1=60x=150km
②当 ≤x≤6时 160x-600=200 ∴x=5 ∴y1=300km
≤x≤6时 160x-600=200 ∴x=5 ∴y1=300km
③当6≤x≤10时 60x≥360 不合题意
即:A加油站到甲地距离为150km或300km。 ………(3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com