
4. (2006湖北)接种某疫苗后,出现发热反应的概率为0.80.现有5人接种该疫苗,至少有3人出现发热反应的概率为___________.(精确到0.01)
3.(2004辽宁)甲、乙两人独立地解同一问题,甲解决这个问题的概率是p1,乙解决这个问题的概率是p2,那么恰好有1人解决这个问题的概率是 ( )
A. p1p2 B.p1(1-p2)+p2(1-p1)
C.1-p1p2 D.1-(1-p1)(1-p2)
1.从应届高中生中选出飞行员,已知这批学生体型合格的概率为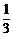 ,视力合格的概率为
,视力合格的概率为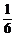 ,其他几项标准合格的概率为
,其他几项标准合格的概率为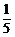 ,从中任选一学生,则该生三项均合格的概率为(假设三项标准互不影响) ( )
,从中任选一学生,则该生三项均合格的概率为(假设三项标准互不影响) ( )
A.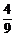 B.
B.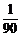 C.
C.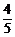 D.
D.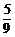
2 (2005天津)某人射击一次击中的概率为0.6,经过3次射击,此人至少有两次击中目标的概率为 ( )
A.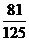 B.
B.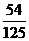 C.
C.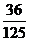 D.
D.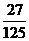
6.独立重复试验的概率公式:如果在一次试验中某事件发生的概率是p,那么在n次独立重复试验中这个事恰好发生K次的概率: .
.
k=n时,即在n次独立重复试验中事件A全部发生,概率为Pn(n)=Cnnpn(1-p)0 =pn
k=0时,即在n次独立重复试验中事件A没有发生,概率为Pn(0)=Cn0p0(1-p)n =(1-p)n
4.独立重复试验的定义:在同样条件下进行的各次之间相互独立的一种试验.
2.互斥事件与相互独立事件是有区别的:
互斥事件与相互独立事件研究的都是两个事件的关系,但而互斥的两个事件是一次实验中的两个事件,相互独立的两个事件是在两次试验中得到的,注意区别。
如果A、B相互独立,则P(A+B)=P(A)+P(B)―P(A B)
B)
如:某人射击一次命中的概率是0.9,射击两次,互不影响,至少命中一次的概率是0.9+0.9-0.9×0.9=0.99,(也即1-0.1×0.1=0.99)
3.相互独立事件同时发生的概率: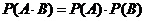
事件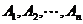 相互独立,
相互独立, 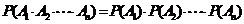
1.相互独立事件:事件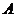 (或
(或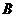 )是否发生对事件
)是否发生对事件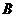 (或
(或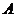 )发生的概率没有影响,这样的两个事件叫做相互独立事件.
)发生的概率没有影响,这样的两个事件叫做相互独立事件.
若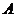 与
与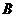 是相互独立事件,则
是相互独立事件,则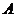 与
与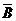 ,
,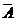 与
与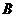 ,
,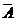 与
与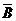 也相互独立.
也相互独立.
2.会计算事件在n次独立重复试验中恰好发生κ次的概率.
1.了解相互独立事件的意义,会用相互独立事件的概率乘法公式计算一些事件的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com