2、追及是指两物体同向运动而达到同一位置。找出两者的时间关系、位移关系是解决追及问题的关键，同时追及物与被追及物的速度恰好相等时临界条件，往往是解决问题的重要条件：

(1)、匀减速物体追及同向匀速物体时，恰能追上或恰好追不上的临界条件为：即将靠近时，追及者速度等于被追及者的速度；

(2)初速度为零的匀加速直线运动的物体追赶同向匀速直线运动的物体时，追上之前距离最大的条件：为两者速度相等

例题分析：

例1、一列快车正以20m/s的速度在平直轨道上运动时，发现前方180m处有一货车正以6m/s速度匀速同向行驶，快车立即制动，快车作匀减速运动，经40s才停止，问是否发生碰车事故？(会发生碰车事故)

例2、同一高度有AB两球，A球自由下落5米后，B球以12米/秒竖直投下，问B球开始运动后经过多少时间追上A球。从B球投下时算起到追上A球时，AB下落的高度各为多少？(g=10m/s²)(2.5秒；61.25米)

例3、AB两辆汽车行驶在一条平直公路上，A车在B车后面以速度V做匀速运动，B车在前面做初速度为零的匀加速运动，加速度为a，两车同向行驶，开始时两车相距为s，为使两车可相遇两次，求V、a、S所满足的关系？

拓展：两车相遇一次或不相遇的条件又是什么呢？

目的要求

　　 复习追击与相遇问题的计算。

知识要点：

1、相遇是指两物体分别从相距S的两地相向运动到同一位置，它的特点是：两物体运动的距离之和等于S，分析时要注意：

(1)、两物体是否同时开始运动，两物体运动至相遇时运动时间可建立某种关系；

(2)、两物体各做什么形式的运动；

(3)、由两者的时间关系，根据两者的运动形式建立S=S1+S2方程；

(4)、建立利用位移图象或速度图象分析；

4、形状相同的位移时间图象和速度时间图象，

物理意义完全不同，可以从下列例题中加以理解。

例题分析：

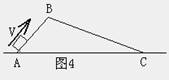
例1、有两个光滑固定斜面AB和BC，A、C两点在同一水平面上，

斜面BC比AB长(如图4所示)，下面四个图中(如图5)正确表

示滑块速率随时间t变化规律的是：

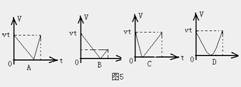
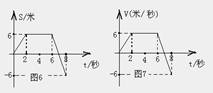
例2、AB两物体同时同地沿同一方向运动，如图6所示为A物体

沿直线运动时的位置与时间关系图，如图7为B物体沿直线运动的速度时间图试问：(1)AB两物体在0--8秒内的运动情况；(2)AB两物体在8秒内的总位移和总路程分别是多少？

例3、如图8所示中AB是一对平行的金属板，在B板加如图9的方波电压，在0~T/2时间内U_B=U₀>0,现有一电子从A板上的小孔进入两板间的电场区内,设电子的初速、重力影响均可忽略,则(　 AB　 )

A、若电子是在t=0时刻进入的，它将一直向B板运动；

B、若电子是在t=T/8时刻进入的，它可能时而向B板运动，时而向A板运动，最后打在B板上；

C、若电子是在t=3T/8时刻进入的，它可能时而向B板运动，时而向A板运动，最后打在B板上；

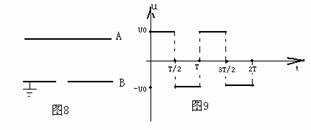　 D、若电子是在t=T/2时刻进入的，它可能时而向B板运动

3、匀变速直线运动的速度--时间图象(υ-t图)

匀变速直线运动的速度是时间的一次函数，即

υ_t=υ₀+at

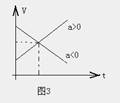　 所对应的是一条直线，如图3所示。由图可求出任意时刻的速度，或根据速度求出时间，还可以求出任意时间所通过的位移，还可以求出匀变速直线运动的加速度a=△υ/△t=直线的斜率K，直线的斜率越大，

即直线越陡，则对就的加速度越大。

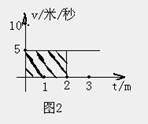
2、匀速直线运动的速度--时间图象(υ-t图)

匀速运动的速度不随时间而变化，因此其图象是一条与时间轴平行的直线，如图2所示，利用υ-t图象可求出任意时刻对应的位移，也就是等于这个矩形的面积。

目的要求：

明确s-t，v-t图象的物理意义

知识要点：

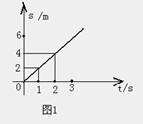
1、匀速直线运动的位移--时间图象(S-t图)

匀速直线运动的位移S与时间t成正比，即S=υt，因此其图象是过原点的直线。由图象可求出任意时间内的位移，如图1可知，1秒末图象对应的位移为2米，应用图也可以求出通过任一位移所需的时间。由图象还可以求物体匀速运动的速度。υ=△s/△t=2m/s，图中直线的斜率表示物体匀速运动的速度，K=υ=△s/△t。

2、竖直上抛运动：物体上获得竖直向上的初速度υ₀后仅在重力作用下的运动。

特点：只受重力作用且与初速度方向反向，以初速方向为正方向则a=-g

υ_t=υ₀-gt

运动规律： h=υ₀t-gt²/2

υ_t²=υ_t²-2gh

对于竖直上抛运动，有分段分析法和整体法两种处理方法。分段法以物体上升到最高点为运动的分界点，根据可逆性可得t_上=t_下=υ₀/g，上升最大高度H=υ₀²/2g，同一高度速度大小相等，方向相反。整体法是以抛出点为计时起点，速度、位移用下列公式求解：

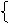υ_t=υ₀-gt

h=υ₀t-gt²/2

注意：若物体在上升或下落中还受有恒空气阻力，则物体的运动不再是自由落体和竖直上抛运动，分别计算上升a_上与下降a_下的加速度，利用匀变速运动公式问题同样可以得到解决。

例题分析：

例1、从距地面125米的高处，每隔相同的时间由静止释放一个小球队，不计空气阻力，g=10米/秒²，当第11个小球刚刚释放时，第1个小球恰好落地，试求：

(1)相邻的两个小球开始下落的时间间隔为多大？

(2)当第1个小球恰好落地时，第3个小球与第5个小球相距多远？

(拓展)将小球改为长为5米的棒的自由落体，棒在下落过程中不能当质点来处理，但可选棒上某点来研究。

例2、在距地面25米处竖直上抛一球，第1秒末及第3秒末先后经过抛出点上方15米处，试求：

(1)上抛的初速度，距地面的最大高度和第3秒末的速度；

(2)从抛出到落地所需的时间(g=10m/s²)

例3、一竖直发射的火箭在火药燃烧的2S内具有3g的竖直向上加速度，当它从地面点燃发射后，它具有的最大速度为多少？它能上升的最大高度为多少？从发射开始到上升的最大高度所用的时间为多少？(不计空气阻力。G=10m/s²)

目的要求

　　 复习自由落体运动的规律。

知识要点：

1、自由落体运动：物体仅在重力作用下由静止开始下落的运动

特点：只受重力作用，即a=g。从静止开始，即υ₀=0

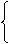υ_t=gt

运动规律： S=gt²/2

υ_t²=2gh

对于自由落体运动，物体下落的时间仅与高度有关，与物体受的重力无关。

3、对于匀减速直线运动，必须特别注意其特性：

(1)匀减速直线运动总有一个速度为零的时刻，此后，有的便停下来，有些会反向匀加速

(2)匀减速运动的反向运动既可以按运动的先后顺序进行运算，也可将返回的运动按初速为零的匀加速运动计算。

例题分析：

例1、关于加速度与速度、位移的关系，以下说法正确的是：(D)

A、υ₀为正，a为负，则速度一定在减小，位移也一定在减小；

B、υ₀为正，a为正，则速度一定在增加，位移不一定在增加；

C、υ₀与a同向，但a逐渐减小，速度可能也在减小；

D、υ₀与a反向，但a逐渐增大，则速度减小得越来越快(在停止运动前)

例2、水平导轨AB的两端各有一竖直的挡板A和B，AB=4米，物体自A开始以4m/s的速度沿导轨向B运动，已知物体在碰到A或B以后，均以与挡板碰前大小相等的速度反弹回来，并且物体在导轨上作匀减速运动的加速度大小相同，为了使物体最终能停在AB的中点，则这个加速度的大小应为多少？

例3、一列车共20节车箱，它从车站匀加速开出时，前5节车厢经过站在车头旁边的人的时间为t秒，那么：

(1)第三个5节车厢经过人的时间为多少？

(2)若每节车厢长为L，则车尾经过人时的速度多大？

(3)车正中点经过人时速度为多大？

(4)车经过人身旁总时间为多少？

答案：例2：-4/(2n+1)例3：略

2、匀变速直线运动特点21世纪教育网

(1)、做匀变速直线运动的物体，在某段时间内的平均速度等于这段时间内的中间时刻的即时速度。21世纪教育网

(2)、匀变速直线运动某段位移中点的即时速度，等于这段位移两端的即时速度的几何平均值。21世纪教育网

(3)、做匀变速直线运动的物体,如果在各个连续相等的时间T内的位移分别为21世纪教育网

s_Ⅰ,s_Ⅱ,s_Ⅲ,……s_n 则:21世纪教育网

△s=s_Ⅱ-s_Ⅰ=s_Ⅲ-s_Ⅱ=……=aT^{221世纪教育网}

(4)、初速为零的匀变速直线运动的特征：(设t为单位时间)21世纪教育网

①1t末，2t末，3t末……即时速度的比为:21世纪教育网

υ₁：υ₂：υ₃：……υn=1:2:3:……n21世纪教育网

②1t内,2t内,3t内……位移之比为：21世纪教育网

S1：S2：S3：……：Sn=1²：2²：3²：……：n^{221世纪教育网}

③第1t内，第2t内，第3t内……位移之比为：21世纪教育网

S_Ⅰ：S_Ⅱ：S_Ⅲ：．．．Sn=1:3:5:．．．(2n-1)21世纪教育网