
20.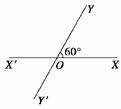 (16分)如图所示,有两条相交成60°角的直路XX′
(16分)如图所示,有两条相交成60°角的直路XX′
和YY′,交点是O,甲、乙分别在OX、OY上,起初
甲离O点3 km,乙离O点1 km,后来两人同时用每小
时4 km的速度,甲沿XX′方向,乙沿Y′Y的方向步行.
(1)起初,两人的距离是多少?
(2)用t表示t小时后两人的距离;
(3)什么时候两人的距离最短?
解 (1)设甲、乙两人起初的位置是A、B,则由余弦定理:
|AB|2=|OA|2+|OB|2-2|OA|·|OB|·cos60°
=32+12-2×3×1×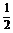 =7,∴|AB|=
=7,∴|AB|=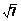 .
.
所以甲、乙两人起初的距离是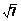 km.
km.
(2)设甲、乙两人t小时后的位置分别是P、Q,
则|AP|=4t,|BQ|=4t,
当0≤t≤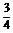 时,由余弦定理
时,由余弦定理
|PQ|2=(3-4t)2+(1+4t)2-2(3-4t)(1+4t)·cos60°,
当t>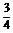 时,
时,
|PQ|2=(4t-3)2+(1+4t)2-2(4t-3)(1+4t)cos120°.
注意到上面两式实际上是统一的,
所以|PQ|2=(16t2-24t+9)+(16t2+8t+1)+(16t2-8t-3)=48t2-24t+7,
即|PQ|=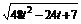 .
.
(3)∵|PQ|=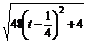 ,
,
∴当t=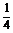 时,|PQ|的最小值是2.
时,|PQ|的最小值是2.
即在第15分钟末,两人的距离最短.
19.(2008·湖南理,19)(16分)在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40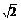 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+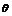 ( 其中sin
( 其中sin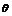 =
=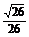 ,0°<
,0°<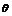 <90°)且与点A相距10
<90°)且与点A相距10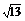 海里的位
海里的位
置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
解 (1)如图(1)所示,AB=40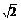 ,
,
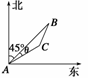 AC=10
AC=10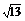 ,∠BAC=
,∠BAC=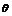 ,sin
,sin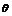 =
=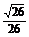 .
.
由于0°<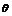 <90°,
<90°,
|
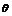 =
= =
=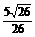 .
.
由余弦定理得
BC=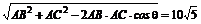 .
.
所以船的行驶速度为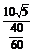 =
=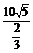 =15
=15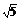 (海里/小时).
(海里/小时).
(2)方法一 如图(2)所示,以A为原点建立平面直角坐标系,设点B、C的坐标分别是B(x1,y1)、C(x2,y2),BC与x轴的交点为D.
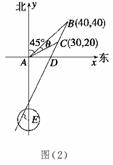 由题设有,
由题设有,
x1=y1=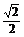 AB=40,
AB=40,
x2=ACcos∠CAD
=10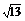 cos(45°-
cos(45°-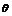 )=30,
)=30,
y2=ACsin∠CAD
=10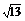 sin(45°-
sin(45°-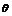 )=20.
)=20.
所以过点B、C的直线l的斜率
k=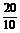 =2,
=2,
直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离
d=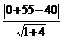 =3
=3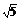 <7,
<7,
所以船会进入警戒水域.
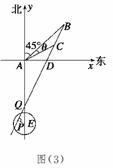 方法二 如图(3)所示,设直线AE
方法二 如图(3)所示,设直线AE
与BC的延长线相交于点Q.
在△ABC中,由余弦定理得
cos∠ABC=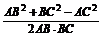
=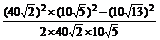
=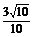 .
.
从而sin∠ABC=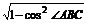
= =
=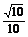 .
.
在△ABQ中,由正弦定理得
AQ=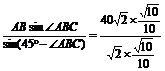 =40.
=40.
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.
过点E作EP⊥BC于点P,则EP为点E到直线BC的距离.
在Rt△QPE中,PE=QE·sin∠PQE=QE·sin∠AQC
=QE·sin(45°-∠ABC)=15×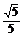 =3
=3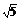 <7.
<7.
所以船会进入警戒水域.
18.(2008·重庆理,17)(16分)设△ABC的内角A,B,C的对边分别为a,b,c,且A=60°,c=3b.求:
(1)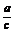 的值;
的值;
(2)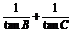 的值.
的值.
解 (1)由余弦定理得
a2=b2+c2-2bccosA
=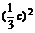 +c2-2·
+c2-2·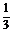 c·c·
c·c·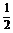 =
=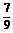 c2,
c2,
故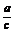 =
=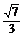 .
.
(2)方法一 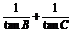 =
=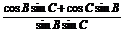
=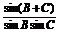 =
=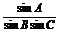 ,
,
由正弦定理和(1)的结论得
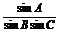 =
=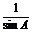 ·
· 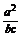 =
=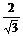 ·
·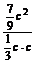 =
=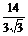 =
=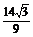 .
.
故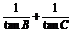 =
=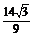 .
.
方法二 由余弦定理及(1)的结论有
cosB=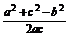 =
=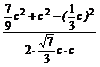 =
=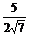 ,
,
故sinB= =
=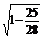 =
=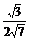 .
.
同理可得
cosC=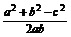 =
=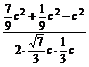 =-
=-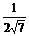 ,
,
sinC=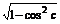 =
=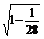 =
=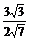 .
.
从而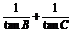 =
=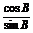 +
+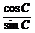
=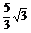 -
-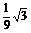 =
=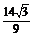 .
.
17.(2009·海安高级中学测试题)(14分)在△ABC中,设A、B、C的对边分别为a、b、c,向量m=(cosA,sinA),
n=(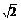 -sinA,cosA),若|m+n|=2.
-sinA,cosA),若|m+n|=2.
(1)求角A的大小;
(2)若b=4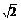 ,且c=
,且c=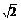 a,求△ABC的面积.
a,求△ABC的面积.
解 (1)m+n=(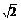 +cosA-sinA,cosA+sinA)
+cosA-sinA,cosA+sinA)
|m+n|2=(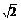 +cosA-sinA)2+(cosA+sinA)2
+cosA-sinA)2+(cosA+sinA)2
=2+2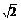 (cosA-sinA)+(cosA-sinA)2+(cosA+sinA)2
(cosA-sinA)+(cosA-sinA)2+(cosA+sinA)2
=2+2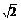 (cosA-sinA)+2
(cosA-sinA)+2
=4-4sin(A-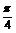 )
)
∵|m+n|=2,∴4-4sin(A-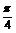 )=4,sin(A-
)=4,sin(A-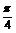 )=0.
)=0.
又∵0<A< ,∴-
,∴-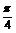 <A-
<A-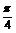 <
<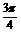 ,∴A-
,∴A-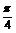 =0,
=0,
∴A=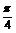 .
.
(2)由余弦定理,a2=b2+c2-2bccosA,
又b=4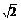 ,c=
,c=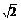 a,A=
a,A=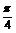 ,
,
得a2=32+2a2-2×4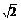 ×
×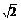 a·
a·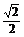 ,
,
即a2-8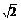 a+32=0,解得a=4
a+32=0,解得a=4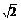 ,∴c=8.
,∴c=8.
∴S△ABC=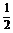 b·csinA=
b·csinA=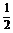 ×4
×4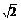 ×8×sin
×8×sin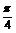 =16.
=16.
S△ABC=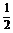 ×(4
×(4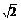 )2=16.
)2=16.
16.(2008·合肥模拟)(14分)已知向量a=(cosx,sinx),|b|=1,且a与b满足|ka+b|=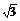 |a-kb| (k>0).
|a-kb| (k>0).
(1)试用k表示a·b,并求a·b的最小值;
(2)若0≤x≤ ,b=
,b=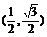 ,求a·b的最大值及相应的x值.
,求a·b的最大值及相应的x值.
解(1)∵|a|=1,|b|=1,
由|ka+b|=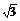 |a-kb|,
|a-kb|,
得(ka+b)2=3(a-kb)2,
整理得a·b= =
=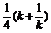 ≥
≥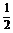 ,
,
当且仅当k=1时,a·b取最小值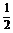 .
.
(2)由a·b=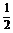 cosx+
cosx+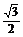 sinx=sin(x+
sinx=sin(x+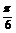 ).
).
∵0≤x≤ ,∴
,∴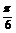 ≤x+
≤x+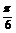 ≤
≤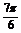 ,
,
∴-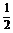 ≤sin(x+
≤sin(x+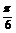 )≤1.
)≤1.
当x=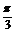 时,a·b取最大值为1.
时,a·b取最大值为1.
15.(14分)设a=(-1,1),b=(4,3),c=(5,-2),
(1)求证a与b不共线,并求a与b的夹角的余弦值;
(2)求c在a方向上的投影;
(3)求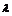 1和
1和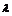 2,使c=
2,使c=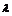 1a+
1a+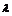 2b.
2b.
(1)证明 ∵a=(-1,1),b=(4,3),-1×3≠1×4,
∴a与b不共线,设a与b的夹角为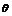 ,
,
cos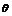 =
= =
=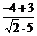 =-
=-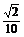 .
.
(2)解 设a与c的夹角为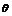 ,
,
cos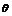 =
= =
=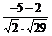 =-
=-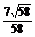 ,
,
∴c在a方向上的投影为
|c|cos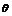 =-
=-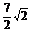 .
.
(3)解 ∵c=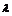 1a+
1a+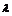 2b,∴
2b,∴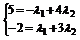 ,
,
解得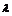 1=-
1=-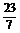 ,
,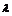 2=
2=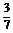 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com