
3.函数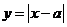 的图象关于直线
的图象关于直线 对称.则
对称.则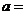 _____________.
_____________.
2.已知函数 的定义域和值域都是
的定义域和值域都是 ,则实数a的值是
________
,则实数a的值是
________
1.函数 的定义域是____________________.
的定义域是____________________.
补充:⑴ =
= 是以(
是以( ,
,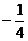 )为顶点、对称轴平行于y轴、开口向上的抛物线(如图);它的单调区间是(-
)为顶点、对称轴平行于y轴、开口向上的抛物线(如图);它的单调区间是(- ,
, ]与[
]与[ ,+
,+ 
 );它在(-
);它在(- ,
, ]上是减函数,在[
]上是减函数,在[ ,+
,+  )上是增函数.
)上是增函数.
证明:设 <
<

 ,则
,则
 -
- =
=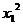 -
-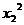 -5(
-5( -
- )
)
 =(
=( +
+ -5) (
-5) ( -
- )
)
∵ <
<
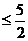 ,∴
,∴ +
+ <5,
<5, -
- <0,
<0,
∴ -
- >0,即
>0,即  >
>  ..
..
∴ =
= -5
-5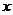 +6在(-
+6在(- ,
, ]上是减函数.
]上是减函数.
类似地,可以证明 在[
在[ ,+
,+ )上是增函数.
)上是增函数.
⑵ =-
=- +9的图象是以(0,9)为顶点、
+9的图象是以(0,9)为顶点、 轴为对称轴、开口向下的一条抛物线(如图);它的单调区间是(-
轴为对称轴、开口向下的一条抛物线(如图);它的单调区间是(- ,0]与[0,+
,0]与[0,+ ),它在(-
),它在(- ,0]上是增函数,在[0,+
,0]上是增函数,在[0,+ )上是减函数.
)上是减函数.
证明:设 <
<
 0,则
0,则 -
- =-
=-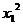 +
+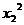 =(
=( +
+ ) (
) ( -
- )
)
∵ <
<
 0,∴
0,∴ +
+ <0,
<0, -
- >0,
>0,
∴ -
- <0,即
<0,即 <
<
.∴ =9-
=9- 在(-
在(- ,0]上是增函数.
,0]上是增函数.
类似地,可以证明 在[0,+
在[0,+ )上是减函数.
)上是减函数.
⒉根据定义证明函数单调性的一般步骤是:⑴设 ,
, 是给定区间内的任意两个值,且
是给定区间内的任意两个值,且 <
< ;⑵作差
;⑵作差 -
- ,并将此差式变形(要注意变形的程度);⑶判断
,并将此差式变形(要注意变形的程度);⑶判断 -
- 的正负(要注意说理的充分性);⑷根据
的正负(要注意说理的充分性);⑷根据 -
- 的符号确定其增减性.
的符号确定其增减性.
答案: 的单调区间有[-2,-1],[-1,0],[0,1],[1,2];
的单调区间有[-2,-1],[-1,0],[0,1],[1,2]; 在区间[-2,-1],[0,1]上是增函数,在区间[-1,0],[1,2]上是减函数.
在区间[-2,-1],[0,1]上是增函数,在区间[-1,0],[1,2]上是减函数.
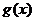 的单调区间有[-
的单调区间有[-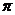 ,-
,- ],[-
],[- ,
, ],[
],[ ,
, 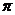 ];
];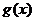 在区间[-
在区间[-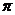 ,-
,- ],[
],[ ,
,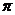 ]上是减函数,在区间[-
]上是减函数,在区间[- ,
, ]上是增函数.
]上是增函数.
说明:要了解函数在某一区间是否具有单调性,从图象上进行观察是一种常用而又较为粗略的方法,严格地说,它需要根据增(减)函数的定义进行证明,下面举例说明.
2判断函数 在R上是增函数还是减函数?并证明你的结论.
在R上是增函数还是减函数?并证明你的结论.
解:设 ,
, ∈R,且
∈R,且 <
< ,
,
∵ -
- =(-3
=(-3 +2)-(-3
+2)-(-3 +2)=3(
+2)=3( -
- ),
),
又 <
< ,∴
,∴ -
- >0,即
>0,即  >
>  .
.
∴ 在R上是减函数.
在R上是减函数.
3判断函数 =
= 在(-
在(- ,0)上是增函数还是减函数并证明你的结论.
,0)上是增函数还是减函数并证明你的结论.
解:设 ,
, ∈(-
∈(- ,0),且
,0),且 <
< ,
,
∵ -
- =
= -
- =
= =
= ,
,
由 ,
, ∈(-
∈(- ,0),得
,0),得
 >0,
>0,
又由 <
< ,得
,得 -
- >0 ,于是
>0 ,于是 -
- >0,即
>0,即  >
>  .
.
∴ =
=  在(0,+
在(0,+  )上是减函数.
)上是减函数.
能否说函数 =
=  在(-
在(- ,+
,+ )上是减函数?
)上是减函数?
答:不能. 因为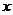 =0不属于
=0不属于 =
=  的定义域.
的定义域.
说明:通过观察图象,对函数是否具有某种性质,作出猜想,然后通过推理的办法,证明这种猜想的正确性,是发现和解决问题的一种常用数学方法.
4 ⑴ 判断函数 在R上的单调性,并说明理由.
在R上的单调性,并说明理由.
⑵ 课本P60练习:4.
解:⑴设 ,
, ∈R,且
∈R,且 <
< ,
,
则 -
- =(k
=(k +b)-(k
+b)-(k +b)=k(
+b)=k( -
- ).
).
若k>0,又 <
< ,∴
,∴ -
- <0,即
<0,即  <
<
.∴ 在R上是增函数.
在R上是增函数.
若k<0,又 <
< ,∴
,∴ -
- >0,即
>0,即  >
>  .
.
∴ 在R上是减函数.
在R上是减函数.
⑵设 ,
, ∈(0,+
∈(0,+ ),且
),且 <
< ,
,
∵ -
- =(
=(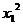 +1)-(
+1)-(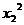 +1)=
+1)= 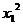 -
-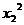 =(
=( +
+ ) (
) ( -
- )
)
∵0< <
< ,∴
,∴ +
+ >0,
>0, -
- <0,
<0,
∴ -
- <0,即
<0,即 <
< ,
,
∴ =
= +1在(0,+
+1在(0,+ )上是增函数.
)上是增函数.
 例1 如图6是定义在闭区间[-5,5]上的函数
例1 如图6是定义在闭区间[-5,5]上的函数 的图象,根据图象说出
的图象,根据图象说出 的单调区间,以及在每一单调区间上,函数
的单调区间,以及在每一单调区间上,函数 是增函数还是减函数.
是增函数还是减函数.
解:函数 的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中
的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中 在区间[-5,-2),[1,3)上是减函数,在区间[-2,1),[3,5]上是增函数.
在区间[-5,-2),[1,3)上是减函数,在区间[-2,1),[3,5]上是增函数.
说明:函数的单调性是对某个区间而言的,对于单独的一点,由于它的函数值是唯一确定的常数,因而没有增减变化,所以不存在单调性问题;另外,中学阶段研究的主要是连续函数或分段连续函数,对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也就单调,因此,在考虑它的单调区间时,包括不包括端点都可以;还要注意,对于在某些点上不连续的函数,单调区间不包括不连续点.
例2 证明函数 在R上是增函数.
在R上是增函数.
证明:设 是R上的任意两个实数,且
是R上的任意两个实数,且 <
< ,则
,则
 -
- =(3
=(3 +2)-(3
+2)-(3 +2)=3(
+2)=3( -
- ),
),
由 <
< x,得
x,得 -
- <0 ,于是
<0 ,于是 -
- <0,即
<0,即  <
< .
.
∴ 在R上是增函数.
在R上是增函数.
例3 证明函数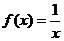 在(0,+
在(0,+ )上是减函数.
)上是减函数.
证明:设 ,
, 是(0,+
是(0,+ )上的任意两个实数,且
)上的任意两个实数,且 <
< ,
,
则 -
- =
= -
- =
= ,
,
由 ,
, ∈(0,+
∈(0,+  ),得
),得
 >0,
>0,
又由 <
< ,得
,得 -
- >0 ,于是
>0 ,于是 -
- >0,即
>0,即 >
> 
∴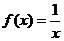 在(0,+
在(0,+  )上是减函数.
)上是减函数.
例4.讨论函数 在(-2,2)内的单调性.
在(-2,2)内的单调性.
解:∵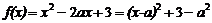 ,对称轴
,对称轴
∴若 ,则
,则 在(-2,2)内是增函数;
在(-2,2)内是增函数;
若 则
则 在(-2,a)内是减函数,在[a,2]内是增函数
在(-2,a)内是减函数,在[a,2]内是增函数
若 ,则
,则 在(-2,2)内是减函数.
在(-2,2)内是减函数.
⒈ 增函数与减函数
定义:对于函数 的定义域I内某个区间上的任意两个自变量的值
的定义域I内某个区间上的任意两个自变量的值 ,⑴若当
,⑴若当 <
< 时,都有
时,都有 <
< ,则说
,则说 在这个区间上是增函数(如图3);⑵若当
在这个区间上是增函数(如图3);⑵若当 <
< 时,都有
时,都有 >
> ,则说
,则说 在这个区间上是减函数(如图4).
在这个区间上是减函数(如图4).
说明:函数是增函数还是减函数,是对定义域内某个区间而言的.有的函数在一些区间上是增函数,而在另一些区间上不是增函数.例如函数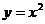 (图1),当
(图1),当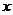 ∈[0,+
∈[0,+ )时是增函数,当
)时是增函数,当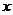 ∈(-
∈(- ,0)时是减函数.
,0)时是减函数.
⒉ 单调性与单调区间
若函数y=f(x)在某个区间是增函数或减函数,则就说函数 在这一区间具有(严格的)单调性,这一区间叫做函数
在这一区间具有(严格的)单调性,这一区间叫做函数 的单调区间.此时也说函数是这一区间上的单调函数.
的单调区间.此时也说函数是这一区间上的单调函数.
在单调区间上,增函数的图象是上升的,减函数的图象是下降的.
 说明:⑴函数的单调区间是其定义域的子集;
说明:⑴函数的单调区间是其定义域的子集;
⑵应是该区间内任意的两个实数,忽略需要任意取值这个条件,就不能保证函数是增函数(或减函数),例如,图5中,在 那样的特定位置上,虽然使得
那样的特定位置上,虽然使得 >
> ,但显然此图象表示的函数不是一个单调函数;
,但显然此图象表示的函数不是一个单调函数;
⑶除了严格单调函数外,还有不严格单调函数,它的定义类似上述的定义,只要将上述定义中的“ <
< 或
或 >
> , ”改为“
, ”改为“

 或
或

 ,”即可;
,”即可;
⑷定义的内涵与外延:
内涵是用自变量的大小变化来刻划函数值的变化情况;
外延①一般规律:自变量的变化与函数值的变化一致时是单调递增,自变量的变化与函数值的变化相对时是单调递减.
②几何特征:在自变量取值区间上,若单调函数的图象上升,则为增函数,图象下降则为减函数.
⒈ 复习:我们在初中已经学习了函数图象的画法.为了研究函数的性质,我们按照列表、描点、连线等步骤先分别画函数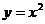 和
和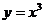 的图象.
的图象. 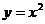 的
的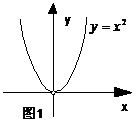
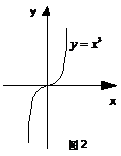 图象如图1,
图象如图1,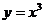 的图象如图2.
的图象如图2.
⒉ 引入:从函数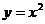 的图象(图1)看到:
的图象(图1)看到:
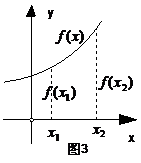 图象在
图象在 轴的右侧部分是上升的,也就是说,当
轴的右侧部分是上升的,也就是说,当 在区间[0,+
在区间[0,+ )上取值时,随着
)上取值时,随着 的增大,相应的
的增大,相应的 值也随着增大,即如果取
值也随着增大,即如果取 ∈[0,+
∈[0,+ ),得到
),得到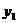 =
= ,
, =
= ,那么当
,那么当 <
< 时,有
时,有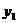 <
< .
.
这时我们就说函数 =
= =
= 在[0,+
在[0,+  )上是增函数.
)上是增函数.
图象在 轴的左侧部分是下降的,也就是说,
轴的左侧部分是下降的,也就是说,
当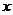 在区间(-
在区间(- ,0)上取值时,随着
,0)上取值时,随着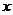 的增大,
的增大,
 相应的
相应的 值反而随着减小,即如果取
值反而随着减小,即如果取 ∈(-
∈(- ,0),得到
,0),得到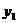 =
= ,
, =
= ,那么当
,那么当 <
< 时,有
时,有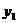 >
> .
.
这时我们就说函数 =
= =
= 在(-
在(- ,0)上是减函数.
,0)上是减函数.
函数的这两个性质,就是今天我们要学习讨论的.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com