2、位置、位移和路程

⑴位置：质点在空间所处的确定的点，可用坐标来表示。

⑵位移：描述质点位置改变的物理量，是矢量。方向由初位置指向末位置。大小则是从初位置到末位置的直线距离

⑶路程：质点实际运动轨迹的长度，是标量。只有在单方向的直线运动中，位移的大小才等于路程。

1、质点：

⑴定义：用来代替物体的只有质量、没有形状和大小的点，它是一个理想化的物理模型。

⑵物体简化为质点的条件：只考虑平动或物体的形状大小在所研究的问题中可以忽略不计这两种情况。

4、简谐运动的图象

⑴简谐运动图象：简谐运动的位移-时间图象通常称为振动图象，也叫振动曲线。

⑵简谐运动振动图象的特点所有简谐运动的振动图象都是正弦或余弦曲线。

(3)简谐运动图象的物理意义表示振动物体相对于平衡位置的位移随时间的变化情况，或反映位移随时间的变化规律。振动图象描述的是一个振动质点在各个不同时刻相对于平衡位置的位移，不是反映质点的运动轨迹。

⑷简谐运动振动图象的应用

①判断振动的性质

②读出振动的振幅A

③读出任意时刻t对平衡位置的位移

④读出振动的周期T

⑤判断任意时刻回复力和加速度的方向

⑥任意时刻的速度方向

⑦图象随时间的变化

例题：某物体始终在做简谐运动，某时刻开始计时，得到的振动图象如图所示，则：

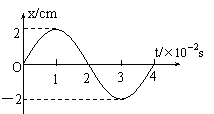①该振动的振幅是_______，周期是________。

②若振动所在的直线向右规定为离开平衡位置位移的正方向，那么1.5×10^－2 s时刻的物体的运动方向是________，加速度的方向是_________。

③物体在2.5×10^－2s时刻，动能正在_______，动量的大小正在_______(填“增大”或“减小”)

④计时开始前2×10^－2s时刻，物体的位移大小为_______，速度方向_______，加速度大小________。

⑤0-10×10^－2s时间内物体还有_____次与零时刻的速度相同(即运动状态相同)。

⑥0-10×10^－2s时间内物体共有_____次速度与1.5×10^－2s时刻的速度相同。

⑦若将1×10^－2s时刻取做零时刻，并将原来规定的正方向规定为负方向，画出振动的图象。

3、振幅、周期和频率　　 　

⑴振幅

①物理意义：振幅是描述振动强弱的物理量。

　　 ②定义：振动物体离开平衡位置的最大距离，叫做振动的振幅。

③单位：在国际单位制中，振幅的单位是米(m)。

④振幅和位移的区别

①振幅是指振动物体离开平衡位置的最大距离；而位移是振动物体所在位置与平衡位置之间的距离。

②对于一个给定的振动，振子的位移是时刻变化的，但振幅是不变的③学生代表答：

③位移是矢量，振幅是标量。

④振幅等于最大位移的数值。　

⑵周期和频率

①全振动

振动物体以相同的速度相继通过同一位置所经历的过程，也就是连续的两次位置和振动状态都相同时所经历的过程，叫做一次全振动。

②周期和频率

a、周期：做简谐运动的物体完成一次全振动所需的时间，叫做振动的周期，单位：s。

b、频率：单位时间内完成的全振动的次数，叫频率，单位：Hz，1Hz＝1 s^－1。

c、周期和频率之间的关系：

T＝

d、研究弹簧振子的周期

弹簧振子的周期由振动系统本身的质量和劲度系数决定，质量较小时周期较小，劲度系数较大时周期较小。周期与振幅无关。

e、固有周期和固有频率

对一个确定的振动系统，振动的周期和频率只与振动系统本身有关，所以把周期和频率叫做固有周期和固有频率。

例题：如图所示，质量为m的小球放在劲度为k的轻弹簧上，使小球上下振动而又始终未脱离弹簧。⑴最大振幅A是多大？⑵在这个振幅下弹簧对小球的最大弹力F_m是多大？

解析：该振动的回复力是弹簧弹力和重力的合力。在平衡位置弹力和重力等大反向，合力为零；在平衡位置以下，弹力大于重力，F- mg=ma，越往下弹力越大；在平衡位置以上，弹力小于重力，mg-F=ma，越往上弹力越小。平衡位置和振动的振幅大小无关。因此振幅越大，在最高点处小球所受的弹力越小。极端情况是在最高点处小球刚好未离开弹簧，弹力为零，合力就是重力。这时弹簧恰好为原长。

⑴最大振幅应满足kA=mg,　 A=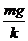

⑵小球在最高点和最低点所受回复力大小相同，所以有：F_m-mg=mg，F_m=2mg

例题：一弹簧振子做简谐运动，周期为T，下面说法正确的是(　　　 )

A．若t时刻和(t+△t)时刻振子运动位移的大小相等、方向相同，别△T一定等于T的整数倍

B．若t时刻和(t+△t)时刻振子运动速度的大小相等、方向相反，则△t一定等于的整数倍

C．若△t=T，则在t时刻和 (t+△t)时刻振子运动的加速度一定相等　　 。-

D．若△t=，则在t时刻和(t+△t)时刻弹簧的长度一定相等

解析：如图为某一物体的振动图线，对 A选项图中的B、C两点的振动位移的大小、方向相同，但△t≠T ，A错． B、C两点速度大小相同，方向相反，△t≠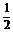T，故A、B均不对．对C选项，因为△t=T，所以t和t +△t时刻振子的位移 、速度、加速度等都将周期性重复变化，加速度相同，C对．对D选　 ，△t=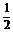 T ，振子位移大小相同方向相反，弹簧的形变相同，但弹簧的长度不一定相同，D错．

2、简谐运动

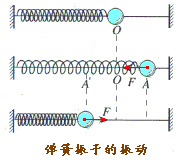
(1)弹簧振子：一个轻质弹簧联接一个质点，弹簧的另一端固定，就构成了一个弹簧振子。

(2)振动形成的原因

①回复力：振动物体受到的总能使振动物体回到平衡位置，且始终指向平衡位置的力，叫回复力。

振动物体的平衡位置也可说成是振动物体振动时受到的回复力为零的位置。

②形成原因：振子离开平衡位置后，回复力的作用使振了回到平衡位置，振子的惯性使振子离开平衡位置；系统的阻力足够小。

(3)振动过程分析

(4)简谐运动的力学特征

①简谐运动：物体在跟偏离平衡位置的位移大小成正比，并且总指向平衡位置的回复力的作用下的振动，叫做简谐运动。

②动力学特征：回复力F与位移x之间的关系为

F＝－kx

式中F为回复力，x为偏离平衡位置的位移，k是常数。简谐运动的动力学特征是判断物体是否为简谐运动的依据。

③简谐运动的运动学特征

a＝－ x

加速度的大小与振动物体相对平衡位置的位移成正比，方向始终与位移方向相反，总指向平衡位置。

简谐运动加速度的大小和方向都在变化，是一种变加速运动。简谐运动的运动学特征也可用来判断物体是否为简谐运动。

例题：试证明在竖直方向的弹簧振子做的也是简谐振运动。

证明：设O为振子的平衡位置，向下方向为正方向，此时弹簧形变量为x₀，根据胡克定律得

x₀＝mg/k

当振子向下偏离平衡位置x时，回复力为

F＝mg－k(x+x₀)

则F＝－kx

所以此振动为简谐运动。

1、机械振动

(1)平衡位置：物体振动时的中心位置，振动物体未开始振动时相对于参考系静止的位置，或沿振动方向所受合力等于零时所处的位置叫平衡位置。

(2)机械振动：物体在平衡位置附近所做的往复运动，叫做机械振动，通常简称为振动。

(3)振动特点：振动是一种往复运动，具有周期性和重复性

4、往往是一道题中要求几个量，所以更多的情况是整体法和隔离法同时并用，这比单纯用隔离法要简便。

⑹牛顿定律应用中临界的问题

　如果物体的受力情况(包括受力的个数、某个力的性质)或运动情况发生突然变化时，物体所处的状态称为临界态，它是两种不同状态共存的衔接。物体处于临界态必须满足的条件就是所谓的临界条件。

　一般在题中出现“刚好”、“恰好”、“最大”、“最小”时都有相应的临界条件。解题时要特别注意把握住，通常采用极限分析法(即将变化因素推至两个极端)来使临界条件凸现出来，这往往是解这类的关键。　　

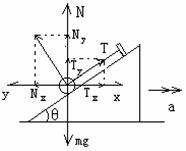
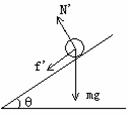
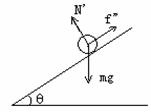
例题：在倾角为q的光滑斜面体上，放有质量为m的小球，小球用一根平行斜面的细线系在斜面上端。如右图所示。当斜面体向右作加速度为a的匀加速直线运动时，求线对小球的拉力和斜面对小球的弹力。

　　　 解析：如右图所示，小球受三个力：重力mg、弹力N、拉力T。因为小球具有水平向右的加速度a，所以取水平方向和竖直方向建立坐标，并将N和T做正交分解，根据牛顿第二定律列出分量方程：

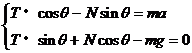
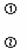
‚两式联立，经数学处理，解得：

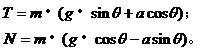
从上述计算结果可以看出：当加速度a越大时，线上拉力T越大，弹力N越小；当加速度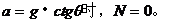

　　　 小结：当研究对象所受的各个外力不在一个方向上时，解题时通常采用正交分解法。

　　　 两个正交方向，即坐标轴的方向，原则上是可以任意选取的，但如果选取适当，就可以使需要分解的力达到最小个数，在列方程和计算时就显得简便。因此，在动力学的正交分解中，常取正交方向的一个方向(如x方向)与加速度a的方向一致，则正交方向中的另一个方向(如y方向)上就没有加速度，故所列分量方程：

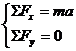
　　　 由于加速度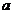也是矢量，有些情况是在将外力作正交分解的同时，也需要将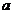作正交分解，这时的分量方程为：

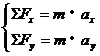
例题：在光滑的水平轨道上有两个半径都是r的小球A和B，质量分别为m和2m，当两球心间距离大于l(l比2r大得多)时，两球之间无相互作用力；当两球心间的距离等于或小于l时，两球间存在相互作用的恒定斥力F，设A球从远离B球处以速度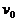沿两球连心线向原来静止的B球运动，如右图所示，欲使两球不发生接触，必须满足的条件？

　　　 解析：A球开始做匀速直线运动，直到与B球接近至l时，开始受到与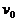反向的恒力而做匀减速直线运动。B球则从A与其相近至l开始，受到与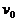同方向的恒力，做初速度为零的匀加速直线运动。两球间距离逐渐变小。

　　　 两球不发生接触的临界条件是：两球速度相等时，两球间的距离最小，且此距离必须大于2r。即

　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ------

　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ------‚

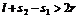其中为两球间距离从 l变到最小的过程中A、B两球通过的路程。

　　　 由牛顿第二定律可得，A球在减速运动，B球在加速运动的过程中，A、B两球的加速度大小为：

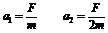
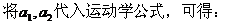
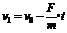　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ------ƒ

　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ------„

　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ------…

　　　　　　　 　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ------†

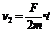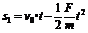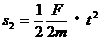上述6式联立解得

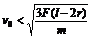
　　　 小结：对于较为复杂的物理问题，应建立好物理情景，进而找到物理过程之间的联系或临界条件，问题才能迎刃而解。

例题：斜面长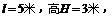底端有一个质量为5千克的物体A，它和斜面间的摩擦系数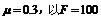牛顿的水平推力推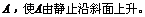在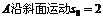米后撤去力F，问由撤力时算起再经多少时间A回到底端？

　　　 解析：因为A在各段运动过程中，受力的情况是不一样的， 所以，解此题必须分段计算。

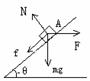
　　　 第一段，A和F作用下沿斜面匀加速上升，将A受的力(如右图所示)，正交分解到平行于斜面和垂直于斜面两个方向上去。

　　　 根据牛顿第二定律列方程：

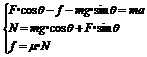
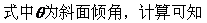
代入前式，可得A沿斜面向上的加速度：

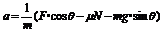
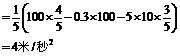
因此，撤力时A的速度为：

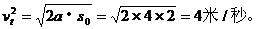
　　　 第二段，撤力后，因为A已经有了一定的速度，所以A应做沿斜面匀减速上升，但因撤去F使A对斜面的压力发生了变化，所以摩擦力的值也应随之改变。对A进行受力分析，如右图所示，列方程组可求得加速度a¢。

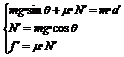
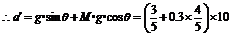
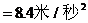
　　　 A由撤力到升至最高点时间t₂满足：

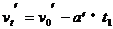
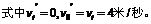
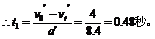
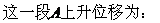
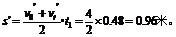
　　　 第三段，A从最高点匀加速沿斜面下滑，摩擦力的方向应变为沿斜面向上。A受力如右图所示，根据牛顿第二定律可求下滑加速度a²：

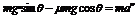
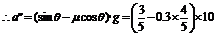
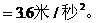
　　　 A从最高点滑到底端的位移为

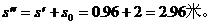
　　　 由公式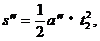可求这段位移所需时间

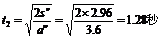
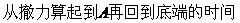
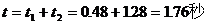
　　　 小结：有关牛顿运动定律应用的问题，常见以下两种类型：(1)已知物体受力情况，求物体的运动情况(如位移、时间、速度等)。(2)已知物体的运动情况，求物体受力情况。但不管哪种类型，一般都应先由已知条件求出加速度，然后再由此求解。

　　　 解题的一般步骤是：(1)理解题意，弄清物理图景和物理过程；(2)恰当选取研究对象；(3)分析它的受力情况，画出被研究对象的受力图。对于各阶段运动中受力不同的物体，必须分段分析计算；(4)按国际单位制统一各个物理量的单位；(5)根据牛顿运动定律和运动学规律建立方程求解。

3、用整体法解题时，必须满足一个条件，即连结体各部分加速度的值是相同的。如果不是这样，便只能用隔离法求解。

2、只要有可能，要尽量运用整体法。因为整体法的好处是，各隔离体之间的许多未知力，都作为内力而不出现在牛顿第二定律方程式中，对整体列一个方程即可。

1、当用隔离法时，必须按题目的需要进行恰当的选择隔离体，否则将增加运算过程的繁琐程度。