2、宇宙速度

　⑴卫星的绕行速度v

　由得：(式中M为地球的质量，m为人造卫星的质量，r为卫星运行的轨道半径)

　①卫星与地心的距离r越大，则v越小

当r最小时，r＝R时，线速度最大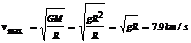　(第一宇宙速度7.9km/s)

②高轨道发射卫星比低轨道发射卫星困难。原因是高轨道发射卫星时火箭要克服地球对它引力做更多的功

⑵三种宇宙速度

　①第一宇宙速度(环绕速度)：v₁=7.9km/s

　　a、意义：它是人造卫星在地面附近绕地球做匀速圆周运动所必须具备的速度

b推导：方法一：由得：　

方法二：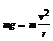　　

c、如果卫星的速度小于第一宇宙速度，卫星将落到地面而不能绕地球运转；等于这个速度卫星刚好能在地球表面附近作匀速圆周运动；如果大于7.9km/s，而小于11.2km/s，卫星将沿椭圆轨道绕地球运行，地心就成为椭圆轨道的一个焦点。

②第二宇宙速度(脱离速度)：

a、意义：使卫星挣脱地球的引力束缚，成为绕太阳运行的人造行星的最小发射速度。

b、如果人造天体的速度大于11.2km/s而小于16.7km/s，则它运行的轨道相对于太阳是椭圆，太阳就成为该椭圆轨道的一个焦点。

③第三宇宙速度(逃逸速度)：v₃＝16.7km/s

a、意义：使卫星挣脱太阳引力束缚的最小发射速度

b、如果人造天体具有这样的速度并沿着地球绕太阳的的公转方向发射时，就可以摆脱地球和太阳的引力的束缚而遨游太空了。

例题：已知物体从地球上的逃逸速度(第二宇宙速度)v₂=，其中G、M_E、R_E分别是引力常量、地球的质量和半径，已知G=6.67×10^-11N·m²/kg²，c=2.9979×10⁸m/s求下列问题：(1)逃逸的速度大于真空中光速的天体叫做黑洞，设某黑洞的质量等于太阳的质量M=1.98×10³⁰kg，求它的可能最大半径(这个半径叫Schwarzchild半径)；(2)在目前天文观测范围内，物质的平均密度为10^-27kg/m³，如果认为我们的宇宙是这样一个均匀大球体，其密度使得它的逃逸速度大于光在真空中的速度c，因此任何物体都不能脱离宇宙，问宇宙的半径至少多大？

解析：(1)由题目提供的信息可知，任何天体均存在其所对应的逃逸速度v₂= 　，其中M、R为天体的质量和半径，对黑洞模型来说v₂>c，所以R<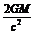==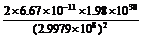2.94×10³m,即质量为1.98×10³⁰kg的黑洞的最大半径为2.94×10³m.。

(2)把宇宙视为一普通天体，则其质量为M=ρ·V=ρ·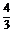πR³

其中R为宇宙的半径，ρ为宇宙的密度，则宇宙所对应的逃逸速度为v₂=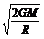，由于宇宙密度使得逃逸速度大于光速c即，v₂>c

则由以上三式可得R>=4.01×10²⁶m，合4.24×10¹⁰光年。

点评： 这是一道假设推理题，要求建立一个物理假象的模型，这能培养学生的想象力和处理解决问题的能力，同时这也是高考趋势的发展方向。《考试说明》要求考生：能够根据已知的知识和所给的物理事实、条件，对物理问题进行逻辑推理和论证，得出正确的结论或作出正确的判断，并能把推理过程表达出来，论证推理有助于加强对学生的推理能力的考查。

2、万有引力定律：

⑴表述：自然界中任何两个物体都是相互吸引的，引力的大小跟这两个物体的质量的乘积成正比，跟它们的距离的二次方成反比

⑵公式：　其中M₁、M₂是两个物体的质量，r为两物体间的距离，G为万有引力常量

⑶引力常量G：①适用于任何两个物体　

②意义：它在数值上等于两个质量都是1㎏的物体相距1m时的相互作用力

③G的通常取值为G＝6.67×10^－11Nm²/㎏²

⑷适用条件：①万有引力定律只适用于质点间引力大小的计算。当两物体间的距离远远大于每个物体的尺寸时物体可以看成质点，直接用万有引力定律计算

②当两物体是质量分布均匀的球体时，它们间的万有引力也可直接用公式计算，但式中的r是指两球心间的距离

③当研究物体不能看成质点时，可以把物体假想分割成无数个质点，求出每个质点与另一个物体的所有质点的万有引力，然后求合力。

　⑸地球上质量为m的物体所受的重力近似等于地球对物体的万有引力，可用mg＝GMm/r²计算

　⑹对万有引力定律的进一步理解

　①普遍性：万有引力是普遍存在于宇宙中的任何有质量的物体间的相互吸引力，它是自然界的物体间的基本相互作用之一。

②相互性：两个物体相互作用的引力是一对作用力与反作用力，符合牛顿第三定律

③宏观性：通常情况下，万有引力非常小，只有在质量巨大的天体间或天体与物体间它的存在才有宏观的物理意义。在微观世界中，粒子的质量都非常小，粒子间的万有引力很不显著，万有引力可忽略不计

⑺引力常量G的测定：

　①卡文迪许扭秤实验：

②G的值：利用控制变量法多次进行测量，得出万有引力常量G＝6.67259×10^－11Nm²/kg²，

通常取6.67×10^-11 Nm²/kg²。

　③测定引力常量的意义:证明了万有引力的存在；使得万有引力定律有了真正的实用价值，可测定远离地球的一些天体的质量、平均密度等。如根据地球表面的重力加速度可以测定地球的质量

1、开普勒三定律：

⑴开普勒第一定律(轨道定律)：所有的行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上

⑵开普勒第二定律(面积定律)：太阳和行星的连线在相等的时间内扫过相等的面积

⑶开普勒第三定律(周期定律)：所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等

　对T₁、T₂表示两个行星的公转周期，R₁、R₂表示两行星椭圆轨道的半长轴，则周期定律可表示为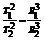

或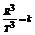，比值k是与行星无关而只与太阳有关的恒量

[注意]：⑴开普勒定律不仅适用于行星，也适用于卫星，只不过此时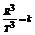^‘，比值k^’是由行星的质量所决定的另一恒量。

　　　　 ⑵行星的轨道都跟圆近似，因此计算时可以认为行星是做匀速圆周运动

　　　　　 ⑶开普勒定律是总结行星运动的观察结果而总结归纳出来的规律，它们每一条都是经验定律，都是从观察行星运动所取得的资料中总结出来的。

例题：飞船沿半径为R的圆周绕地球运动，其周期为T，如果飞船要返回地面，可在轨道上的某一点A处，将速率降低到适当数值，从而使飞船沿着以地心为焦点的椭圆轨道运动，椭圆和地球表面在B点相切，如图所示，如果地球半径为R₀，求飞船由A点到B点所需要的时间。

解析：依开普勒第三定律知，飞船绕地球做圆周(半长轴和半短轴相等的特殊椭圆)运动时，其轨道半径的三次方跟周期的平方的比值，等于飞船绕地球沿椭圆轨道运动时，其半长轴的三次方跟周期平方和比值，飞船椭圆轨道的半长轴为，设飞船沿椭圆轨道运动的周期为T＇，则有

而飞船从A点到B点所需的时间为

t=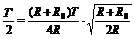

2、若上题中，看不到明暗条纹，只看到一片亮区，应注意如何调节？

　[解析]这是由于单缝与双缝不平行所致，可用遮光筒上的调节杆拨动单缝，直到看到清晰的明暗条纹为止。

5、调节的基本依据是：照在像屏上的光很弱，主要原因是灯丝与单缝、双缝、测量头与遮光筒不共轴线所致，干涉条纹不清晰一般主要原因是单缝与双缝不平行所致。

[例题] 1、某位同学在测定光波的波长实验中，透过测量头的目镜观察双缝干涉图样时，发现，只在工左侧视野中有明暗相间的条纹出现，而右侧没有，应如调节？

　[解析]这是由于测量头目镜偏离遮光筒轴线所致，可以转动测量头上的手轮，使测量头向左移动，直到在目镜中看到明暗条纹布满视野为止。

4、光源灯丝最好为线状灯丝，并与单缝平行靠近。

3、安装时，注意调节光源、滤光片、单缝、双缝的中心均在遮光筒的中心轴线上，并使单缝、双缝平行且竖直

2、滤光片、单缝、双缝、目镜等如有灰尘，应用擦镜纸轻轻擦去。

1、双缝干涉仪是比较精密的仪器。应轻拿轻放，不要随便拆解遮光筒，测量头等元件。