
5.相互作用中的动量与能量,三类碰撞中能量的变化:
(1)完全非弹性碰撞:动量守恒,机械能损失最大
(2)完全弹性碰撞:动量守恒,机械能也守恒。
设两物体发生完全弹性碰撞,其中m1以v1匀速运动,m2静止。
据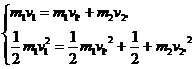
可得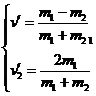
讨论:(a)当m1>m2时,v1′与v1方向一致;
(b)当m1=m2时,v1′=0,v2′=v1,即m1与m2交换速度
(c)当m1<m2时,v1′反向,v2′与v1同向。
(3)非完全弹性碰撞:为一般情况,只有动量守恒,机械能有损失,损失量不最大,亦不最小。
4.动能定理与能量守恒定律关系--理解“摩擦生热”(Q=f·Δs)
设质量为m2的板在光滑水平面上以速度υ2运动,质量为m1的物块以速度υ1在板上同向运动,且υ1>υ2,它们之间相互作用的滑动摩擦力大小为f,经过一段时间,物块的位移为s1,板的位移s2,此时两物体的速度变为υ′1和υ′2由动能定理得:
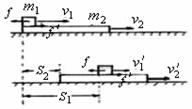 -fs1=
-fs1= m1υ1′2/2-m1υ12/2 ①
m1υ1′2/2-m1υ12/2 ①
fs2=m2υ2′2/2-m2υ22/2 ②
在这个过程中,通过滑动摩擦力做功,机械能不断转化为内能,即不断“生热”,由能量守恒定律及①②式可得:
Q=(m1υ12/2+m2υ22/2)-(m1υ1′2/2-m2υ2′2/2)=f(s1-s2)= f·Δs ③
由此可见,在两物体相互摩擦的过程中,损失的机械能(“生热”)等于摩擦力与相对位移的乘积。
特别要指出,在用Q= f·Δs 计算摩擦生热时,正确理解是关键。这里分两种情况:
(1)若一个物体相对于另一个物体作单向运动,Δs为相对位移;
(2)若一个物体相对于另一个物体作往返运动,Δs为相对路程。
3.动量守恒定律与动量定理的关系
动量守恒定律的数学表达式为:m1v1+m2v2=m1v1′+m2v2′,可由动量定理推导得出.
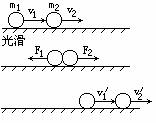 如图所示,分别以m1和m2为研究对象,根据动量定理:
如图所示,分别以m1和m2为研究对象,根据动量定理:
F1Δt= m1v1′- m1v1 ①
F2Δt= m2v2′- m2v2 ②
F1=-F2 ③
∴ m1v1+m2v2=m1v1′+m2v2′
可见,动量守恒定律数学表达式是动量定理的综合解.动量定理可以解决动量守恒问题,只是较麻烦一些.因此,不能将这两个物理规律孤立起来.
2.两个“定律”
(1)动量守恒定律:适用条件--系统不受外力或所受外力之和为零
公式:m1v1+m2v2=m1v1′+m2v2 ′或 p=p ′
(2)机械能守恒定律:适用条件--只有重力(或弹簧的弹力)做功
公式:Ek2+Ep2=Ek1+Ep1 或 ΔEp= -ΔEk
1.两个“定理”
(1)动量定理:F·t=Δp 矢量式 (力F在时间t上积累,影响物体的动量p)
(2)动能定理:F·s=ΔEk 标量式 (力F在空间s上积累,影响物体的动能Ek)
 动量定理与动能定理一样,都是以单个物体为研究对象.但所描述的物理内容差别极大.动量定理数学表达式:F合·t=Δp,是描述力的时间积累作用效果--使动量变化;该式是矢量式,即在冲量方向上产生动量的变化.
动量定理与动能定理一样,都是以单个物体为研究对象.但所描述的物理内容差别极大.动量定理数学表达式:F合·t=Δp,是描述力的时间积累作用效果--使动量变化;该式是矢量式,即在冲量方向上产生动量的变化.
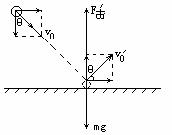
例如,质量为m的小球以速度v0与竖直方向成θ角打在光滑的水平面上,与水平面的接触时间为Δt,弹起时速度大小仍为v0且与竖直方向仍成θ角,如图所示.则在Δt内:
以小球为研究对象,其受力情况如图所示.可见小球所受冲量是在竖直方向上,因此,小球的动量变化只能在竖直方向上.有如下的方程:
F′击·Δt-mgΔt=mv0cosθ-(-mv0cosθ)
小球水平方向上无冲量作用,从图中可见小球水平方向动量不变.
综上所述,在应用动量定理时一定要特别注意其矢量性.应用动能定理时就无需作这方面考虑了.Δt内应用动能定理列方程:W合=mυ02/2-mυ02 /2 =0
1.动量 2.机械能


5、地球的同步卫星(通讯卫星)
⑴同步卫星:相对地面静止,跟地球自转同步的卫星叫做同步卫星。
 ⑵同步卫星的特点:
⑵同步卫星的特点:
①周期等于地球的自转周期T(24小时),且从西向东运转(与地球自转方向相同),角速度大小为
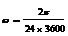 (rad/s)
(rad/s)
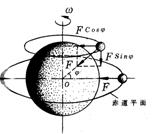
②轨道平面与赤道平面同心――保证万有引力全部用作向心力。如图所示,如果轨道平面在赤道平面正上方(或正下方),卫星将在万有引力垂直地轴分量(Fcosφ)的作用下,绕地轴作圆周运动;同时在平行地轴的分量(Fsinφ)的作用下,在赤道平面上下振动。这样,就不可能与地球同步。
⑶定点高度――距地面h=35800(千米)
在ω一定的条件下,同步卫星的定点高度不具有任意性。根据 
所以定点高度为 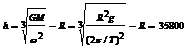 (千米)
(千米)
⑷环绕速度――v=3.08(千米/秒)
在轨道半径一定的条件下,同步卫星的环绕速度也一定,且为
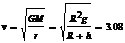 (千米/秒)
(千米/秒)
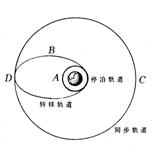 ⑸变轨道发射--发射同步卫星,一般不采用普通卫星的直接发射方法,而是采用变轨道发射(如图)
⑸变轨道发射--发射同步卫星,一般不采用普通卫星的直接发射方法,而是采用变轨道发射(如图)
首先,利用第一级火箭将卫星送到180-200千米的高空,然后依靠惯性进入圆停泊轨道(A)当到达赤道上空时,第二、三级火箭点火,卫星进入位于赤道平面内的椭圆转移轨道(B),且轨道的远地点(D)为35800千米。当到达远地点时,卫星启动发动机,然后改变方向进入同步圆轨道(C)这种发射方法有两个优点:一是对火箭推力要求较低;二是发射场的位置不局限在赤道上。
4、人造卫星的轨道
⑴人造地球卫星的轨道一般为椭圆轨道,地球在其一个焦点上,此时卫星进入地面附近轨道(近地点)时速度v满足:7.9km/s<v<11.2km/s。
在中学阶段,我们将卫星的运行轨道视为圆轨道,此时的绕行速率v满足: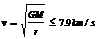
⑵人造地球卫星的轨道平面必通过地球的中心,对于同步卫星,其轨道平面与赤道平面重合。
3、人造卫星的发射速度和运行速度:
⑴发射速度:
所谓发射速度是指被发射物在地面附近离开发射装置时的初速度,并且一旦发射后就再无能量补充,被发射物仅依靠自己的初动能克服地球引力上升一定的高度,进入运动轨道。要发射一颗人造地球卫星,发射速度不能小于第一宇宙速度。若发射速度等于第一宇宙速度,卫星只能“贴着”地面近地运行。如果要使人造卫星在距地面较高的轨道上运行,就必须使发射速度大于第一宇宙速度。
⑵运行速度:是指卫星在进入运行轨道后绕地球做匀速圆周运动的线速度。当卫星“贴着”地面运行时,运行速度等于第一宇宙速度。根据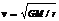 可知,人造卫星距地面越高(即轨道半径r越大),运行速度越小。实际上,由于人造卫星诉轨道半径都大于地球半径,所以卫星的实际运行速度一定小于发射速度。
可知,人造卫星距地面越高(即轨道半径r越大),运行速度越小。实际上,由于人造卫星诉轨道半径都大于地球半径,所以卫星的实际运行速度一定小于发射速度。
⑶人造卫星诉发射速度与运行速度之间的大小关系:11.2km/s>v发射≥7.9km/s>v运行
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com