
3、感应电动势
(1)定义:在电磁感应现象中产生的电动势,叫做感应电动势。从低电势位置指向高电势位置。
(2)产生感应电动势的条件:穿过回路的磁通量发生变化。
(3)物理意义:感应电动势是反映电磁感应现象本质的物理量。
(4)方向规定:内电路中的感应电流方向,为感应电动势方向。

3、电磁感应现象中能量的转化
能的转化守恒定律是自然界普遍规律,同样也适用于电磁感应现象。
2、电磁感应现象
(1)电磁感应现象:利用磁场产生电流的现象,叫做电磁感应现象。
(2)感应电流:在电磁感应现象中产生的电流,叫做感应电流。
(3)产生电磁感应现象的条件
①产生感应电流条件的两种不同表述
a.闭合电路中的一部分导体与磁场发生相对运动
b.穿过闭合电路的磁场发生变化
②两种表述的比较和统一
a.两种情况产生感应电流的根本原因不同
闭合电路中的一部分导体与磁场发生相对运动时,是导体中的自由电子随导体一起运动,受到的洛伦兹力的一个分力使自由电子发生定向移动形成电流,这种情况产生的电流有时称为动生电流。
穿过闭合电路的磁场发生变化时,根据电磁场理论,变化的磁场周围产生电场,电场使导体中的自由电子定向移动形成电流,这种情况产生的电流有时称为感生电流。
b.两种表述的统一
两种表述可统一为穿过闭合电路的磁通量发生变化。
③产生电磁感应现象的条件
不论用什么方法,只要穿过闭合电路的磁通量发生变化,闭合电路中就有电流产生。
条件:a.闭合电路;b.磁通量变化
1、磁通量
设在匀强磁场中有一个与磁场方向垂直的平面,磁场的磁感应强度为B,平面的面积为S,如图所示。
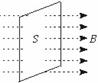
(1)定义:在匀强磁场中,磁感应强B与垂直磁场方向的面积S的乘积,叫做穿过这个面的磁通量,简称磁通。
(2)公式:Φ=BS
当平面与磁场方向不垂直时,如图所示。
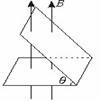
Φ=BS⊥=BScosθ
(3)物理意义
物理学中规定:穿过垂直于磁感应强度方向的单位面积的磁感线条数等于磁感应强度B。所以,穿过某个面的磁感线条数表示穿过这个面的磁通量。
(4)单位:在国际单位制中,磁通量的单位是韦伯,简称韦,符号是Wb。
1Wb=1T·1m2=1V·s。
(5) 磁通密度:B=
磁感应强度B为垂直磁场方向单位面积的磁通量,故又叫磁通密度。
8、 示波管的原理
示波管的原理
(1)构造及作用
①电子枪
发射并加速电子。
②偏转电极
YY':使电子束竖直偏转(加信号电压);
XX':使电子束水平偏转(加扫描电压)。
③荧光屏
④玻璃壳
(2)原理
YY'的作用:被电子枪加速的电子在YY'电场中做匀变速曲线运动,出电场后做匀速直线运动,最后打到荧光屏上。
由y'=(x+)U知,y'与U成正比。
XX'的作用:扫描
加正弦交变电压,显示正弦曲线。
4.用能量观点处理带电粒子在电场中的运动
(1)从功能观点出发分析带电粒子的运动问题时:在对带电粒子受力情况和运动情况进行分析的基础上,再考虑应用恰当的规律解题.如果选用动能定理,要分清有几个力做功,做正功还是做负功,是恒力做功还是变力做功,以及初、末状态的动能.
(2)如果选用能量守恒定律解题时:要分清有多少种形式的能参与转化,哪种形式的能
增加,哪种形式的能减少.并注意电场力做功与路径无关.
3.宏观带电微粒在匀强电场与重力场的复合场中的运动
由于带电微粒在匀强电场中所受电场力与重力都是恒力,因此其处理方法有下列两种:
(1)正交分解法:先将复杂的运动分解为两个互相正交的简单的直线运动,而这两个直线运动的规律我们可以掌握,然后再按运动合成的观点,去求出复杂运动的相关物理量.
(2)等效“重力”法:将重力与电场力进行合成,如图所示,则F等效于“重力”,等效于“重力加速度”,F的方向等效于“重力”的方向.
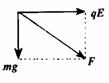
2.微观带电粒子,在电场中或在磁场中时,其重力一律忽略不计,宏观带电微粒,在电场中或在磁场中时,其重力不能忽略.
1、让一价氢离子、一价氦离子和二价氦离子的混合物经过同一加速电场由静止开始加速,然后在同一偏转电场里偏转,不会分成三股。在荧光屏上只出现一个亮点。
7、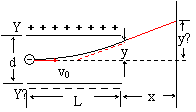 带电粒子的偏转
带电粒子的偏转
如图所示,在真空中水平放置一对金属板Y和Y′,板间距离为d,在两板间加以电压U。现有一质量为m、电荷量为q的带电粒子以水平速度v0射入电场中,求:
(1)带电粒子在电场中的运动及运动方程
带电粒子沿极板方向作速度为v0的匀速运动;
垂直于极板方向作初速度为零的匀加速运动。
粒子的运动类似平抛运动。
以进入点为坐标原点,沿极板方向取x轴,垂直于极板方向取y轴,则粒子在电场中的运动方程为
x=v0t
y=at2=t2
解得:
y=x2 (抛物线轨迹方程)
(2)带电粒子飞过电场的时间
T=
(3)带电粒子离开电场时偏转的侧位移
y=at2==tanφ= (U'为进入偏转电场前的加速电压)
 (4)带电粒子离开电场时的速度大小
(4)带电粒子离开电场时的速度大小
vx=v0
vy=v⊥=aT=
v==
(5)带电粒子离开电场时的偏角
tanφ===U=
φ=arctan(U)
可以证明,将带电粒子的速度方向反向延长后交于极板中线上的中点。
(6)带电粒子射出偏转电场后打到荧光屏上
在距偏转电场粒子射出端为x的地方,有一与极板垂直的荧光屏。带电粒子射出偏转电场后作匀速直线运动,打到荧光屏上。如果在偏转电场中没有加偏转电压,这时带电粒子打在荧光屏的中心点O。设加偏转电压后,粒子打在荧光屏上的点距O点的距离为y',如图所示。
根据相似三角形知识有:
=
y'=(x+)U=tanφ(x+)
例题:一电子在水平偏转电场中,射入时的速度v0=3.0×107m/s。两极板的长度L=6.0cm,相距d=2cm,极板间的电压U=200V。求电子射出电场时竖直偏移的距离y和偏转的角度φ。
解析:电子在竖直方向做匀加速运动,射出电场时竖直偏移的距离为
y=at2==0.36cm
离开电场时的偏转角φ为
tanφ==U
代入数值后得
φ=6.8º
注意:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com