2、嘉兴最初是-------地域形态，后来演变成------，-------，最后演变为------状。是由于----------发展变化造成的。

1、株洲和筑波两个城市呈--------分布。都是沿---------发展的。

15．已知函数y＝f(x)是定义在R上的周期函数，周期T＝5，函数y＝f(x)(－1≤x≤1)是奇函数．又知y＝f(x)在[0,1]上是一次函数，在[1,4]上是二次函数，且在x＝2时函数取得最小值，最小值为－5.

(1)证明：f(1)+f(4)＝0；

(2)试求y＝f(x)，x∈[1,4]的解析式；

(3)试求y＝f(x)在[4,9]上的解析式．

(1)证明：∵y＝f(x)是以5为周期的周期函数，

∴f(4)＝f(4－5)＝f(－1)．

又y＝f(x)(－1≤x≤1)是奇函数，

∴f(1)＝－f(－1)＝－f(4)．

∴f(1)+f(4)＝0.

(2)解：当x∈[1,4]时，由题意，可设

f(x)＝a(x－2)²－5　(a≠0)

由f(1)+f(4)＝0得

a(1－2)²－5+a(4－2)²－5＝0

解得a＝2.

∴f(x)＝2(x－2)²－5　(1≤x≤4)．

(3)解：∵y＝f(x)　(－1≤x≤1)是奇函数，

∴f(0)＝－f(－0)．∴f(0)＝0.

又y＝f(x)　(0≤x≤1)是一次函数，

∴可设f(x)＝kx(0≤x≤1)，

∵f(1)＝2(1－2)²－5＝－3，

又f(1)＝k·1＝k，

∴k＝－3.

∴当0≤x≤1时，f(x)＝－3x；

当－1≤x<0时，0<－x≤1.

∴f(x)＝－f(－x)＝－3x.

∴当－1≤x≤1时，f(x)＝－3x；

当4≤x≤6时，－1≤x－5≤1，

∴f(x)＝f(x－5)＝－3(x－5)＝－3x+15；

当6<x≤9时，1<x－5≤4，

f(x)＝f(x－5)＝2[(x－5)－2]²－5＝2(x－7)²－5.

∴f(x)＝

14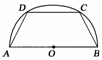．如右图所示，有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，且上底CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域．

解：AB=2R.

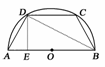C、D在⊙O的半圆周上，

设腰长AD=BC=x，作DE⊥AB，

垂足为E，连接BD，

那么∠ADB是直角，

由此Rt△ADE∽Rt△ABD.

∴AD²=AE×AB，即AE=，

∴CD=AB-2AE=2R-，

所以y=2R+2x+(2R-)，即y=-+2x+4R.

再由，解得0<x<R.

所以y＝－+2x+4R，定义域为(0，R)．

13．已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x²+2x.

(1)求g(x)的解析式；

(2)解不等式g(x)≥f(x)－|x－1|.

解：(1)设函数y＝f(x)的图象上任一点Q(x₀，y₀)关于原点的对称点为P(x，y)，

则　即

∵点Q(x₀，y₀)在函数y＝f(x)的图象上，

∴－y＝x²－2x，即y＝－x²+2x，

故g(x)＝－x²+2x.

(2)由g(x)≥f(x)－|x－1|可得：2x²－|x－1|≤0.

当x≥1时，2x²－x+1≤0，此时不等式无解．

当x<1时，2x²+x－1≤0，∴－1≤x≤.

因此，原不等式的解集为[－1，]．

12.

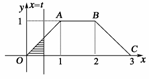
如右图所示．

(1)求对应于折线OABC函数f(x)的解析表达式；

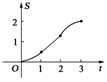
(2)若x=t与折线OABC及x轴所围成(x≤t)的部分面积为S，当t∈[0,3]时，求S与t的函数关系式，并画出图象．

图象如下图所示．

11．(2009·北京海淀区)已知：对于给定的q∈N^*及映射f：A→B，B⊆N^*.若集合C⊆A，且C中所有元素对应的象之和大于或等于q，则称C为集合A的好子集．

①对于q＝2，A＝{a，b，c}，映射f：x→1，x∈A，那么集合A的所有好子集的个数为________；

②对于给定的q，A＝{1,2,3,4,5,6，π}，映射f：A→B的对应关系如下表：

若当且仅当C中含有π和至少A中2个整数或者C中至少含有A中5个整数时，C为集合A的好子集．写出所有满足条件的数组(q，y，z)：________.

答案：4，(5,1,3)

解析：①依题意得集合C中的所有元素的象都是1，且要求C中的所有元素的象之和不小于2，因此集合C中的元素个数可以是2个或3个，满足题意的集合C的个数是C+C＝4.

②依题意知当C中恰好含有A中5个整数时，C为集合A的好子集，因此q≤5；当C中仅含有A中4个整数时，C不是集合A的好子集，因此q>4.又q∈N^*，于是q＝5.当C中恰好含有π和A中2个整数时，C为集合A的好子集，因此z+y+1≥5，z+2≥5；当C中恰好含有π和A中1个整数时，C不是集合A的好子集，因此5>1+z,5>y+z,3≤z<4，又z∈N^*，故z＝3，y≥1且y<2，又y∈N^*，于是y＝1，所以满足条件的数组(q，y，z)＝(5,1,3)．

10．(2008·北京崇文)定义在R上的函数f(x)满足f(x+1)＝－f(x)，且f(x)＝则f(3)＝________.

答案：－1

解析：f(x)满足f(x+1)＝－f(x)，则f(x)＝－f(x+1)＝－[－f(x+2)]＝f(x+2)，则f(x)的周期为2，f(3)＝f(1)＝－1，故填－1.

9．(2008·北京海淀)已知函数f(x)＝

那么不等式f(x)<0的解集为________．

答案：(－∞，－1)∪(－1,1)

解析：由

得x≤0且x≠－1，

由得0<x<1，那么不等式f(x)<0的解集为(－∞，－1)∪(－1,1)，

故填(－∞，－1)∪(－1,1)．

8．(2009·江西五校联考)已知函数f(x)＝

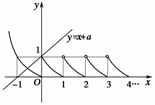
，若方程f(x)＝x+a有且只有两个不相等的实数根，则实数a的取值范围为(　)

A．(－∞，0]　 　　　　　　　　　　　　　　　　　　　　 B．[0,1)

C．(－∞，1)　 　　　　　　　　　　　　　　　　　　　　 D．[0，+∞)

答案：C

解析：函数f(x)的图象如下图所示，从图中可知，当a≥1时，方程f(x)＝x+a只有一个根，当a<1时，满足条件，故选C.